이진 검색트리는 자료를 찾는 색인 역할을 하는 구조다.

레코드와 필드

필드

정보를 나타내는 부분으로 가장 작은 단위의 데이터

레코드

연관되어 있는 필드의 집합

키

다른 레코드와 중복되지 않으면서 레코드를 대표할 수 잇는 필드

검색 트리

분기에 따른 분류

최대 몇 개의 노드로 분리를 할 수 있느냐에 따라 분류할 수 있다.
이진 검색 트리
다중 검색트리

저장 되는 장소에 따른 분류

메인 메모리의 안에 존재하는 지 밖에 존재하는 지에 따라 분류
내부 검색 트리
외부 검색 트리

이진 검색 트리(Binary Search Tree)

특징

• 각 노드는 키 값을 하나씩 갖는다. 각 노드이 키 값은 모두 달라야한다.
• 최상위 레벨에 루트 노드가 있고, 각 노드는 최대 2개의 자식 노드를 가짐
• 임의이 노드의 키 값은 자신의 왼쪽에 있는 모든 노드의 키 값보다 크고, 오른 쪽에 있는 모든 노드의 키값보다 작다.
  

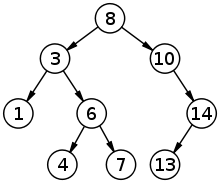
검색

이진트리에서 검색을 하기 위해서는 루트 노드 부터 시작해서 비교를 한다.
현재 노드와 찾기 위한 값을 비교해서 작으면 왼쪽 노드로 이동 크면 오른쪽 노드로 이동한다.

삽입

원소 x를 삽입하기 위해서는 검색 트리에 x를 키 값으로 가진 노드가 없어야 한다.
x에 대한 검색을 실행 후 실패했을 시에 노드의 자식 노드로 삽입한다.
위의 그림에서 8만 있는 노드가 있을 시 3을 삽입하기 위해서는 3을 탐색 한 후 8의 왼쪽에 3이 없기 때문에 3을 8의 자식노드로 삽입한다.

균형

이진 검색트리를 만들 시 균형이 잘 잡혀 트리의 모양을 구현하게 된다면 효율적인 검색을 할 수 있다.
그러나 극단적으로 선형에 가까운 모양으로 데이터가 삽입되면 검색시간이 늘어나는 단점이 있다.

삭제

삭제의 경우는 여러 케이스를 고려해야한다.

삭제할 노드가 리프 노드인 경우

삭제할 노드가 리프 노드일 경우 그냥 삭제만 해주면 된다.

삭제할 노드의 자식 노드가 하나

삭제할 노드의 자식 노드가 하나일 경우에는 노드를 삭제하고 해당 자식 노드를 연결해주는 작업이 필요하다.

삭제할 노드의 자식 노드가 둘

이진 검색트리의 성질을 깨지 않는 원소를 찾아야한다.
이 원소는 왼쪽의 서브 트리 원소보다 크고 오른쪽 서버 트리의 원소보다 작아야하는 원소이다.
해당하는 원소는 다음과 같다.
삭제할 노드의 왼쪽 서브 트리에서 가장 큰 원소
오른쪽 서브트리에서 가장 작은 원소

둘 중 하나를 택해서 삭제할 노드 자리로 위치 시킨다.