📚 DFS

DFS(Depth First Search), 깊이우선탐색은 그래프가 존재할 때 한 경로에 대한 탐색을 끝까지 마치고 다음 경로를 찾는 탐색 방식이다.

백문에 불여일견, 바로 구현해보자.

💻 Implementation

recursive version

class Graph {
	private boolean[][] adj;
	int nodes;
	public Graph(int n) {
		nodes = n;
		adj = new boolean[n][n];
		for (int i=0;i<n;i++)
			for (int j=0;j<n;j++)
				adj[i][j] = false;
	}

	public void createEdge(int a, int b) {
		adj[a][b] = true;
		adj[b][a] = true;
	}

	public void dfs() {
		boolean[] visited = new boolean[nodes];
		for (int i=0;i<nodes;i++)
			visited[i] = false;
		for (int i=0;i<nodes;i++)
			doDfs(visited, i);
	}

	public void doDfs(boolean[] visited, int node) {
		if (visited[node] == false) {
			visited[node] = true;
			System.out.println(node);
			for (int i=0;i<nodes;i++)
				if (adj[node][i] == true)
					doDfs(visited, i);
		}
	}
}

이렇게 재귀적으로 처리해주면 dfs를 간단하게 할 수 있다.

non-recursive version

	public void dfsStack() {
		int node;
		LLStack<Integer> s = new LLStack<Integer>();
		boolean[] visited = new boolean[nodes];
		for (int i=0;i<nodes;i++)
			visited[i] = false;
		for (int i=0;i<nodes;i++) {
			s.push(i);
			while (!s.isEmpty()) {
				node = s.pop();
				if (visited[node] == false) {
					System.out.println(node);
					visited[node] = true;
					for (int j=0;j<nodes;j++)
						if (visited[j] == false && adj[node][j] == true)
							s.push(j);
				}
			}
		}
	}

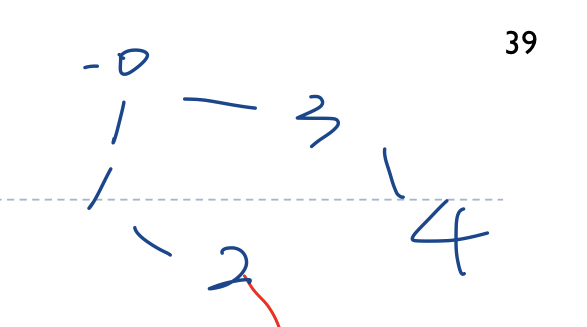
이 그래프에 대해 0에서부터 dfs를 한다면 깊이 우선 탐색이므로 먼저 걸리는 1 경로부터 탐색할 것이다.
그래서 0-1-2-3-4 순서대로 방문할 것.

테스트해보면 실제로 그렇게 나온다.

⌛️ Time Complexity

dfs의 시간복잡도는 ${O(|V|^2)}$ 이다. 인접 행렬로 구현하면 자명하다.
Vertex의 개수만큼 순회하며 doDfs()를 콜하기 때문에 우선 doDFS는 |V|번 호출된다고 볼 수 있다.
그 안에서 간선을 검사하며 |V|번을 다시 순회하기 때문에 |V|번 검사하는 반복문이 총 |V|^2번 실행될 것이고, 비교를 통해 현재 노드를 제외한 vertex를 검사하므로 doDfs는 최악의 경우 |V|*(|V|-1)번 실행될 것이다.

따라서 복잡도는 ${O(|V|^2)}$가 된다.

하지만 노드가 전부 연결된 완전 그래프 수준으로 edge가 많지 않고 인접 리스트로 구현한다면 ${O(|V|+|E|)}$로 잡히는 것이 일반적이다. 이는 간선을 체크할 때 실제로 |V|-1번 수행되는 게 아니라, 간선이 존재할 때만 호출되므로 edge에 대해 2번씩 2|E|번 수행된다. (양쪽 vertex 모두 보기 때문.)