Data Structure
1.[ 자료구조 ] Arrays
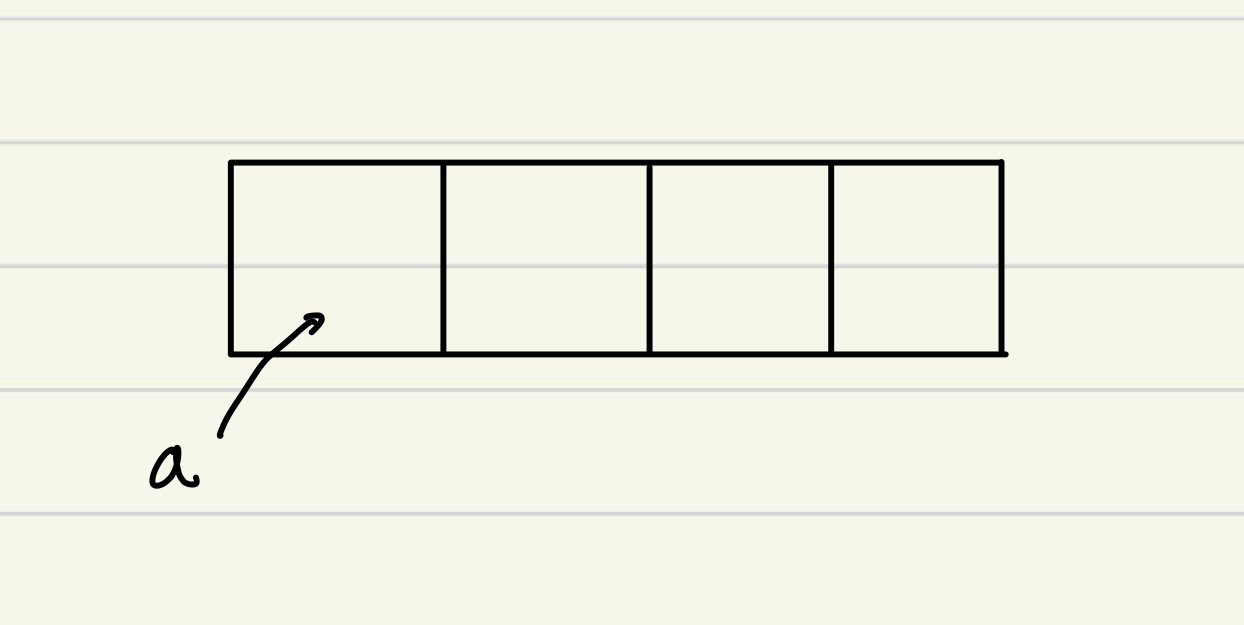
Set of homogenous data. 동일한 자료형으로 구성된 연결된 자료구조이다.C에서도 C++에서도 자바에서도 변수에 어레이를 지정하면 해당 변수는 어레이의 첫 칸 주소 위치를 저장하게 된다.이렇게 선언을 해주면이렇게 메모리 공간에서 연속된 칸을 쓰게 된다.A
2.[ 자료구조 ] Linked List
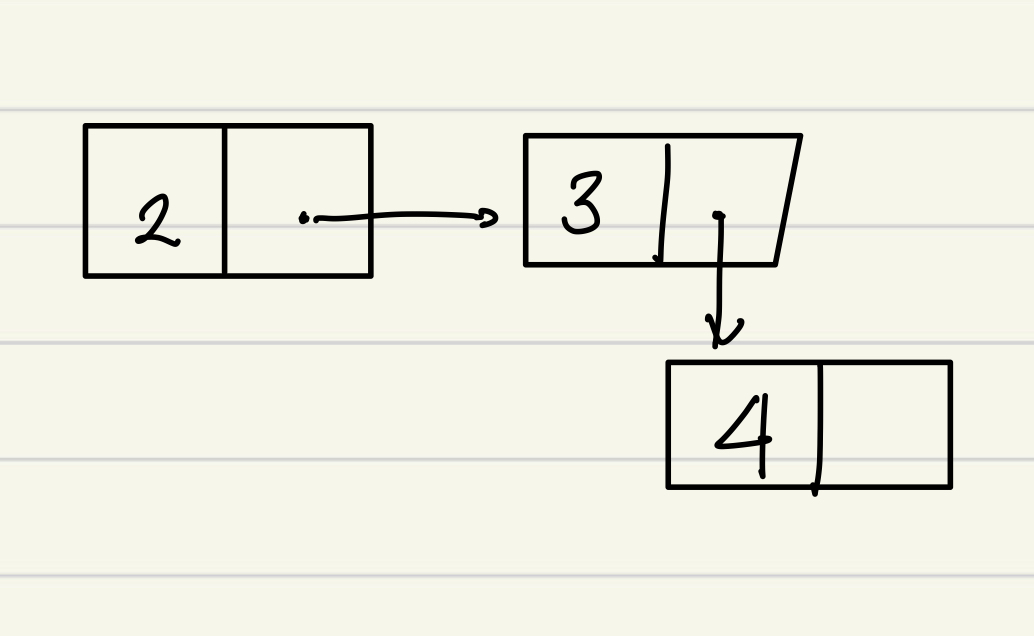
Linked List는 기존 Array의 단점인, '생성 시 크기를 지정해줘야 함' 을 해결하기 위해 고안된 자료구조이다. 저장 공간만 충분하다면 크기가 무한한 리스트를 만들 수 있고, 이를 활용한 다양한 자료구조도 있기 때문에 중요도가 높은 자료구조이다.그림과 같은
3.[ 자료구조 ] Queue
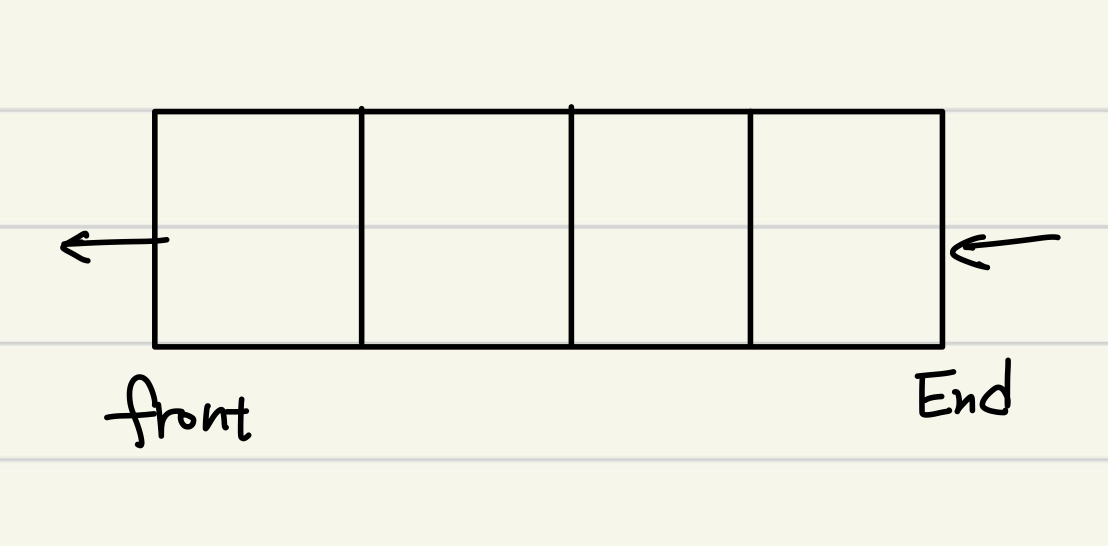
FIFO(First In First Out)이라는 특징을 가지고 있다.Array Representation과 Linked List Representation이 둘 다 가능하다. 기능이 비교적 간단한 편.enqueue : 큐에 요소를 삽입한다.dequeue : 큐의 제일
4.[ 자료구조 ] Stack
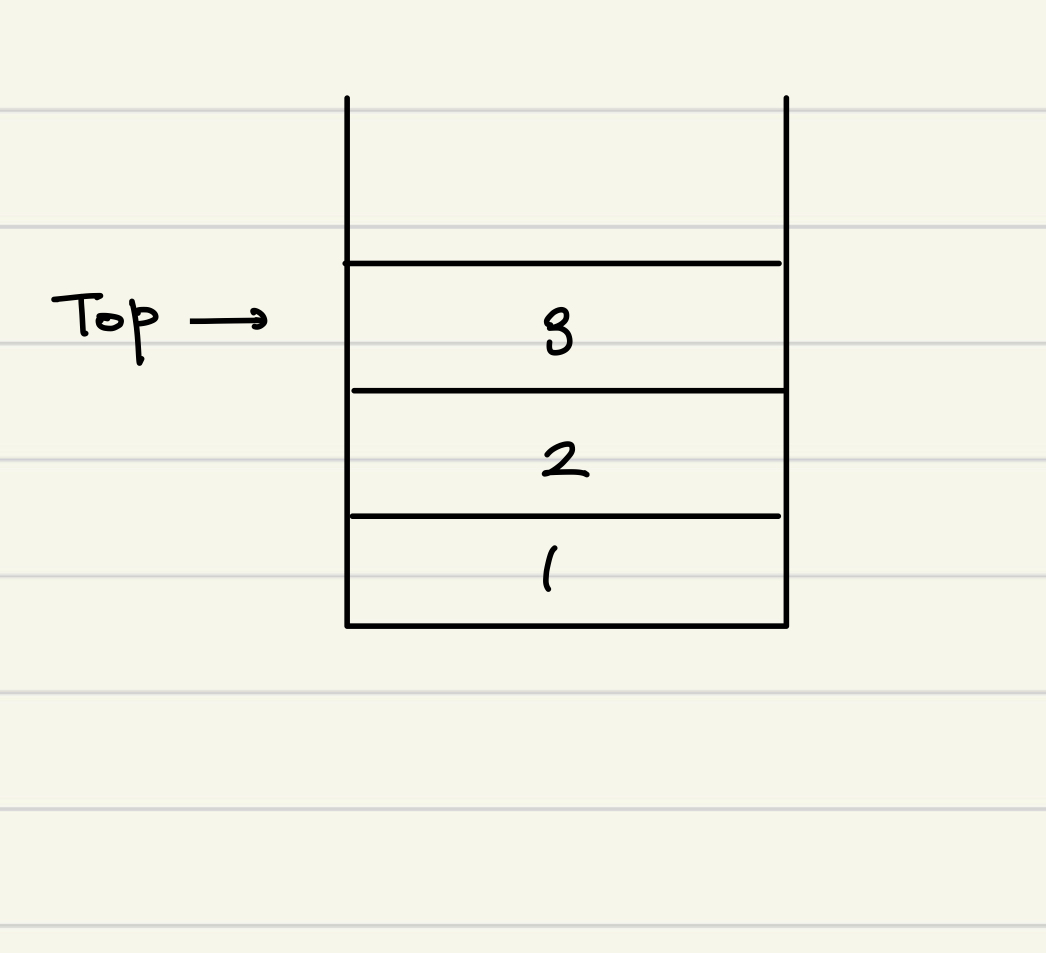
대표적인 LIFO(Last In First Out) 자료구조.한 쪽만 뚫린 상자를 생각하면 편한데, 그러면 먼저 넣은 것은 나중에 나올 수밖에 없기 때문이다.Queue처럼 신경써야 할 게 따로 있지도 않고, 여기저기 요긴하게 쓰이는 녀석이다.push : 스택에 요소를
5.[ 자료구조 ] Bubble Sort

가장 직관적인 정렬 알고리즘이 아닐까 싶다.배열의 앞에서부터 차근차근 올라가면서 바꿔주는 게 거품이 뽀글뽀글 올라오는 것 같다고 해서 붙은 이름.시간복잡도는 O(n^2)이다.리스트의 요소를 처음부터 끝까지 n번 순회하고, 그 안에서도 최대 n-k (k는 상수) 번 순회
6.[ 자료구조 ] Selection Sort

선택 정렬. 대표적인 O(n^2) 정렬 알고리즘 셋 중 하나이다.개념은 그냥 배열을 순회하며 최솟값을 찾아 앞에서부터 채워나간다.머.. 간단하다. O(n^2). 하지만 Bubble, Insertion, Selection 세 정렬 알고리즘 중에 평균적으로 가장 오랜 시간
7.[ 자료구조 ] Insertion Sort

삽입 정렬.정렬할 값 기준 왼쪽의 리스트가 정렬되어 있다고 가정하고, 그 속에서 들어가야 할 값을 찾는 정렬이다.O(n^2). 순회가 두 번이기 때문! 각 순회는 최대 N, N-1번이므로 N^2가 된다.
8.[ 자료구조 ] Recursion
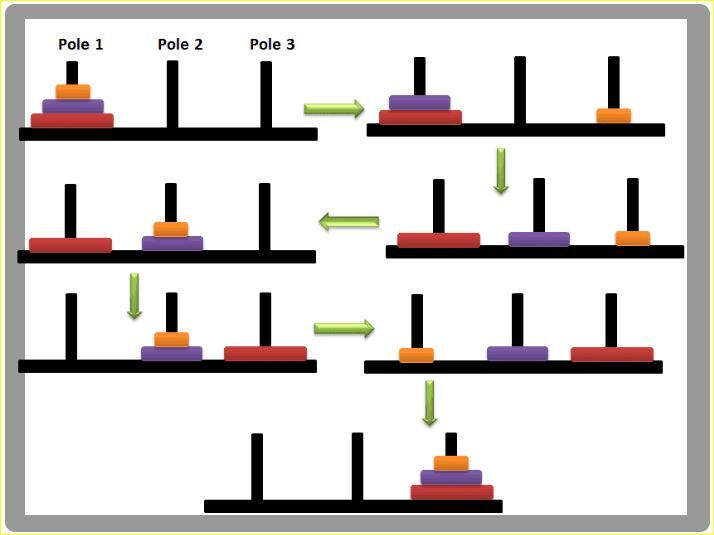
다시 재, 돌아올 귀. 자기 자신을 호출하는 함수를 뜻한다.재귀를 구현할 때 주의해야 하는 점은 breakPoint로 작용할 base case를 잘 지정하지 않으면 무한루프에 빠진다. 또 문제를 작게 쪼개서 생각해야 구현하기 편한 것 같다.재귀의 대표적인 예. 작은 원
9.[ 자료구조 ] Quick Sort

Top-Down 재귀적 알고리즘을 이용하는 정렬 방법.피벗 값을 기준으로 왼쪽과 오른쪽을 약하게 정렬된 상태로 만들고 재귀적으로 내려가면서 정렬을 완료한다. 이 떄 리스트의 왼쪽에는 피벗 값보다 작은 값만 나타나도록 하고, 오른쪽에는 피벗 값보다 큰 값만 나타나도록 한
10.[ 자료구조 ] merge sort
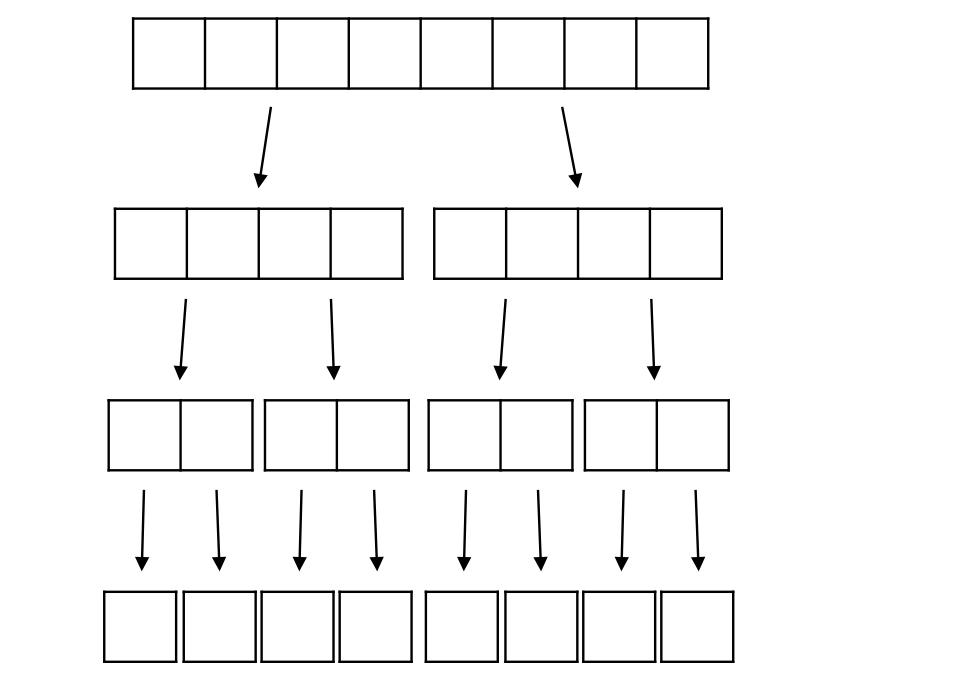
Quick Sort가 Top-down Approach였다면 Merge Sort는 Bottom-up Approach이다. 리스트를 하나가 남을 때까지 반으로 계속 쪼개고, 더이상 쪼갤 수 없을 때 비교를 통해서 정렬된 리스트를 만든다고 생각하면 된다.n만큼의 추가 공간이
11.[ 자료구조 ] Radix Sort

Radix Sort(기수 정렬) 이란 배열이 모두 같은 자릿수의 정수로 이루어져있을 때, 각 자리수를 비교해서 정렬하여 최종적으로 모든 자릿수가 정렬되도록 하는 방법이다.개념은 0부터 9까지 각 자릿수를 담을 큐의 배열을 만들고, 각각의 큐에 해당 자릿수에 맞는 요소를
12.[ 자료구조 ] Tree와 Binary Tree
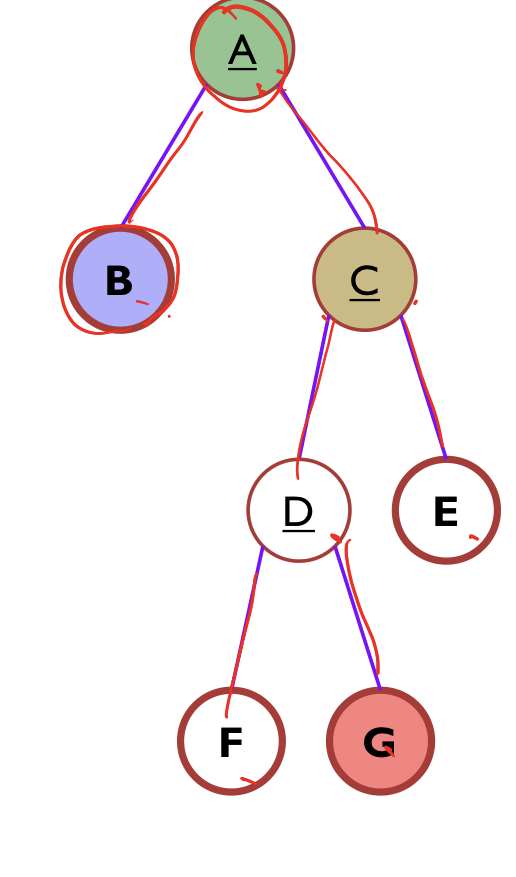
트리는 자료구조의 일종으로, root에서부터 자식들이 뻗어나가는 모습이 나무와 닮아 붙은 이름이다. 대표적으로 이진 트리 (자식이 2개인 트리) 가 유명하다.하나 이상의 유한한 노드의 집합root 노드라는 식별 가능한 노드가 있다 (최상위 노드)나머지 노드도 ${T}\
13.[ 자료구조 ] Binary Search Tree
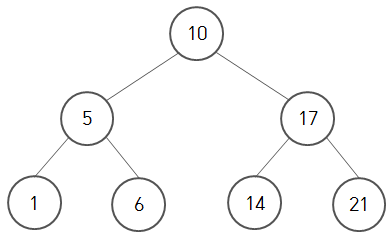
Binary Search Tree(이진탐색트리) 란 다음과 같이 정의된다.빈 트리 혹은 아래 사항을 만족하는 Binary Treeroot가 키값을 가지고 있다고 하면 왼쪽 subtree의 값은 모두 key보다 작고, 오른쪽은 큰 Binary Tree양쪽 Subtree
14.[ 자료구조 ] Heap

힙이란 각 노드의 값이 child의 그것보다 작다는 원칙을 지키는 Complete binary tree이다. 그런 만큼 왼쪽부터 값이 이쁘게 들어가게 된다.보통 Array로 구현하므로 본인도 Array 구현을 진행해보겠다.이 때는 array의 0번째 칸은 쓰지 않고 1
15.[ 자료구조 ] Heap Sort

힙 정렬은 앞서 소개한 자료구조인 Heap의 성질을 이용해서 배열을 정렬하는 방법이다.Heap의 Array representation을 봤을 때, 삭제 후에도 요소는 배열에 남아있지만 뒤에서부터 차곡차곡 쌓이게 된다.이러한 성질을 이용해서 배열을 힙으로 만들고, 반복
16.[ 자료구조 ] Graph
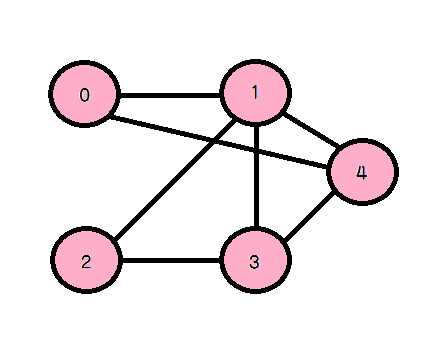
노드와 간선으로 이루어져 있는 자료구조. 그래프 G=(V,E) 는유한한 공집합이 아닌 Vertex의 집합 V와서로 다른 Vertices의 쌍인 Edge의 집합 E로 이루어진다.adjacent : 두 Vertex가 Edge로 연결되어 있으면 adjacent하다.incid
17.[ 자료구조 ] DFS
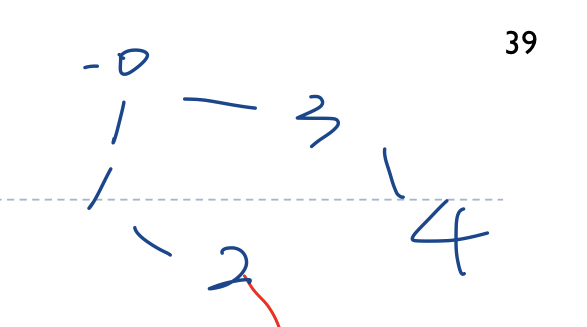
DFS(Depth First Search), 깊이우선탐색은 그래프가 존재할 때 한 경로에 대한 탐색을 끝까지 마치고 다음 경로를 찾는 탐색 방식이다.백문에 불여일견, 바로 구현해보자.이렇게 재귀적으로 처리해주면 dfs를 간단하게 할 수 있다.이 그래프에 대해 0에서부터
18.[ 자료구조 ] BFS
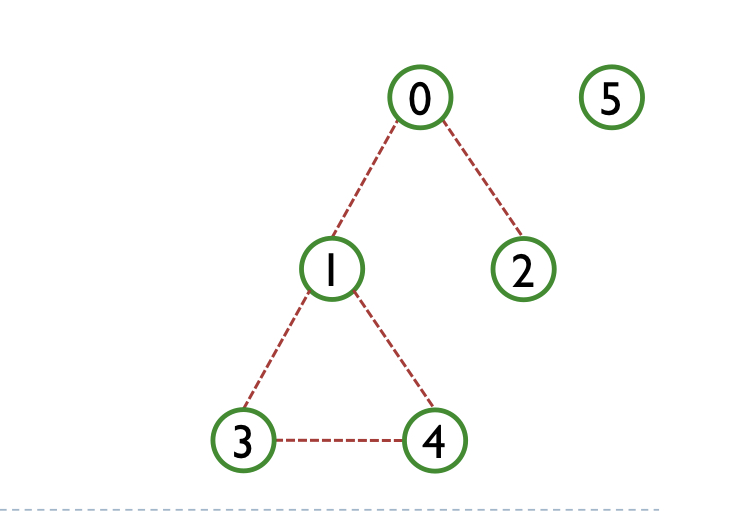
BFS (Breadth-First-Search), 너비우선탐색은 앞서 소개한 DFS와 다르게 한 레벨 한 레벨씩 탐색해나가는 과정이다.재귀로 할 수도 있지만, 큐를 이용해서 간단하게 구현할 수 있다.이렇게 큐를 이용해서 넘겨주면 된다.그래프가 이런 모양이라면 bfs 시
19.[ 자료구조 ] Kruskal's Algorithm

MST(최소신장트리) 란 가중치가 주어진 그래프에서 가중치의 합을 최소로 하는 spanning tree를 말한다.다음 세 가지 명제 중 두 개가 참이면 나머지 하나도 참이다.그래프가 연결되어 있다.그래프가 acyclic하다.그래프가 |V|-1개의 간선만을 가진다.크루스