📚 재귀
다시 재, 돌아올 귀. 자기 자신을 호출하는 함수를 뜻한다.
재귀를 구현할 때 주의해야 하는 점은 breakPoint로 작용할 base case를 잘 지정하지 않으면 무한루프에 빠진다. 또 문제를 작게 쪼개서 생각해야 구현하기 편한 것 같다.
💻 예제
하노이의 탑
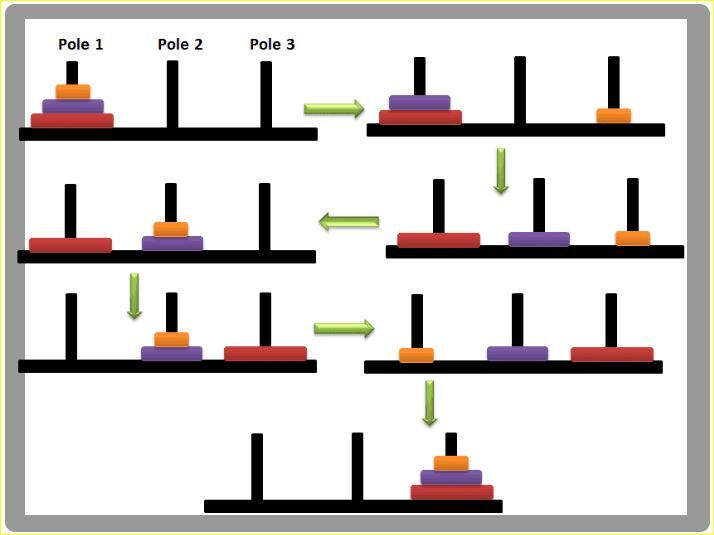
재귀의 대표적인 예.
작은 원판이 큰 원판 아래로 들어갈 수 없다고 할 때, 다른 기둥으로 전체 탑을 옮기는 데 드는 최소 이동횟수를 구하는 문제이다.
위의 그림처럼 원판 3개의 경우를 생각해보자. 3번 기둥으로 옮겨야 할 때, 처음에 1-3으로 가장 작은 원판을 옮기고, 1-2로 중간 원판을 옮긴다. 다시 3-2로 작은 원판을 옮기고, 1-3으로 가장 큰 원판을 옮겨준 다음에 2-1로 작은 원판을, 2-3으로 중간 원판을, 1-3으로 작은 원판을 옮겨주면 된다.
벌써 머리가 아프다. 간단하게 할 방법이 없을까?
원판이 두 개만 있을 때를 생각해보자.
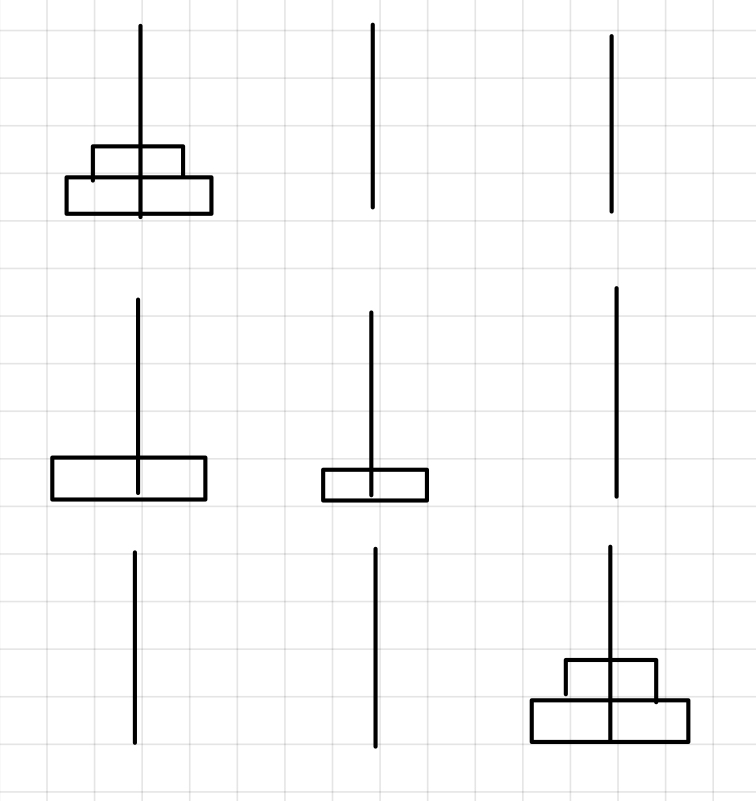
간단하게 하나를 보조 기둥 (목적지가 아닌 기둥) 으로 옮기고, 가장 큰 원판을 목표 기둥으로 옮겨주면 된다.
여기서 조금만 더 생각해본다면 원판이 세 개인 케이스도 크게 다르지 않다는 것을 알 수 있다.
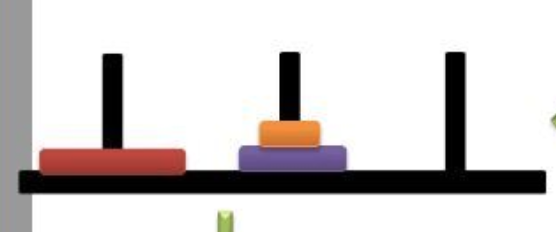
결국 이러한 형태가 되어야 전체 원판을 옮길 수 있기 때문. 이거를 n으로 일반화시켜보면
1) 먼저 n-1개의 원판을 보조 기둥으로 옮겨야 한다.
2) 1개를 목적지로 옮긴다.
3) 다시 n-1개를 보조 기둥에서 목적지로 옮긴다.
한 번 코드로 구현해보자.
class Hanoi {
public static void main(String[] args) {
int n = 3;
Hanoi(1, 3, n);
}
public static void Hanoi(int start, int end, int n) {
int aux;
if (n <= 0) return ;
aux = 6-(start+end);
Hanoi(start, aux, n-1);
System.out.println(start + " to " + end);
Hanoi(aux, end, n-1);
}
}
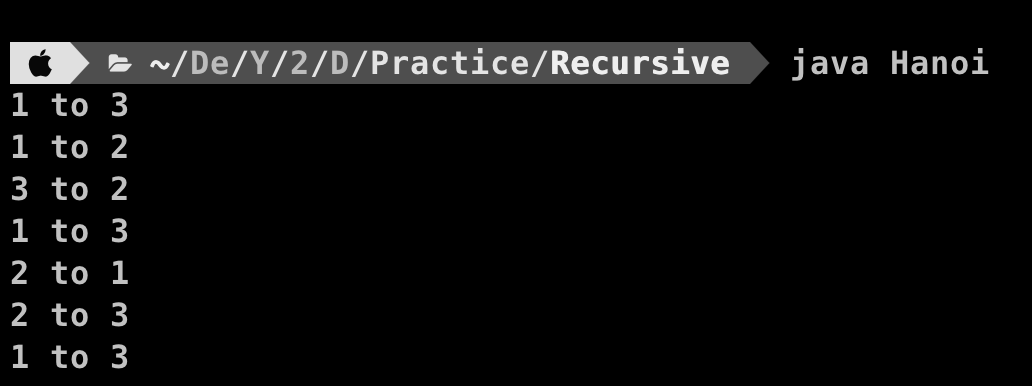
잘 되는 것을 볼 수 있다.
이항계수 구하기
이항 계수란 이항식을 이항 정리로 전개했을 시 각 항의 계수이다. 조합 공식과도 동일하다.
이항 계수의 점화식은 다음처럼 쓸 수 있다.
그리고 이므로
n과 k의 계수만 알면 공식 필요없이 계산을 할 수 있다.
class Binomial {
public static void main(String[] args) {
int n = 9;
int k = 3;
System.out.println(binomial(n,k));
}
public static int binomial(int n, int k) {
if (n == k || k < 1) return 1;
return (binomial(n-1, k) + binomial(n-1, k-1));
}
}간단하다 ! 그냥 Base case에 대한 계산만 해주고 n과 k를 깎아가면서 함수에 넣기만 해주면 된다.
😵💫 Stack을 이용한 재귀의 표현
사실 재귀의 경우, 시간복잡도가 최악으로 치닫는 경우가 많다. 애초에 단순 반복을 통해 문제해결이 어려울 때 사용하는 것이기도 하고, 데이터의 양도 많아지기 때문. 그렇기에 후입선출의 특성을 가진 Stack을 이용해서 재귀 기능을 구현할 수 있다.
이게 가능한 것은 사실 재귀 자체도 함수의 Call Stack의 원리에서부터 도출되기 때문. 대표적으로 자바의 Call Stack은 아래처럼 구현된다.
main에서 firstMethod를 수행하고, firstMethod에서 secondMethod를, secondMethod에서 println을 수행한 스택이다.
차례대로 스택에 들어가고, 후입된 함수부터 실행되고 차례대로 빠져나온다.
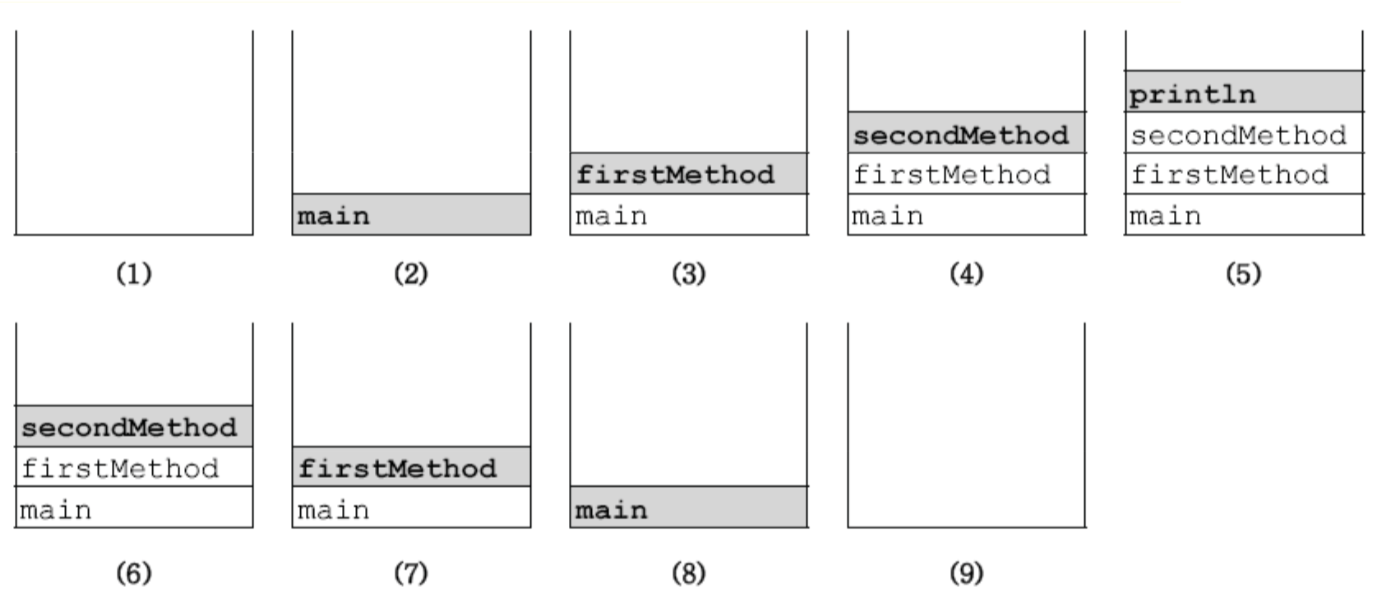
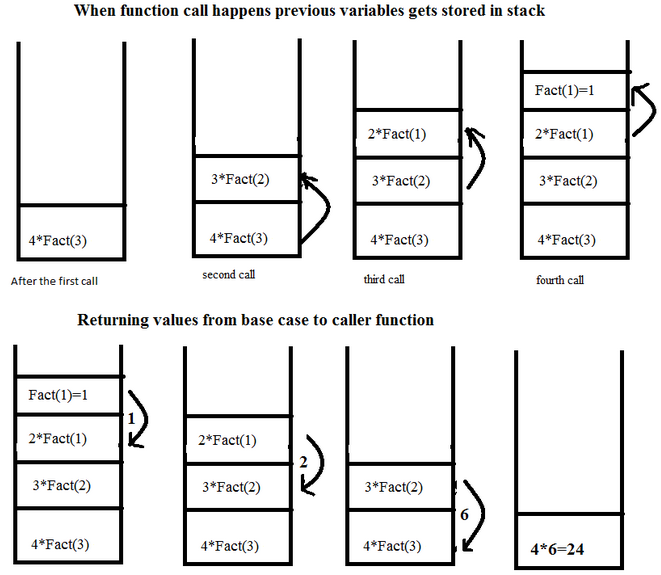
재귀의 경우 이렇게 돌아가야 할 주소 데이터와 변수 데이터를 담은 실질적으로는 각각 다른 함수가 스택에 쌓이게 되고, 이를 계산하면서 돌아오는 것이다.
하노이 재귀의 스택 표현
우선 재귀를 스택으로 표현하기 위해, 특정 함수의 진행상황과 데이터를 담고 있는 Context란 클래스를 만들어보자.
class Context {
public int n, from, to;
public int process;
public Context(int n, int f, int t, int w) {
this.n = n;
from = f;
to = t;
process = w;
}
}
Context는 기존 Hanoi 함수의 재귀 콜을 흉내낼 것으로 원판의 개수 n, 시작 기둥 from, 도착 기둥 end를 들고 있을 것이다. 추가로 process라는 변수가 있는데, 얘는 기존 재귀 Hanoi에서 현재 함수가 몇 번째 Hanoi 호출까지 진행되었는지 확인할 수 있는 변수이다.
기존 Hanoi 함수는 다음과 같다.
public static void Hanoi(int start, int end, int n) {
int aux;
if (n <= 0) return ; // whereToReturn = 0
aux = 6-(start+end);
Hanoi(start, aux, n-1); // whereToReturn = 1
System.out.println(start + " to " + end);
Hanoi(aux, end, n-1); // whereToReturn = 2
}n<=0인 케이스에서 한 번 검사를 해줘야 한다. 현재 함수가 계속 진행되어야 하는지 말아야 하는지. 만약 진행되어야 한다면 Stack에 1) 복귀해야 할 위치를 담은 Context, 2) 실행해야 할 다음 Context를 넣어준다.
복잡하지만 각 Hanoi의 호출을 0, 1, 2로 보면 된다. 0의 경우 Hanoi를 호출하기 전, 1은 Hanoi의 첫 번째 호출, 2는 Hanoi의 두 번째 호출.
그래서 0의 경우에는 n이 0보다 큰지 검사를 하고 만약 그렇다면 다음으로 진행해주면 된다. 그런 경우 현재 Context의 process를 1 증가시켜 주고, n-1개를 from에서 aux로 이동시키는 Context를 새로 push해주면 된다.
그래서 첫 호출에서는 다음과 같은 모양이 될 것이다.
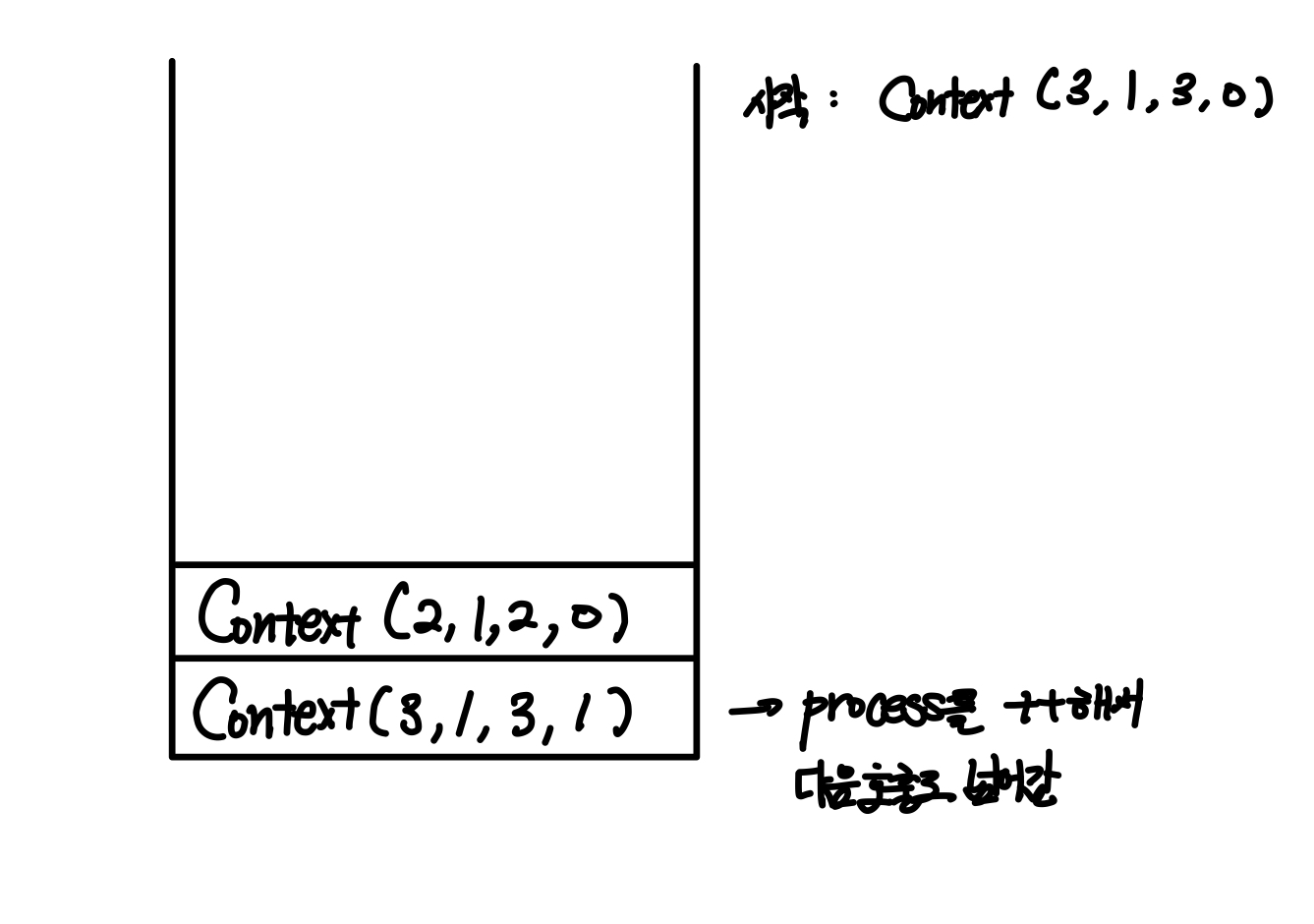
그러면 다음 Context는 peek()을 통해 n=2, from=1, to=2, process=0인 녀석이 될 것이다. 동일하게 진행해주면 된다.
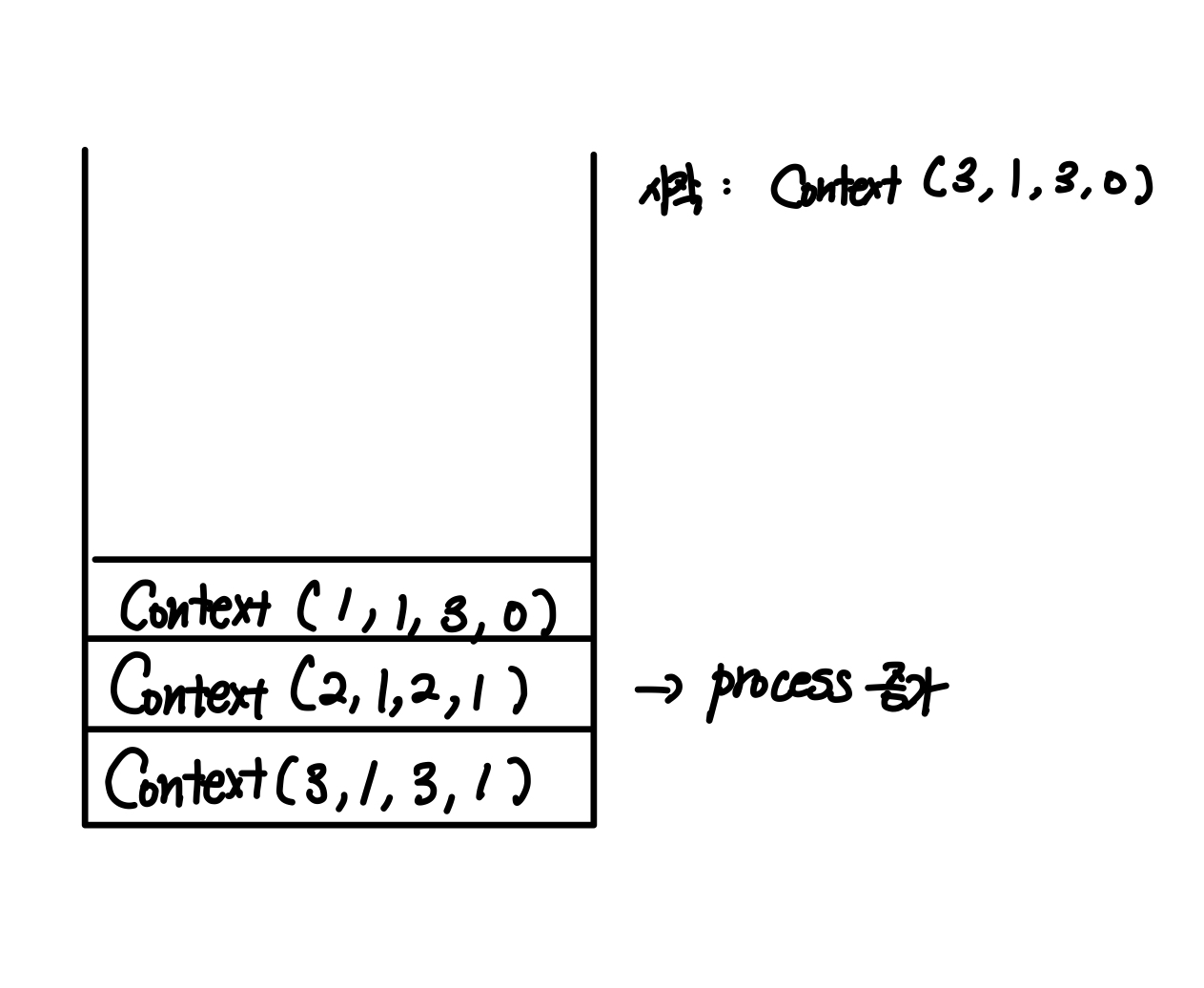
이제 첫 번째 n=0인 케이스가 나오게 된다.
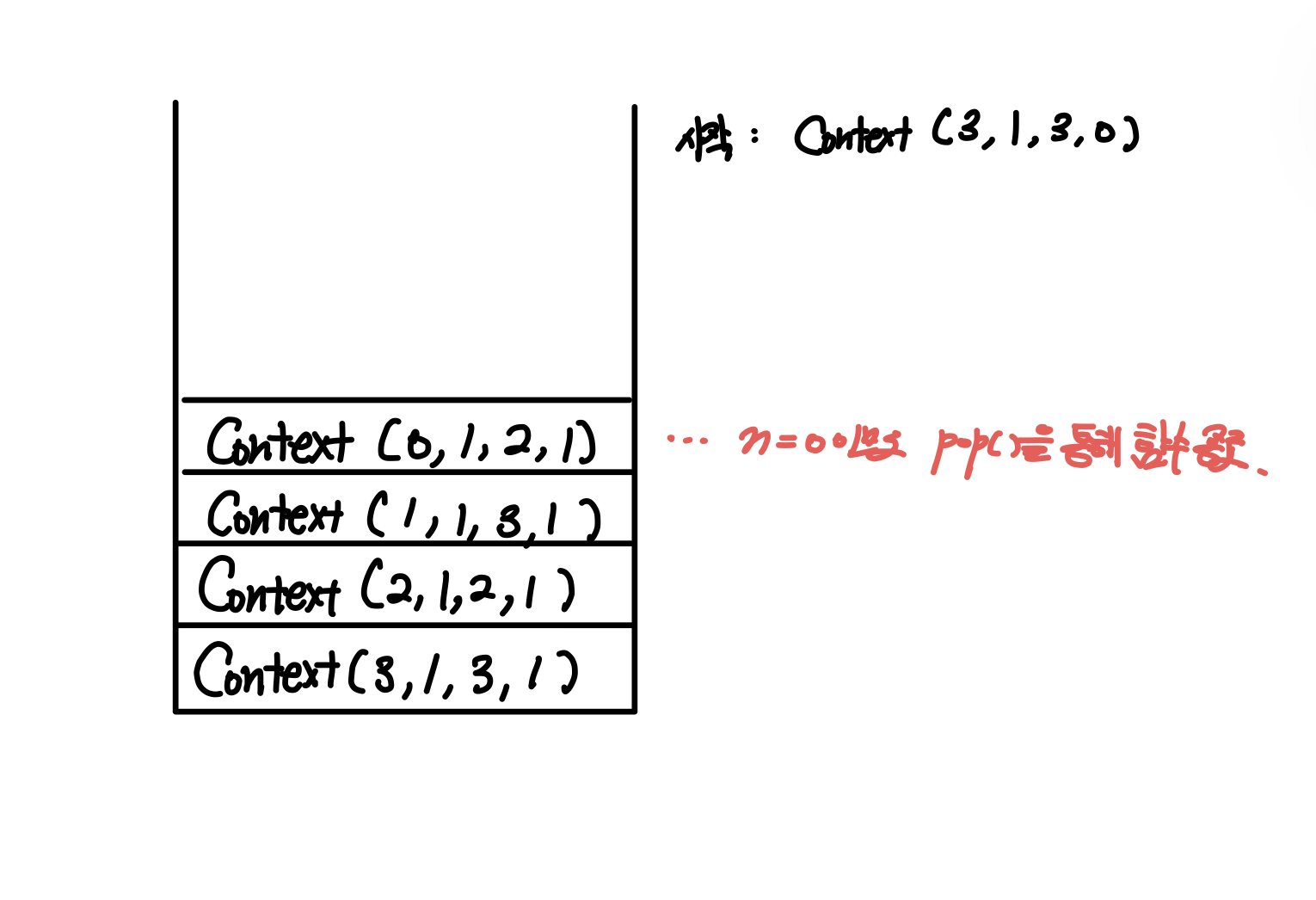
그러면 해당 함수는 더이상 진행되면 안되므로 pop()을 통해 함수 스택에서 제거해준다.
그리고 다음 Context는 다시 Context(1, 1, 3, 1)이 되는데, 이 경우 process를 2로 늘려주고 원래 함수처럼 "from to to"를 출력해준 다음에, 원래 함수에서 두 번째 Hanoi 호출이었던 Hanoi(n-1, aux, to)를 흉내내서 Context(n-1, aux, to, 0)을 push해준다.
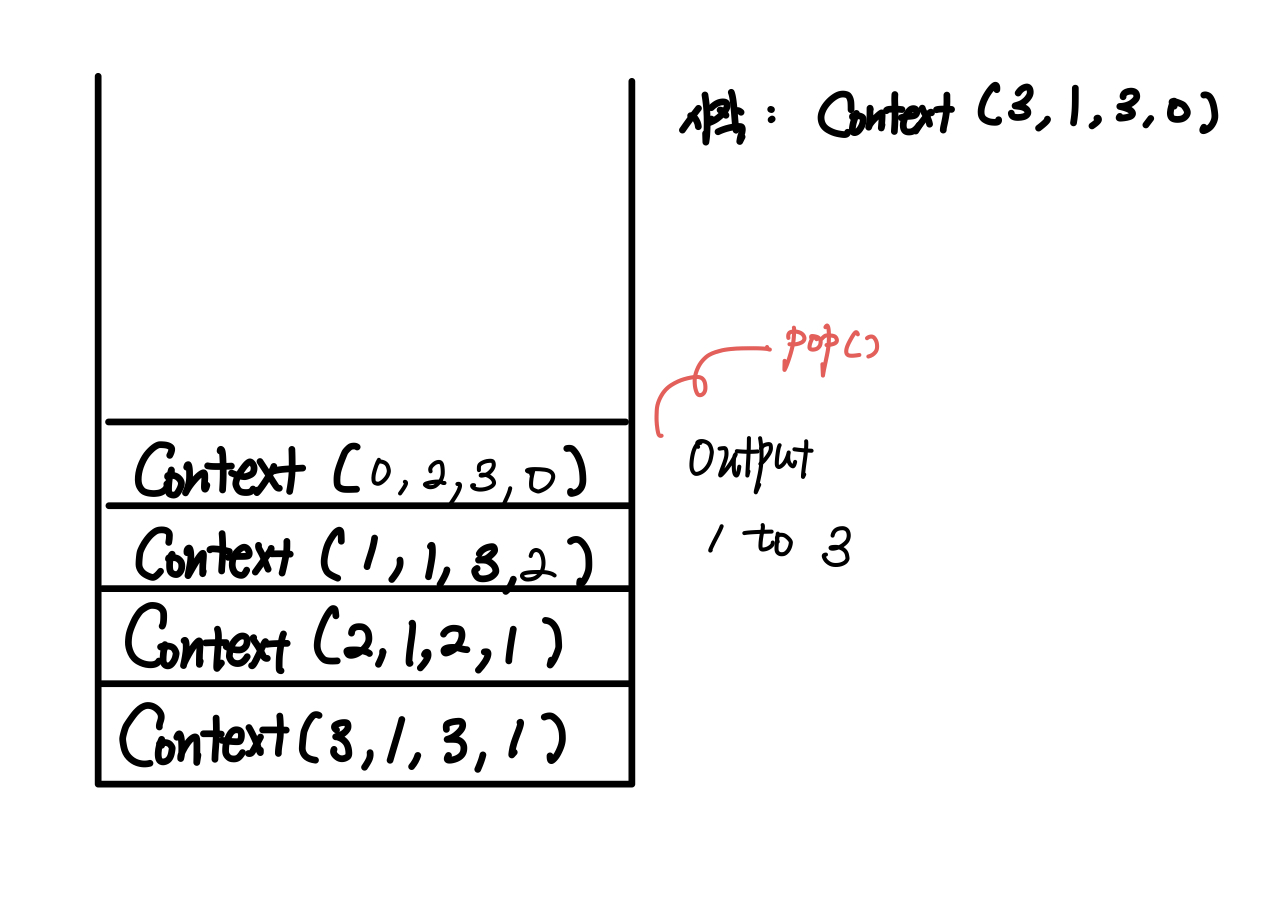
그러면 다시 0,2,3,0의 Context가 push될 것이고 바로 pop된다.
다음은 Context(1,1,3,2)가 되는데, 얘는 Hanoi의 2번째 호출까지 무사히 마쳤으므로 pop()을 해준다.
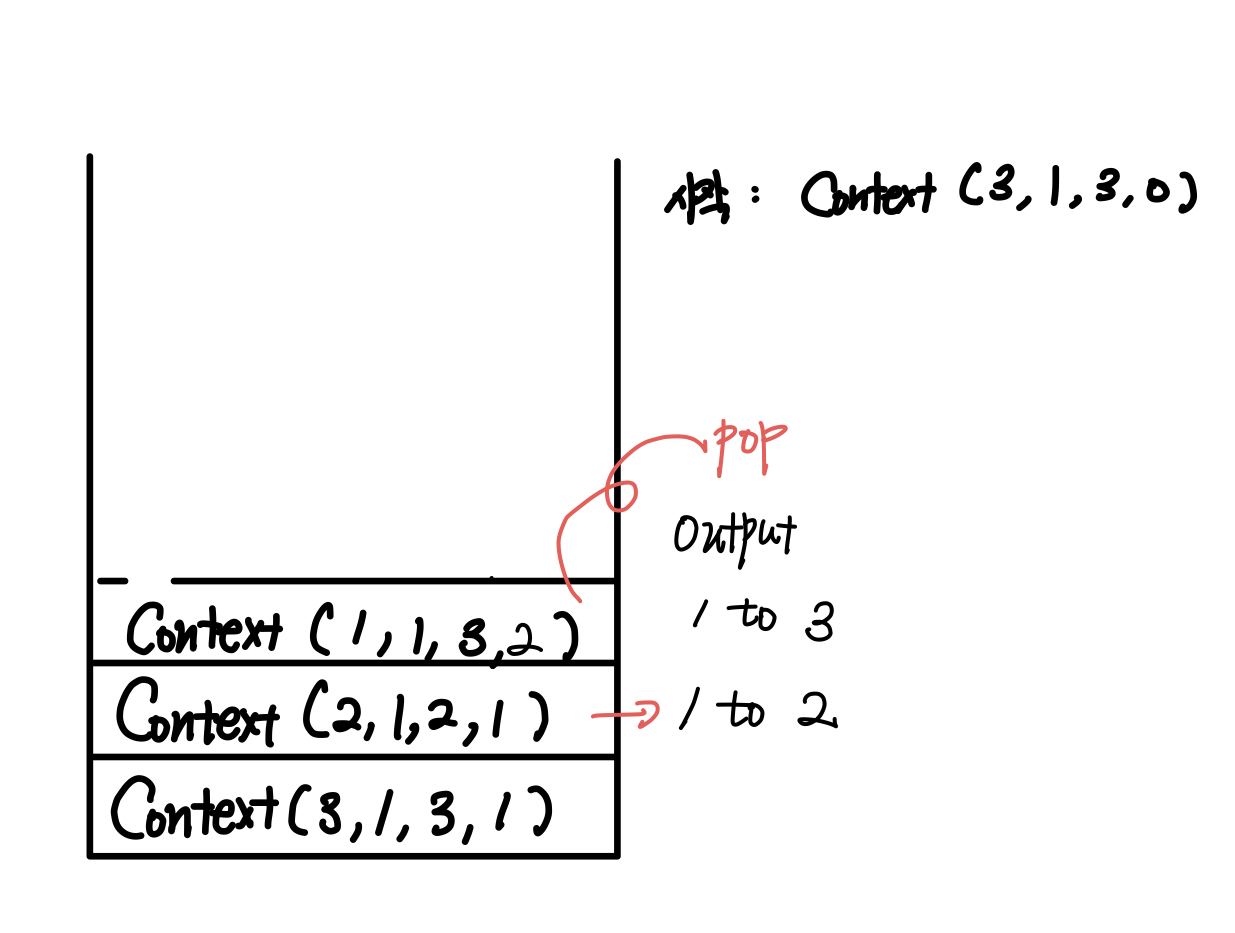
이런 식으로 반복해서 진행해주면 함수의 Call Stack의 동작을 재현할 수 있다.
public static void Hanoi(int n, int from, int to) {
LLStack<Context> s = new LLStack<Context>();
Context ctx;
boolean calldone;
ctx = new Context(n, from, to, 0);
s.push(ctx);
while (ctx != null) {
switch (ctx.process) {
case 0:
if (ctx.n > 0) {
ctx.process++;
s.push(new Context(ctx.n-1, ctx.from, 6-(ctx.from+ctx.to), 0));
} else
s.pop();
break ;
case 1:
System.out.println(ctx.from + " to " + ctx.to);
ctx.process++;
s.push(new Context(ctx.n-1, 6-(ctx.from+ctx.to), ctx.to, 0));
break ;
case 2:
s.pop();
break;
}
ctx = s.peek();
}
}
