📚 Merge Sort

Quick Sort가 Top-down Approach였다면 Merge Sort는 Bottom-up Approach이다. 리스트를 하나가 남을 때까지 반으로 계속 쪼개고, 더이상 쪼갤 수 없을 때 비교를 통해서 정렬된 리스트를 만든다고 생각하면 된다.
n만큼의 추가 공간이 필요하다는 점이 특징. 물론 in-place 구현도 가능하다고는 하는데, 굉장히 복잡해진다고 한다.

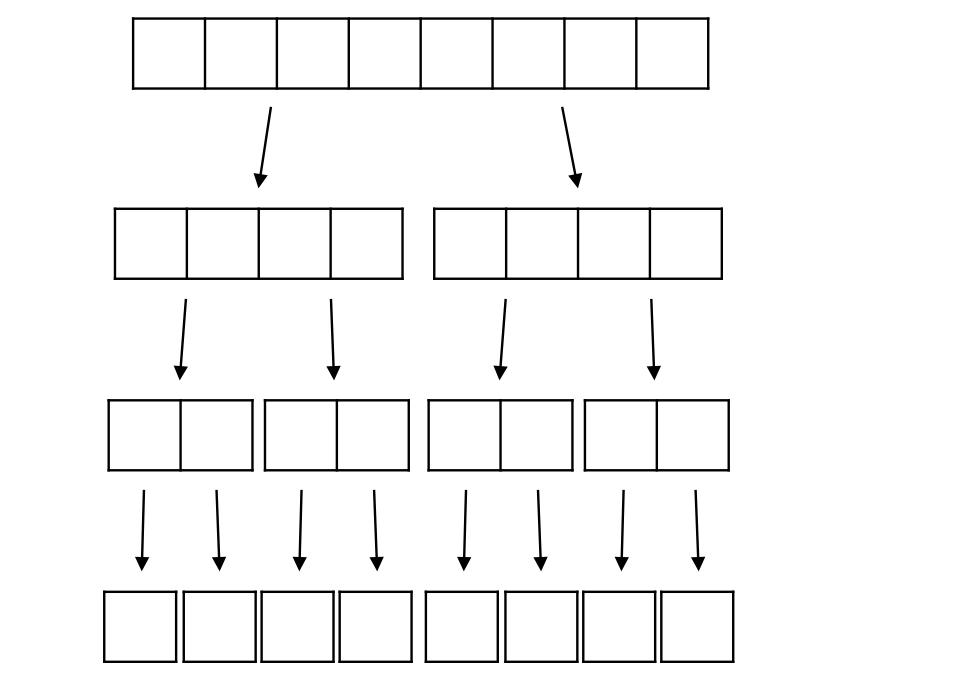
Merging

두 배열이 있을 때 둘을 합쳐 정렬된 배열을 만들려면 어떻게 해야 할까?
단순히 생각하면 그냥 하나씩 비교하면서 둘의 크기를 합친 크기를 가진 배열에 넣으면 된다.
merge sort는 이 개념을 이용하기 때문에 Merge sort라고 불린다.

💻 Implementation

class MergeSort {
	public static void main(String[] args) {
		int[] arr = {8, 1, 5, 3, 2, 4};
		mergeSort(arr);
		for (int i=0;i<6;i++) System.out.print(arr[i] + " ");
	}

	public static void mergeSort(int[] arr) {
    // Merge 결과를 저장할 추가공간
		int[] aux = new int[arr.length];

		doMergeSort(arr, 0, arr.length-1, aux);
	}

	public static void doMergeSort(int[] arr, int start, int end, int[] aux) {
    // 한 칸의 배열이면 비교할 게 없음
		if (start >= end) return;
        // 반으로 쪼갤 인덱스
		int mid = (start + end)/2;

// 반씩 나눠 mergesort 실행
		doMergeSort(arr, start, mid, aux);
		doMergeSort(arr, mid+1, end, aux);

		int i,j,k;
		i = k = start;
		j = mid+1;

// merge 실행 : start에서 end까지 작은 것부터 차례대로 aux에 넣음
		while (i<=mid && j<=end) {
			if (arr[i] <= arr[j])
				aux[k++] = arr[i++];
			else
				aux[k++] = arr[j++];
		}
        // 남은 요소 넣기
		while (i<=mid)
			aux[k++] = arr[i++];
		while (j<=end)
			aux[k++] = arr[j++];
		// 원래 Array에 정렬된 요소 복사
        for (i=start;i<=end;i++)
			arr[i] = aux[i];
	}
}

⌛️ Time & Auxiliary Complexity

Time Comp

시간은 O(nlogn) 복잡도를 가진다.
배열을 반으로 계속해서 쪼개기 때문에 logn번 분할이 일어나고, 각 분할에서 n번의 비교를 하기 때문.

Auxiliary

공간은 O(n) 복잡도를 가진다. 당연히 배열 하나를 추가로 만들기 때문.

Is this stable?

Merge Sort는 stable하다. 다만 왼쪽 리스트부터 mergeSort를 실행하고, 병합 때도 왼쪽 요소부터 합치도록 유의한다면 stable하다.
두 요소를 비교하고 합칠 때 값이 같다면 왼쪽 리스트에서 온 것을 먼저 넣어줘야 하므로,

if (arr[i] <= arr[j])
	aux[k++] = arr[i++]

이 부분만 지켜주면 된다.