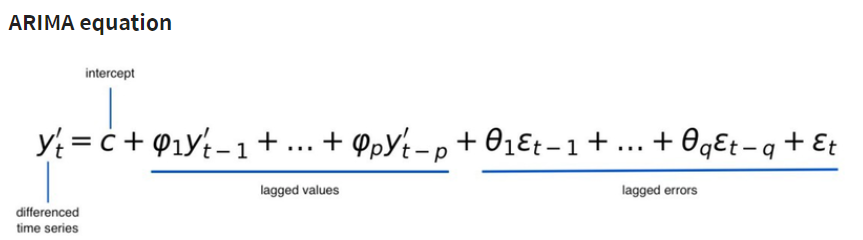ARIMA
AR : AutoRegressive Model(자기 회귀)
과거가 미래를 예측한다는 사실에 의존하는 모델
특정 시점 t의 값은 이전 시점을 구성하는 값들의 함수
I : Integration(차분)
MA : Moving Average Model(이동 평균)
각 시점의 데이터가 최근의 과거 값에 대한 오차로 구성된 함수
과거의 오차가 현재의 과정에 영향을 미침
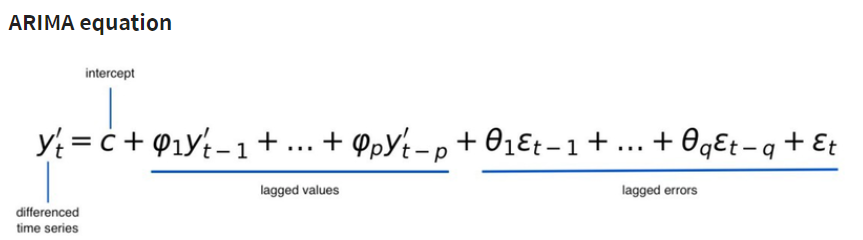
p : AR lagged values
d : 차분의 개수
q : MA lagged errors
Parameter tune
박스-젠킨스 방법
1. 시각화 및 도메인 지식을 통해 초기 파라미터(p, d, q) 추정
2. 모델 적합 후 시각화 및 성능 평가 수행
3. 부적합할 경우 파라미터 조정
Auto-Arima
Log like lihood를 이용한 Step-wise방법
해당 방법은 Overfitting의 가능성 존재
차분(d)이 2를 넘어가면 Overfitting으로 봄, AR(p), MA(q)도 3을 넘기지 않는 것이 바람직함
Other Arima
SARIMA
ARIMA + Seasonality = ARIMA모델에 계절성 요소 추가
(p, d, q) / M(P, D, Q)
계절성이 있는 데이터도 모델링 가능
ARIMAX
ARIMA + Time Series Regression = ARIMAX
ARIMA에 외부 변수를 추가함
ARIMA 모델링
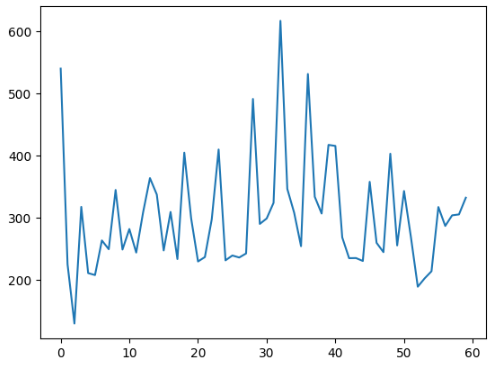
데이터 불러오기
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima.model import ARIMA
df = pd.read_csv('/content/drive/MyDrive/DataSet/Aiffel/Daily_Demand_Forecasting_Orders.csv', delimiter=';')
data = df['Target (Total orders)']
plt.plot(data)
plt.show()
ACF
plot_acf(data)
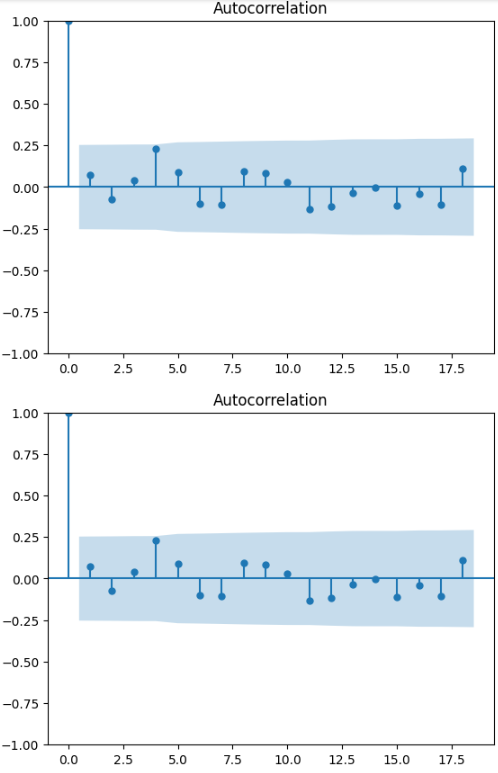
파란 네모 박스에서 벗어난 데이터가 존재하지 않음
=> 유의미한 데이터가 존재하지 않음
PACF
plot_pacf(data)
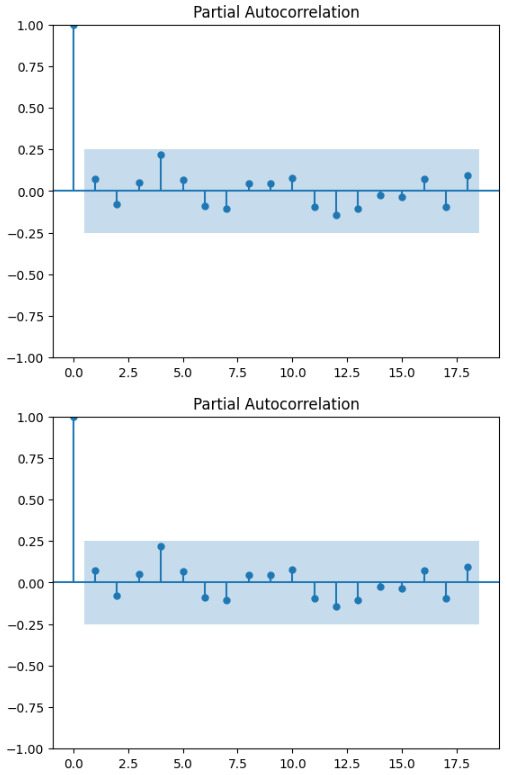
파란 네모 박스에서 벗어난 데이터가 존재하지 않음
=> 유의미한 데이터가 존재하지 않음
Modeling
model1 = ARIMA(data, order=(1,0,0))
model2 = ARIMA(data, order=(0,0,1))
model3 = ARIMA(data, order=(1,0,1))
res1 = model1.fit()
res2 = model2.fit()
res3 = model3.fit()
print(res2.summary())
p : AR lagged values
d : 차분의 개수
q : MA lagged errors
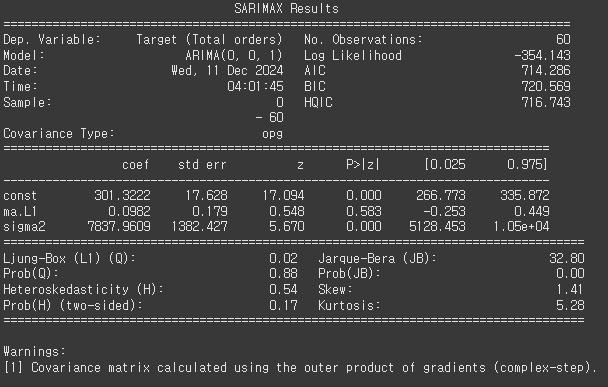
2번째 모델이 제일 성능(Log Likelihood, AIC, BIC)이 좋게 나옴
예측 결과 시각화
predictions = res2.fittedvalues
plt.figure()
plt.plot(data)
plt.plot(predictions)
plt.show()
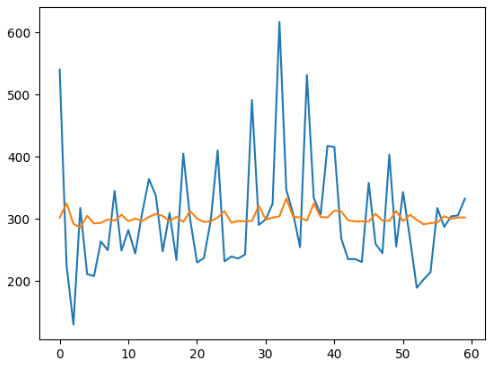
주황색이 예측한 값인데 전혀 비슷하지 않음
Auto Arima
Auto Arima를 통해 파라미터 튜닝
model = pm.AutoARIMA(seasonal=False, stepwise=True, suppress_warnings=True, trace=True)
res = model.fit(data)
print(res.summary())
seasonal : 계절성 고려 여부(True : SARIMA / False : ARIMA)
stepwise : 파라미터 튜닝 방법
- True : 순차적으로 최적의 모델을 선택하며 AIC or BIC기준으로 모델을 최적화함
- False : 그리드 탐색방법을 이용하여 가능한 모든 조합을 이용하여 모델을 최적화함
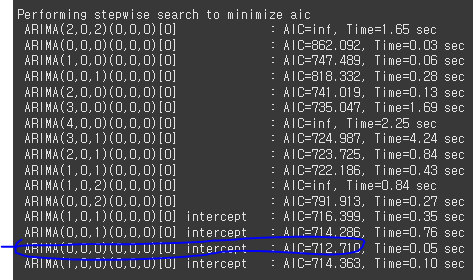
최적의 모델은 ARIMA(0, 0, 0)으로 확인됨
=> ARIMA(0, 0, 0)은 백색잡음으로 시계열을 이용한 의미 있는 예측이 불가능한 상황을 뜻함