1. Interpreting ML Model
높은 성능을 가지는 모델을 만들기 위해 랜덤포레스트, 부스팅과 같은 복잡도가 높은 모델을 사용하게 된다. 이처럼 복잡한 계산으로 인해 내부 작동원리가 드러나지 않는 모델들을 Black Box Model이라 한다. 이러한 블랙박스 모델들을 해석하는 방법에 대해 정리하였다.
1.1 모델을 왜 해석해야 하는가?
많은 분야에서 모델을 무조건 신뢰할 수 없다.
- 의료 분야, 자율자동차, 금융 분야 등 모델에 따라 위험성이 큰 분야에서는 모델의 결과를 온전히 신뢰할 수 없다. 모델이 왜 이런 결정을 내렸는지 알고, 신뢰성을 개선해야 한다.
의사 결정에 직접적 영향을 주는 것은 해석이다.
- 많은 분야에서 모델을 이용하는 이유 중 하나는 의사결정에 도움을 얻기 위해서이다.
- 따라서 의사결정권자가 납득할만한 이유를 제시해야 한다.
- 도메인 지식이 필요한 이유도 이와 유사하다.
우리가 몰랐던 지식을 얻을 기회, 편견을 깨트릴 기회가 된다.
- 맥주와 기저귀를 가깝게 진열하니 매출이 상승했다는 사례처럼, 우리가 몰랐던 지식을 알수 있다.
- 또는 예상한 결과와 정반대인 경우 고정관념을 바로잡을 기회가 되기도한다.
차원의 저주를 해결할 실마리가 된다.
- 변수 선택(Feature Selection)을 통해 중요도가 적은 변수를 제거하고, 효율적으로 인사이트를 얻을 수 있다.
1.2 모델 해석 방법의 분류
1) Intrinsic vs Post-hoc
- Intrinsic: Linear Regression, Logistic Regression과 같이 모델링 결과 parameter를 통해, 모델 그 자체로 바로 해석할 수 있는 방법
- Post-hoc: 모델링 결과를 바로 해석 할 수 없어서, 해석을 위한 새로운 모델링이나 알고리즘을 적용하는 경우
2) Model-specific vs Model-agnostic
- Model-specific: parameter 또는 그 모델의 구조로 해석하기 때문에 해석 방법이 그 모델에 특화되어 있음
- Model-agnostic: 다양한 모델에 적용할 수 있고, 모델을 학습한 후에 적용되는 해석 방법 ex) PDP, ICE, SHAP
3) Global vs Local
- Global: 전체 데이터를 아우르는 해석. 대체로 이 데이터에서 어떤 변수가 중요하고, 어떤 종류의 교호작용이 일어나는지에 대한 설명.
- Local: 각 데이터 포인트, 각 인덱스마다 해석. 이터를 더욱 문맥화하여 해석할 수 있기 때문에 전체적으로 한번에 해석하는 것보다 더욱 정확할 가능성이 높음
1.3 해석의 성질
1) fidelity
: 모델의 예측 결과와 이에 대한 해석이 얼마나 근접한지에 대한 성질
- Intrinsic 해석 방법의 경우 fidelity 매우 높음
- Post-hoc 해석 방법의 경우 fidelity가 높은지에 대한 여부는 매우 중요한 정보가 될 것
2) consistency
: 같은 데이터셋으로 학습하고, 비슷한 예측을 한 두 모델에 대하여, 각각의 해석이 얼마나 다른지에 대한 성질
- 두 모델의 예측 결과가 높은데 해석도 비슷하다면, 이 해석 방법은 매우 ‘consistent’하다
- 두 모델이 서로 예측 결과는 비슷해도 서로 다른 feature를 중심으로 학습했다면, 이러한 경우 항상 높은 consistency가 요구되는 것은 아니다.
3) stability
: 비슷한 사례 또는 인덱스에 대해, 해석이 얼마나 비슷한지에 대한 성질
- 매우 비슷한 인덱스 간 해석의 차이가 크다면, Stability가 부족. 이 경우 해석의 분산이 매우 커짐
- Consistency 성질은 서로 다른 모델간 해석이 얼마나 비슷한지에 대한 것이고, Stability는 한 모델에 대하여 비슷한 인덱스 간 해석이 얼마나 비슷한지에 대한 것
4) comprehensibility
: 해석 방법이 얼마나 인간이 이해할 수 있을 것인지
- 사람들 간 소통이 가능하고, 충분히 이해할 만한 해석은 comprehensibility가 높다
2. PDP, 부분의존도 그림(Partial Dependence Plots)
partial: 다른 변수들의 영향을 모두 고정한 상황에서, 해당 변수를 한 단위(1-unit) 증가시킬 때 변화하는 y(target)의 크기
- PDP는 특성들을 선형적으로 변환하여, 선형관계 뿐만아니라 복잡한 관계도 나타낼 수 있다.
ex) 그래디언트 부스팅 결과를 해석하려면?- 선형모델은 회귀계수를 이용하면 해석 할 수 있지만, 트리 모델은 해석할 수 없다.
- 대신 PDP를 사용하여 개별 특성과 타겟간의 관계를 볼 수 있다.
- PDP를 그릴때는 특성의 변화를 측정할 특성의 값을 grid point로 나타내는데, 이 한 점마다 예측을 진행한다.
num_grid_points=n # 샘플 x grid 포인트 만큼 예측 진행. default=10 - permutaion importance는 특성의 값을 랜덤하게 변형하고, 그떄 얼마나 에러가 커지는지를 기준으로 특성의 중요도를 산출했다. 하지만 특성이 긍정 또는 부정적으로 영향을 미치는지는 알 수 없었다. PDP로는 알 수 있다.
- PDP interaction을 사용하면 2개 특성과 타겟과의 관계를 확인할 수 있다.
구현 아이디어
1) 데이터에 등장하는 X(관심변수)의 모든 값에 하나씩, 해당 변수의 모든 샘플을 그 값으로 대체한 후 이미 학습 시킨 모델을 통해 각 샘플에 대한 예측값을 구한다. 예를들어, 성별이 관심 변수일 때 해당 변수의 모든 값을 '여성'으로 대체한 후 예측값을 구하고, 그 뒤에는 모든 값을 '남성'으로 대체한 후 예측값을 구한다.
2) 관심 변수의 각 값에 대해 구한 예측값의 평균을 낸다. 각 값에 대해 평균 예측값이 어떻게 변화하는지 plot으로 나타낸다. 즉 x축은 성별(여성, 남성)일 것이고, y축에 해당하는 값은 각각 (여성일 때 예측값의 평균, 남성일 때 예측값의 평균)임.
주의할 점
샘플 수가 굉장히 많거나 관심 변수의 Cardinality가 매우 클 경우
- 데이터가 크거나, 변수의 값이 매우 많은 연속형 변수일수록 연산량이 방대해짐
- 변수의 Parameter Space를 구성하는 원소들, 즉 해당 변수에 등장하는 값들이 정말 다양할 경우, 반복 횟수가 늘어나기 때문
- 웬만하면, cardinality가 비교적 작은 변수이거나 중요한 변수 한,두가지만 PDP를 통해 살펴보는 것이 좋을 것
변수 각 상관성이 매우 클 경우
- PDP에서는 각 변수들이 서로 상관관계가 없다고 가정
- 사실상 실제로 각 변수들 간 서로 영향이 전혀 없는 데이터는 없기 때문에 PDP 적용하기 전 유의해야 한다.
샘플 간 성질이 매우 다를 경우
- 예측값들을 평균낸 값들로 영향을 보는 것이기 때문에, 샘플들의 서로 다른 성질들이 반영되지 못한다.
- 예를 들어, 절반은 예측값이 100이고, 절반은 예측값이 -100일 때, 평균은 0이 될 것이다.
📎 Feature의 평균 영향력 및 관계 파악: PDP plot (Partial Dependence Plot)
2.1 ICE (Individual Conditional Expectation) curves
: 하나의 ICE 곡선은 하나의 특성에 대해서 타겟값의 변화를 나타낸다.
- PDP는 ICE(Individual Conditional Expectation) 곡선의 평균 곡선이다.
구현 아이디어
1) 데이터에 등장하는 X(관심변수)의 모든 값에 하나씩, 해당 변수의 모든 샘플을 그 값으로 대체한 후 이미 학습 시킨 모델을 통해 각 샘플에 대한 예측값을 구한다.
2) 구한 후 평균을 내지 않고 모든 선을 plot으로 그린다.
2.2 PDP vs ICE
ex)
Target: 회사에서 받는 bonus
X: experience(경력), degree(학위) <- 이 둘은 교호작용 존재
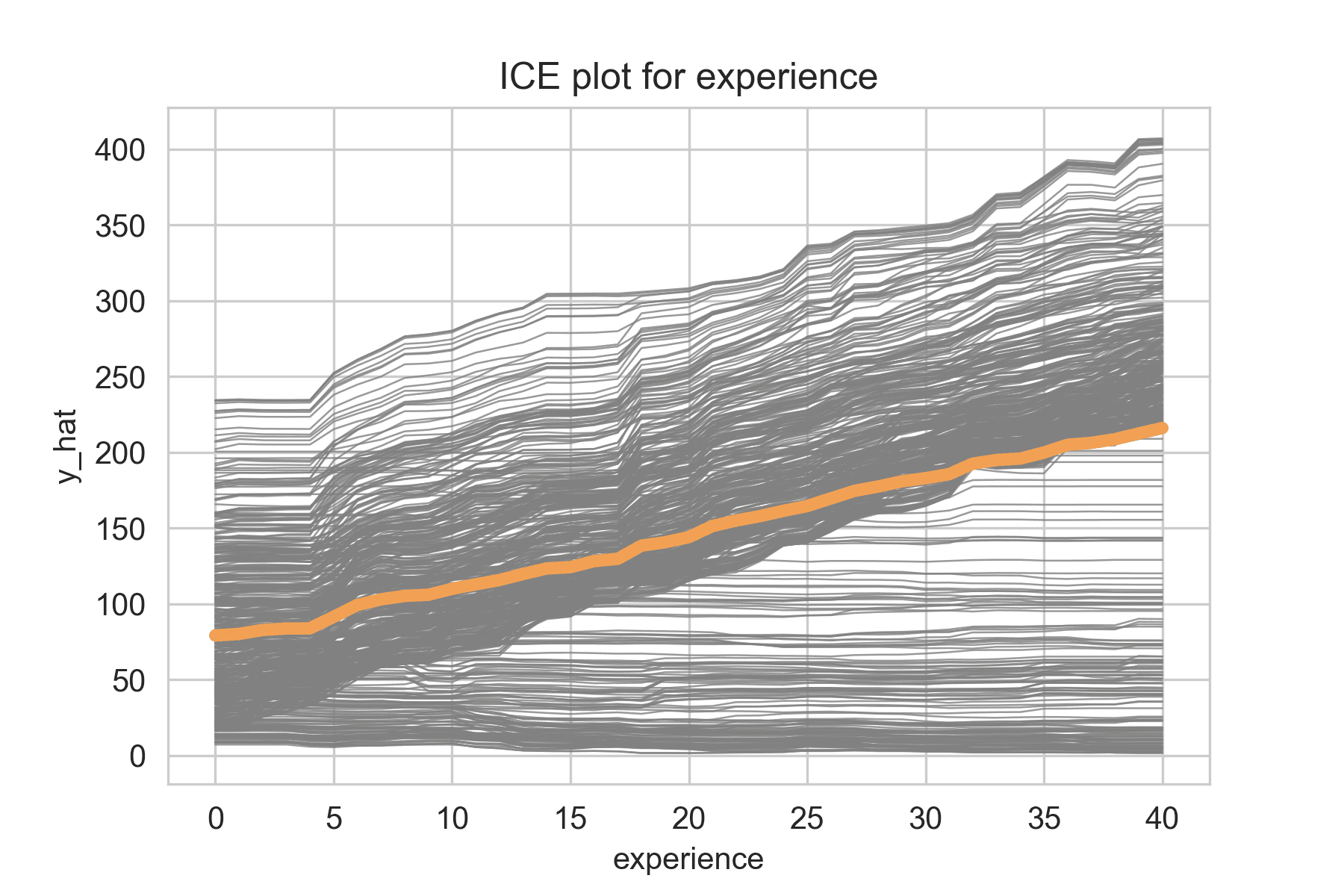
노란색 선: PDP
회색 선: ICE plot
회색선들은 똑같이 우상향하는 것이 아니라, 한 그룹은 우상향하고, 한 그룹은 평행한다.
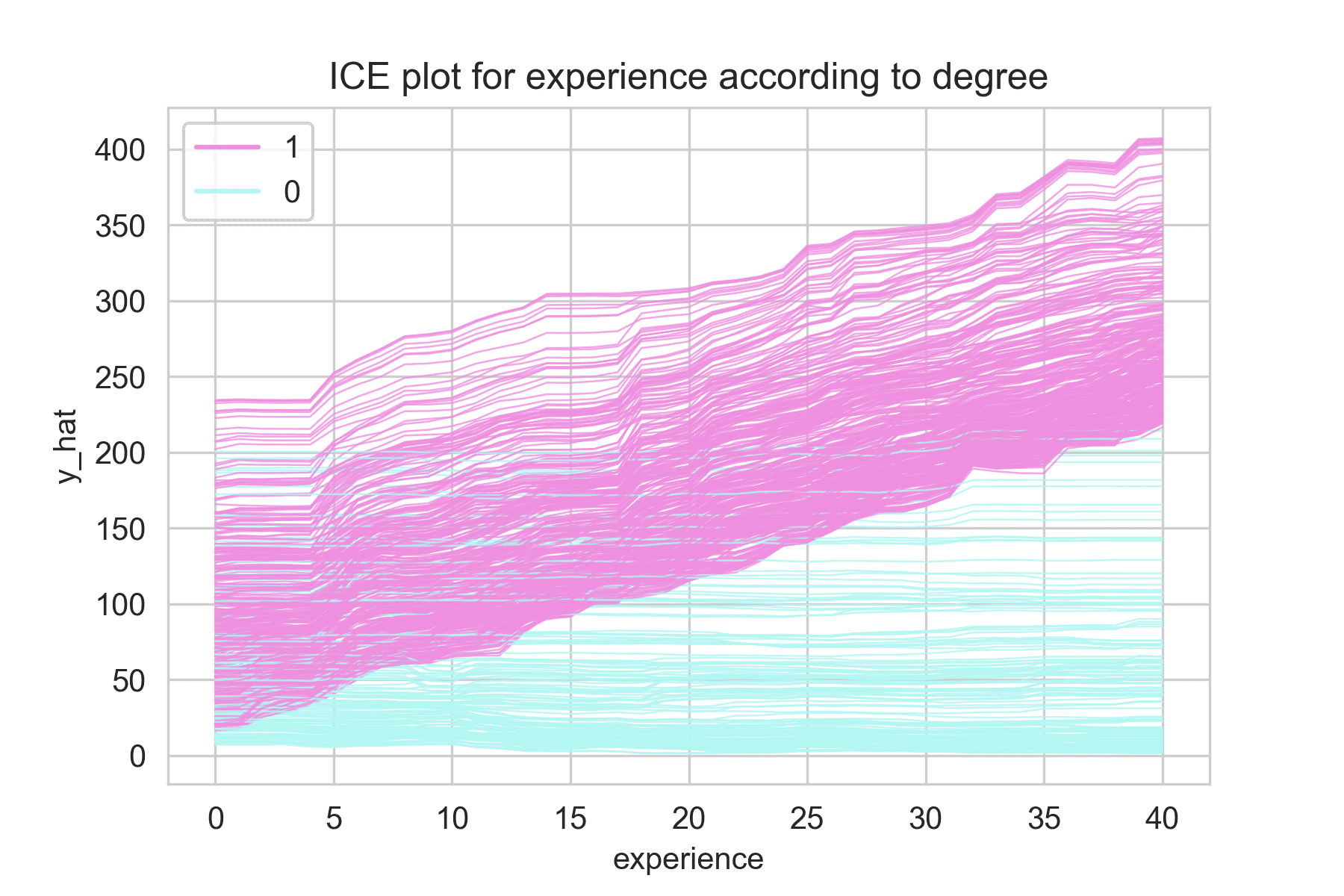
1: 학위 있음
0: 학위 없음
학위에 따라 근무경력과 보너스의 관계가 다름
학위 있으면, 근무경력 많아질 수록 보너스 증가
학위 없으면, 근무경력 상관없이 보너스 일정
-> PDP만 보면 교호작용 파악할 수 없음. ICE를 함께 그려 파악
📎 모델에 영향을 주는 교호작용 파악: ICE plot (Individual Conditional Expectation)
3. SHAP(SHapley Additive exPlanations)
: 게임이론에 나오는 이론으로써, 전체 성과에서 개인이 얼마나 공헌했는지를 수치로 나타내는 표현이다.
Shapley Values는 가능한 모든 조합을 고려한 후 한 플레이어의 평균 예상 한계 기여도를 의미한다.
아래 예를 통해 의미를 이해해보자.

-
위 예시는 앨리스와 밥이 혼자 일할 때, 앨리스가 먼저 일하고 밥이 일할때, 밥이 먼저 일하고 앨리스가 일할 때를 나타낸다.
-
게임이론에서 전략은 게임 참여자가 얻는 결과가 나 뿐 아니라 상대의 선택에 따라 달라질 때 취하는 선택을 말한다. 위 예시에서 보면 먼저 일하는 순서가 전략이라 할 수 있겠다.
-
각 상황에서 앨리스와 밥이 일한 기여도를 Marginal로 표현하고, 이러한 모든 조합을 고려한 후(Permutation), 평균을 낸것이 Shapley Value라 한다.
-
이러한 계산과정을 기반으로 하기 때문에 계산량이 굉장히 많고 샘플이 많아질수록 시간이 상당히 오래걸린다.
-
하지만 특성 간의 영향(교호작용)을 고려한 계산이 가능하고, 음의 관계도 표현할 수 있다. (개념상으로는 permutation importance 보다 정확하다.)
그외 특징)
- PDP나 특성 중요도와 달리, SHAP은 데이터 샘플 하나에 대해 설명한다.
- 즉, 관측치 하나마다 특성의 영향도가 다르게 계산될 수 있다.
3.1 SHAP Force Plot
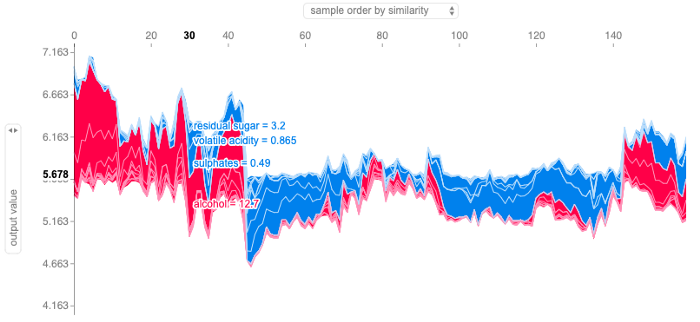
-
y 축은 타겟의 예측값을 나타낸다.
-
왼쪽 지표를 'feature X1 effects'으로 바꾸면 위쪽 지표 'feature X2'와의 타겟에 대한 영향력을 나타낸다.(PDP interaction 2개 특성과 타겟과의 관계와 유사한 기능)
-
ex. 왼쪽: lat effects 위쪽: bathrooms / bathrooms의 shap value로 나열했을 때, lat이 타겟에 미치는 영향력
-
각 point에서 feature가 양(+) 또는 음(-)의 영향을 얼마나 주는지 나타낸다.
-
특정 feature가 전체 sample에 대한 Target의 변화에 얼만큼 영향력을 발휘하는지는 알 수 없다. (SHAP Summary plot을 통해 확인)
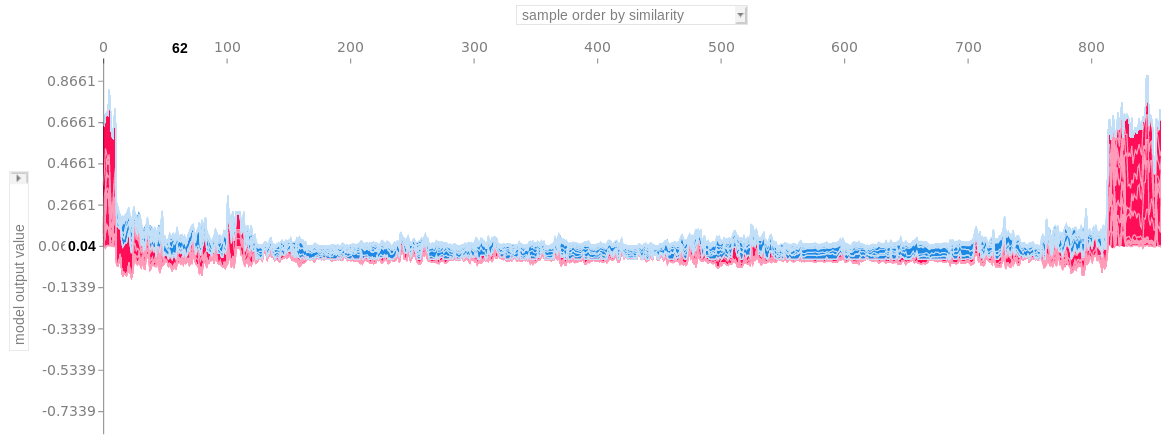
- sample order by similarity: 유사한 샘플(feature) 군집으로 정렬. 예시 이미지처럼 오른쪽 군집의 경우 암위험이 높은 군집으로 파악할 수 있다.
- sample order by output value: 모델의 예측값(target)들로 정렬. 예측값들의 순서에 따라 독립특성들이 어떤 영향을 보여주는지 파악할 수 있습니다.
- original sample ordering: 원래 샘플 순서(index)대로 정렬. 경향성 보기가 어려움.
📎 Explain Any Models with the SHAP Values — Use the KernelExplainer
3.2 SHAP Summary Plot
Scatter
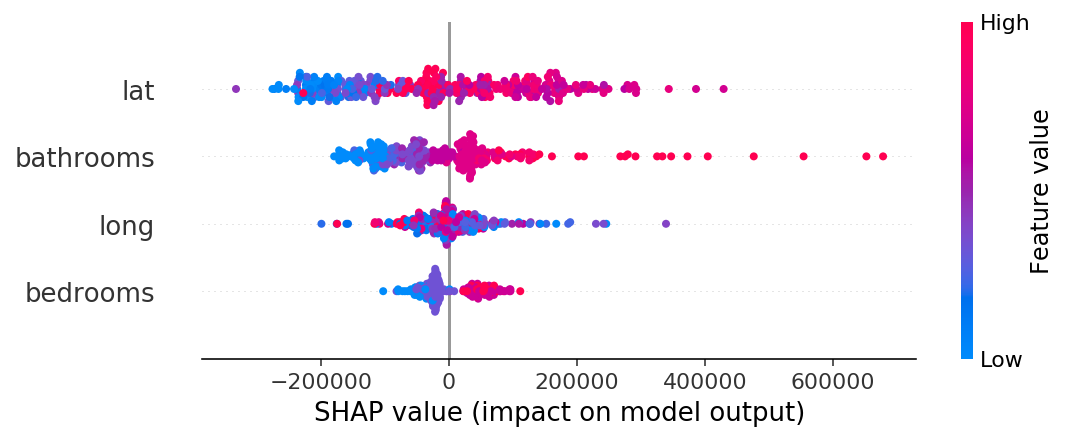
- feature들이 타겟에 주는 영향력을 요약하였다.
- x축 SHAP value는 피처가 target에 주는 영향을 나타낸다.
- 위 그림은 집값(target)예측 모델로써, lat(위도) 점들이 0이하에 주로 몰려 있어 집값을 낮추는 영향을 주었다.
- Feature value는 피처의 자체의 값을 색으로 표현한다. 스케일링 된 값이라 생각하면 편하다.
- 빨간색 lat은 고위도, 파란색 lat은 저위도를 나타낸다.
Violin
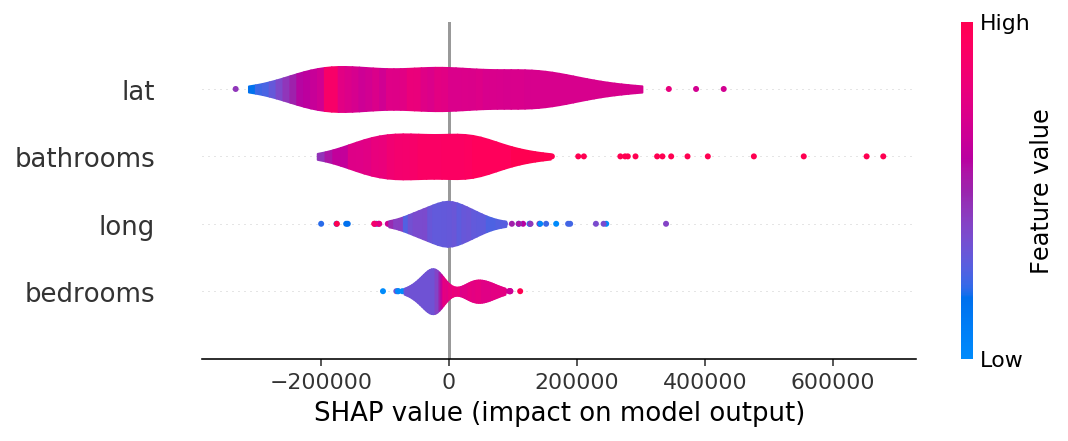
- 같은 결과를 violin plot으로 나타내보자
- lat은 분산이 크며, 음과 양으로 영향을 많이 주고 있다.
- bedroooms은 크게 영향을 미치지 못하고 있다.
- 점으로 나타나는 부분은 이상치를 나타낸다.
Bar
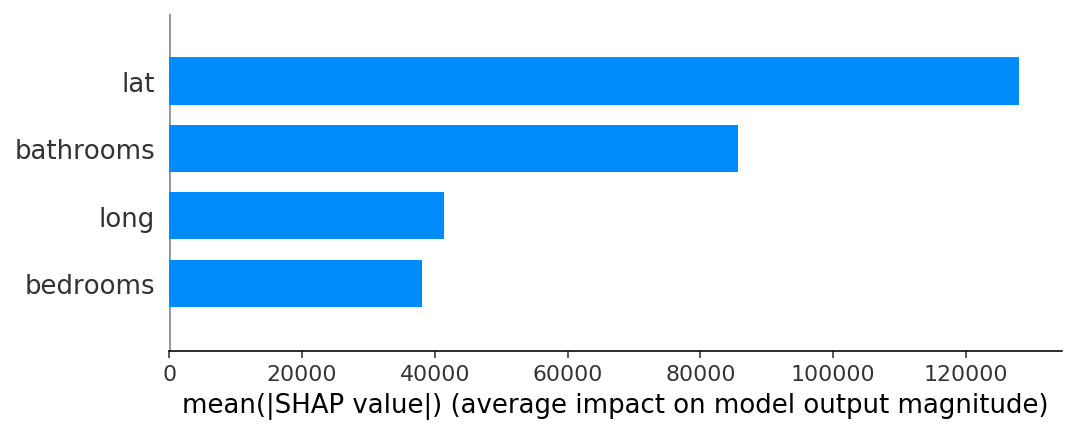
- SHAP value를 절댓값 씌우고 평균낸 값으로써, feature importance와 비슷한 역할을 한다.
정리
서로 관련이 있는 모든 특성들에 대한 전역적인(Global) 설명
- Feature Importances
- Drop-Column Importances
- Permutaton Importances
타겟과 관련이 있는 개별 특성들에 대한 전역적인 설명 (전체 관측치에 대해)
- Partial Dependence plots
개별 관측치에 대한 지역적인(local) 설명 (개별 관측치에 대해)
- Shapley Values
이러한 방법을 사용하여 모델의 설명력을 높일 수 있다. 물론, 이러한 설명이 신뢰를 주려면 모델 성능이 좋아야 한다.
