11. 행렬 거듭제곱

준 사망 상태에 이르렀던 알고리즘 공부... 물론 문제는 매일매일 풀었지만, 단순 풀이에 그치지 않고 개념을 정리하고 내 것으로 체득하는 과정을 정리하는 것은 너무 오랜만인 것 같다.

개인적으로 알고리즘 문제 유형 중에서 DP를 가장 어렵게 생각하고 있다. 웬만한 DP 문제는 우선 단위마다 문제를 분할하는 것이 우선인데, 그 분할의 과정 속에서 직접 그려보거나 적지 않으면 알아채기 힘든 수식이 숨겨져 있고 나는 그런 부분에서 많이 약점을 노출한다. 그리디도 그런 이유로 적용을 힘겨워하는 편이다.

얼마 전, 똑같은 제목(즉, 시리즈 문제)의 두 문제를 풀었는데 같은 문제임에도 주어진 환경(시간 제한, 메모리)에 따라 풀이를 취사선택해야 하는 케이스를 마주했다. 앞의 문제는 익히 풀어온 DP 유형이어서 쉽게 풀었지만, 뒤의 문제는 더 극악의 환경 내에서 문제 풀이를 수행해야 해서 기존의 DP로는 풀이할 수 없는 문제였고 여기서 행렬 연산과 고속 거듭제곱을 같이 활용하는 연습을 진행할 수 있었다.

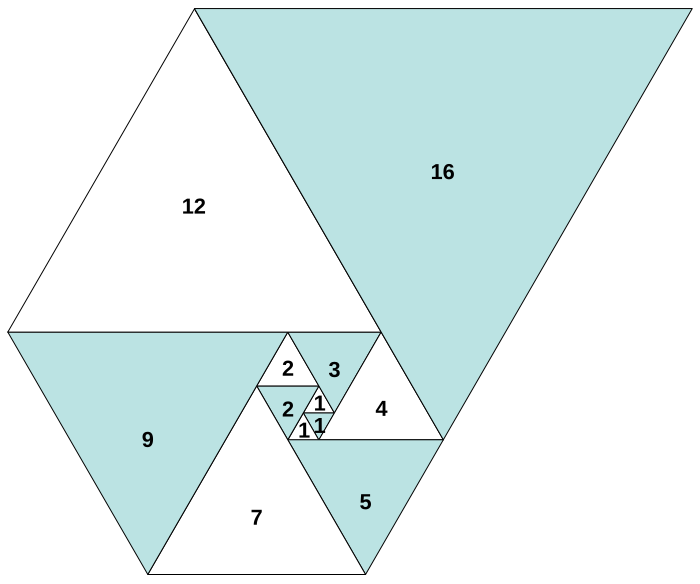
위의 그림은 파도반 수열(Padovan Sequence)이라고 한다. 정삼각형을 안쪽에서 바깥쪽으로 나선을 그리듯 길이에 맞춰 늘이며 붙여나가면서 산출되는 한 변의 길이들을 일련화한 수열($P(N)$)이며, 관련하여 주어지는 문제는 $N$이 주어질 때, $P(N)$을 구하는 것이다.

1) 파도반 수열 1

$N$의 범위, 시간 제한과 메모리는 아래와 같다.

• 범위 : $1 ≤ N ≤ 100$
• 시간 제한 : 1s
• 메모리 : 128 MB

$N$의 범위가 작은 편이어서 DP 풀이로도 충분히 풀어낼 수 있으며, 점화식만 찾아내면 쉽게 재귀함수로 풀이를 유도해낼 수 있다.

수열은 아래와 같다.

$1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16...$

위의 그림에서 임의의 한 정삼각형($P(N)$)을 두고, 해당 정삼각형의 한 변의 길이를 지닐 수 있는 평행사변형의 한 변을 찾는 방식으로 점화식을 유도한다. 그렇게 하면 아래와 같은 두 개의 점화식이 나온다.

$P(N) = P(N-1) + P(N-5) ⋯ (a)$

$P(N) = P(N-2) + P(N-3) ⋯ (b)$

둘 다 똑같이 파도반 수열을 나타내는 점화식이긴 하지만, 나는 (b) 점화식을 선택해서 풀이하였다. 세 개 이상의 항이 나오는 점화식은 그 간극이 짧을 수록 풀이 과정에서의 변수를 통제하기 용이하겠다는 나름의 판단 때문이었다.

풀이 링크는 아래와 같다.

https://github.com/kimD0ngjun/backjoon_programmers/blob/main/%EB%B0%B1%EC%A4%80/Silver/9461.%E2%80%85%ED%8C%8C%EB%8F%84%EB%B0%98%E2%80%85%EC%88%98%EC%97%B4/%ED%8C%8C%EB%8F%84%EB%B0%98%E2%80%85%EC%88%98%EC%97%B4.py

2) 파도반 수열 2

동일한 문제지만, $N$의 범위, 시간 제한과 메모리는 전술한 문제와 다르다.

• 범위 : $1 ≤ N ≤ 10^{18}$
• 시간 제한 : 1s
• 메모리 : 1024 MB

메모리가 8배 늘어났지만, $N$의 범위가 자바로 치환하면 int 범위를 넘어서 long 범위가 된다. 즉, 기존의 메모이제이션으로는 풀이할 수 없다는 것이다.

(1) 기존 풀이의 단점

메모이제이션, 즉 DP의 최대 단점은 문제 최적화를 수행해서 시간 소모를 줄였다고 한들 결국 그만큼 공간을 차지하게 된다. 중복 계산을 피하기 위해 이전에 수행한 계산의 답을 저장하는 데에는 메모리가 쓰이기 때문이다.

또한, 시간 소모를 줄이는 것은 절대적인 것이 아니라 비례적으로 줄어들게 된다. 무슨 말인고 하니, 중복 계산이라는 것은 이전에 했던 계산을 한번 더 하는 것이지 불필요한 계산을 한번 하는 것은 중복 계산이 아니기 때문에 로직상 수행이 전제된다.

일반적인 메모이제이션의 시간 복잡도는 $O(n)$ 내지는 $O(n^3)$ 정도로 나온다. 이것은 중첩된 반복문의 전체 탐색과 비슷한 정도이기 때문에 메모이제이션은 최적화에 특화됐지, 그 이상의 효과를 기대하기는 힘들다.

(2) 불필요한 계산 없애기

예를 들어서, $2^4$를 컴퓨터의 시점으로 계산한다고 가정하자.
보편적으로 우리는 저것의 값을 계산할 때, 2를 4번 거듭제곱하는 것임을 알고 있다. 그것을 사고 과정으로써 표현하자면...

1. 2를 제곱하면 4가 나온다. 이때, 지수는 2다.
2. 이 4를 한번 더 제곱하면 16이 나온다. 이때, 지수는 16이다.
3. 그렇기 때문에 2의 4제곱은 16이다.

이걸 단순 수식으로 표현해서(즉, 알고리즘을 지정하지 않고) 컴퓨터에게 넘긴다면, 컴퓨터는 저 계산 중간에 하나를 더 추가한다.

1. 2를 제곱하면 4가 나온다. 이때, 지수는 2다.
2. 4에 2를 한 번 더 곱하면 8이 나온다. 이때, 지수는 3이다.
3. 이 8에 2를 한 번 더 곱하면 16이 나온다. 이때, 지수는 16이다.
4. 그렇기 때문에 2의 4제곱은 16이다.

보면 계산 과정이 한 번 더 추가됐으며, 저 과정을 불필요한 계산이라고 칭할 수 있겠다. 즉 반복해서 곱한다는 것을 의미한다. 지금이야 $2^4$이라는 아주 작은 숫자여서 계산이 딱 한 번 추가됐지, 지수의 범위가 상당히 커지게 되면 저 불필요한 계산이 여러 번 나오면서 시간 소모 및 메모리 낭비가 극심해질 것이다.

앞서, 밀러-라빈 소수 판별 테스트를 공부할 때 익혔던 고속 거듭제곱 알고리즘이 이런 반복되는 불필요한 계산 포함 산출을 효율적으로 다듬는 분할 정복 알고리즘의 훌륭한 예시라고 할 수 있다.

# a의 b제곱을 구하기
def power(a, b):

    result = 1

    while b > 0:
        # b가 홀수일 경우
        if b % 2 != 0:
            # result에 밑 한 번 더 곱하기
            result = result * a

        # 제곱한 만큼 b는 2로 나눠주고
        # 홀수, 짝수 상관없이 a는 제곱
        b = b // 2
        a = a * a

    return result

위의 고속 거듭제곱 알고리즘의 시간복잡도는 $logN$이 나온다.

다만, 단순 수식(정확한 표현으로는 공비가 일정한 등비수열)일 경우에는 문제가 없지만 위의 파도반 수열처럼 규칙성이 점화식으로써 표현되는 경우는 일반적인 고속 거듭제곱 알고리즘을 차용하기가 난감하다. 그렇기 때문에 추가적으로 접목할 내용이 행렬이다.

(3) 점화식과 행렬

앞서 첫 번째 문제에서 찾았던 점화식을 다시 한 번 더 정리하자면 아래와 같다.

$P(N) = P(N-2) + P(N-3)$

점화식은 일반화를 하기 위한 단서일 뿐이지 점화식 자체로 수열을 일반화할 수는 없다. 즉, 점화식을 추가로 유도해서 일반화할 수 있는 수식을 찾아야 한다.

위의 점화식에서 $N$의 범위는 $N > 3$이다. 그래서 우선 시작 포인트로 삼을 항들을 정리해보면 아래와 같다.

$P(1) = 1$

$P(2) = 1$

$P(3) = 1$

주어진 항들이 총 세 개이기 때문에, 주어진 점화식까지 포함해서 추가 점화식이 최소 3개가 필요해진다. 유도 과정을 거쳐본다.

$P(N) = P(N-2) + P(N-3)$

$P(N+1) = P(N-1) + P(N-2)$

$P(N-1) = P(N-1)$

이를 통해 유도할 수 있는 거듭제곱 단위가 되는 행렬을 포함한 최종 점화식 및 수열 일반화 결과는 아래와 같다.

$\begin{pmatrix}0&1&1\\1&0&0\\0&1&0 \end{pmatrix}$$\begin{pmatrix}P(N)\\P(N-1)\\P(N-2) \end{pmatrix}$ = $\begin{pmatrix}P(N+1)\\P(N)\\P(N-1) \end{pmatrix}$

$\begin{pmatrix}0&1&1\\1&0&0\\0&1&0 \end{pmatrix}^{N-2}$$\begin{pmatrix}P(3)\\P(2)\\P(1) \end{pmatrix}$ = $\begin{pmatrix}P(N+1)\\P(N)\\P(N-1) \end{pmatrix}$

아니 라텍스 문법 행렬 중앙정렬 어케함

이 점화식 및 일반식을 고속 거듭제곱에 차용하되, 행렬 연산 함수를 추가로 작성해서 적용하면 풀이를 수행할 수 있다.

풀이 링크는 아래와 같다.

https://github.com/kimD0ngjun/backjoon_programmers/blob/main/%EB%B0%B1%EC%A4%80/Gold/27435.%E2%80%85%ED%8C%8C%EB%8F%84%EB%B0%98%E2%80%85%EC%88%98%EC%97%B4%E2%80%852/%ED%8C%8C%EB%8F%84%EB%B0%98%E2%80%85%EC%88%98%EC%97%B4%E2%80%852.py