문제 해설

import java.io.*;

public class Main {

    static int countZero, countOne;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int T = Integer.parseInt(br.readLine());

        while (T-- > 0) {
            int N = Integer.parseInt(br.readLine());
            countZero = 0;
            countOne = 0;
            fibonacci(N);
            System.out.println(countZero + " " + countOne);

        }
    }

    private static int fibonacci(int n) {
        if (n == 0) {
            countZero++; // 0 출력 횟수
            return 0;
        } else if (n == 1) {
            countOne++; // 1 출력 횟수
            return 1;
        } else {
            return fibonacci(n - 1) + fibonacci(n - 2);
        }
    }
}

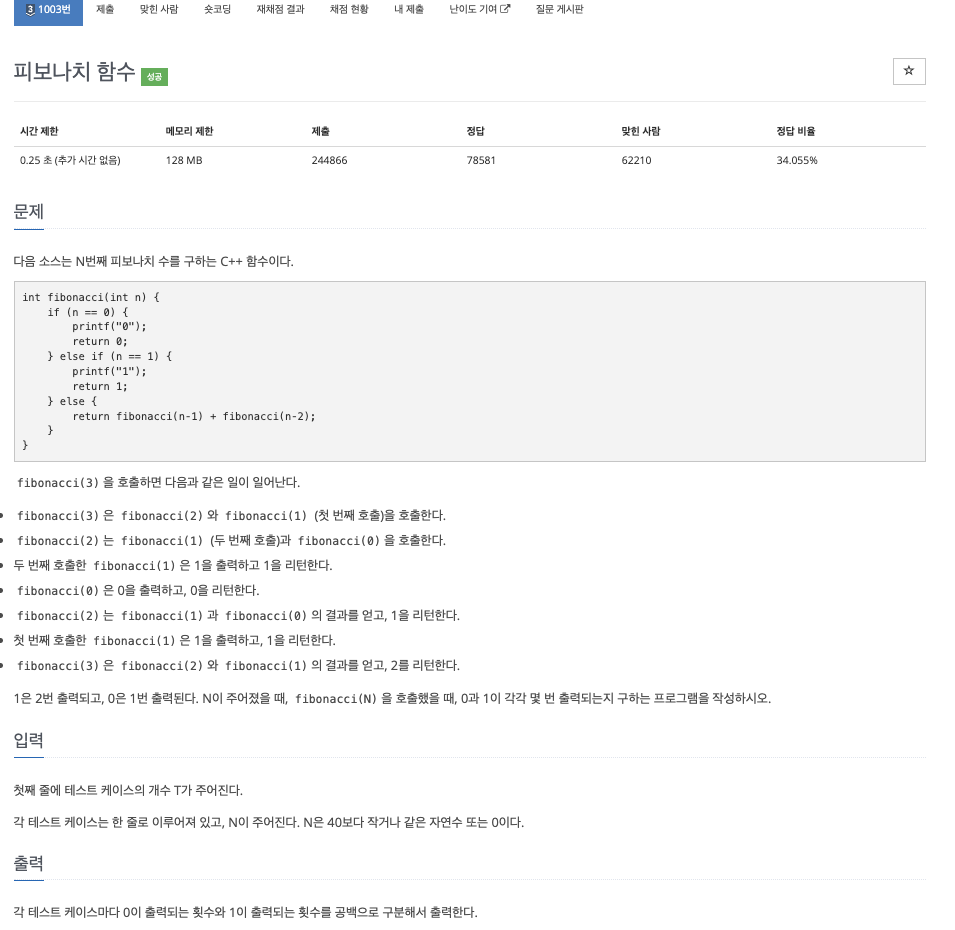
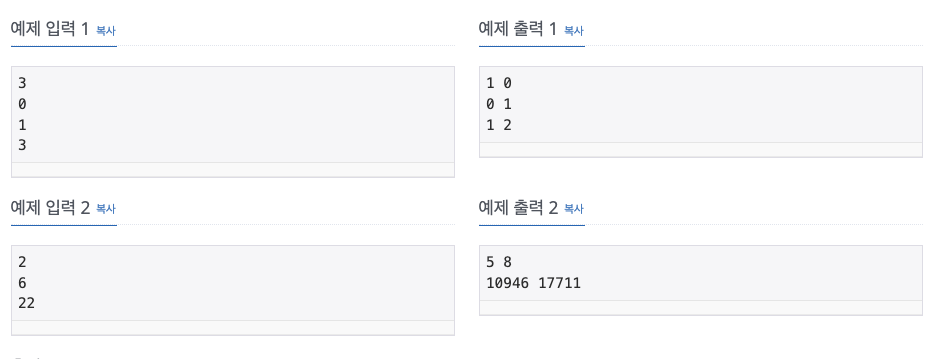
이런 식으로 기존의 피보나치 코드에다가 출력 횟수만 추가하면 중복된 계산량이 많아 시간 초과가 발생한다. 계산이 중복되는 것을 방지하기 위해 DP를 사용하여 이미 한 번 연산했던 값은 재사용해야하는 문제이다.

문제 해설

이번 문제는 피보나치 수에서 0과 1이 호출되는 횟수를 구하는 것이다. 처음에 N이 입력되면 N - 1, N - 2, ... 0까지 N 이하의 모든 수들이 결국 0과 1을 찾기 위하여 자신들보다 작은 수를 재귀호출할 것이다.
때문에 N에 관한 정답이 구해진다면 이후에 N 이하의 수가 입력된다면 다시 계산할 것 없이 이미 한 번 연산되어 DP 테이블에 저장되어 있는 dp[N] 값을 바로 꺼내와 반환하면 되므로 계산 과정을 획기적으로 단축시킬 수 있다.

Java 정답 코드

import java.io.*;

public class Main {

    static Integer[][] dp = new Integer[41][2]; // 인덱스 n : [0 출력 횟수, 1 출력 횟수]

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int T = Integer.parseInt(br.readLine());

        dp[0][0] = 1; // N = 0일 때, 0 호출 횟수
        dp[0][1] = 0; // N = 0일 때, 1 호출 횟수
        dp[1][0] = 0; // N = 1일 때, 0 호출 횟수
        dp[1][1] = 1; // N = 1일 때, 1 호출 횟수

        while (T-- > 0) {
            int N = Integer.parseInt(br.readLine());
            fibonacci(N);
            bw.write(dp[N][0] + " " + dp[N][1] + "\n");
        }

        bw.flush();
        bw.close();
    }

   private static Integer[] fibonacci(int N) {
      // 만약 N에 대한 0과 1의 호출 횟수가 아직 계산되지 않았다면 계산 수행
      if (dp[N][0] == null || dp[N][1] == null) {
          // N번째 피보나치 수에서 0이 출력되는 횟수는
          // (N-1번째 피보나치 수에서 0이 출력되는 횟수) + (N-2번째 피보나치 수에서 0이 출력되는 횟수)
          dp[N][0] = fibonacci(N - 1)[0] + fibonacci(N - 2)[0]; 

          // N번째 피보나치 수에서 1이 출력되는 횟수는
          // (N-1번째 피보나치 수에서 1이 출력되는 횟수) + (N-2번째 피보나치 수에서 1이 출력되는 횟수)
          dp[N][1] = fibonacci(N - 1)[1] + fibonacci(N - 2)[1];
      }

      // N번째 피보나치 수에서 0과 1이 출력된 횟수를 담은 배열 반환
      return dp[N];
  }

Python 정답 코드

import sys

sys.setrecursionlimit(10**6)
input = sys.stdin.readline

T = int(input())

dp = [[None, None] for _ in range(41)]

dp[0][0] = 1
dp[0][1] = 0
dp[1][0] = 0
dp[1][1] = 1


def fibonacci(N):
    if dp[N][0] is None or dp[N][1] is None:
        dp[N][0] = fibonacci(N - 1)[0] + fibonacci(N - 2)[0]
        dp[N][1] = fibonacci(N - 1)[1] + fibonacci(N - 2)[1]

    return dp[N]


for _ in range(T):
    N = int(input())
    print(fibonacci(N)[0], fibonacci(N)[1])