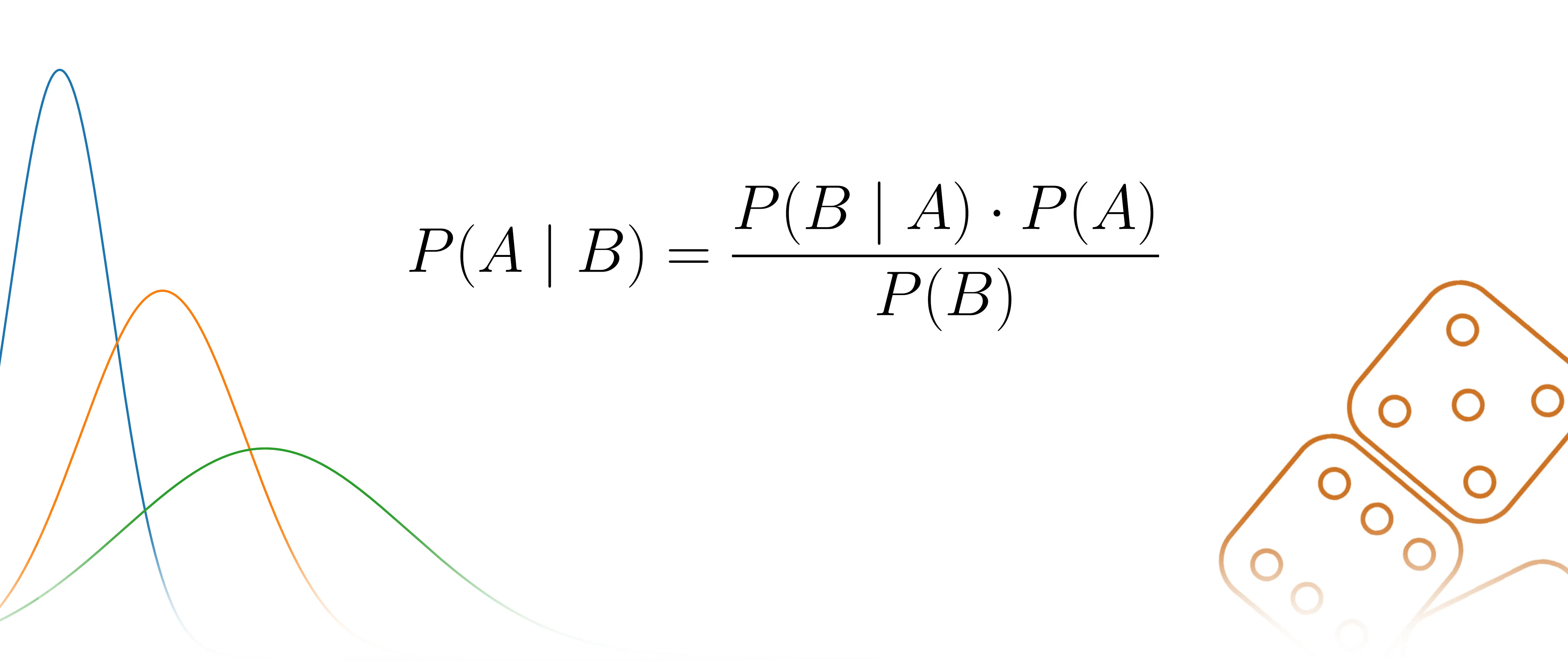What is Bayesian inference

Bayesian inference는 목표로 하는 "특정한 분포"를 inference(추론)하는 방법중의 하나이다. 이 포스팅에서는 목표로 하는 특정 분포를, Data를 생성하는 분포로 생각하고 정리하는 것이 Bayesian inference를 이해하는데 도움이 될 것이다.

Prior Distribution

Bayesian inference를 알아보기 전에, 다음 내용을 가정해야 한다.

"세상의 Data는 이를 생성해내는 분포에서 Sampling된 것이고, 이 분포는 Parametric 분포이다."
사실 위 가정이 하늘에서 뚝, 떨어진것은 아니다. 이는 Manifold hypothesis를 참고하면 좋을 것 같다.

위 가정에 의해, 우리가 Data생성 분포의 Parameter를 잘 찾는다면, Data를 생성하는 분포를 찾을 수 있고, 그 분포에서 Sampling하는 과정을 통해 실제 Data를 생성할 수 있게 된다.

그렇다면, 그 Parameter는 어떻게 생성되는가? 라는 질문에 도달하게 된다. Bayesian inference에서는 위에서와 동일한 방법을 사용한다. 즉, 이 Parameter 또한 특정한 분포에 의해서 발생된다는 것이다. 우리는 이 Parameter를 생성하는 분포를 Prior Distribution, 줄여서 Prior이라고 칭하고, $P(H)$으로 표기한다.
여기서 $H$는 hypothesis(가설)으로 표현했을 뿐이지, 우리의 Parameter, model의 weight, w 쯤으로 생각하면 된다.

사실 이러한 접근법이 혼란스러운건 사실이다. 결론적으로 말하면, 우리는 많은 경우에 Prior를 관측(Observe)할 수 없다(어렵다). 하지만, Prior을 정의하므로써, 우리가 선택한 Parameter가 생성될 확률을 표현할 수 있고, 이러한 표현으로 수학적 해석에 용이하기 때문에 정의했다고 생각하자.

Likelihood

그렇다면, 우리가 Data를 생성하는 분포를 추정하기 위해 사용할 수 있는 정보는 무엇인가? 당연하게도 Data이다. 우리는 이미 특정한 Data를 가지고 있고, 이 Data가 생성되는 분포를 추정하고 싶은 것이니 말이다. 위에서 언급했던 것처럼, 이 Data는 Parametric 분포에서 생성되고, 이를 적극적으로 활용하기 위해 $P(E|H)$로 표현할 수 있다. 여기서 $P(E|H)$는 Likelihood로 부르고, $E$는 Evidence(증거), Data쯤으로 생각하면 된다. 또한, $P(E|H)$의 의미를 생각해 보면, 우리가 특정한 $H$를 골랐을 때, 이 $H$의 영향을 받아 Data가 생성되었을 확률을 의미한다.

Posterior Distribution

정리하자면, 우리는 Data를 생성하는 분포를 추론하고 싶고, 궁극적으로는, 이 Data를 생성하는 분포의 Parameter를 찾고 싶은것이다. 이를 수식으로 표현하자면 $P(H|E)$으로 표현 할 수 있고, Posterior Distribution, 줄여서 Posterior으로 부른다. Posterior의 의미를 생각해보면, 주어진 Data가 있을 때, 우리의 Parameter($H$)가 발생할(맞을)확률 정도로 생각할 수 있다.

Bayes' Rule

위에서 Priror, Likelihood, Posterior의 의미와 수식을 정립했는데, 이들간의 관계에 대해서 생각해 보면 Bayes' Rule에 의해 다음과 같다

여기서 $P(E)$는 우리가 가지고 있는 Data($E$)가 변함이 없다면 상수로 고정될 것이고, 다음과 같은 특징을 찾을 수 있다.

Bayesian inference

마지막으로, 위의 내용을 모두 정리하면 다음과 같다.
우리가 가지고 있는 Data를 생성하는 분포를 구성하는 Parameter를 찾으려고 한다. 그렇다면, 다양한 Parameter중, 어떤 Parameter가 정답과 가장 유사할까?
의미적으로는, Posterior이 최대확률을 가지는 Parameter가 가장 유사할 것이다. 이러한 방법을 Maximum A Posterior(MAP)이라고 한다. 하지만, Posterior을 구하기 어려운 상황에서는 대안이 없을까? Bayes' Rule에서 결론낸 것 처럼, Posterior은 Prior과 비례하기 때문에, Likelhood의 최대 확률을 가지는 Parameter또한 좋은 Parameter가 될 수 있다. 이러한 방법을 Maximum Likelihood Estimation(MLE)라고 부른다. 다만, 두 관계에 의해 일반적으로는 MAP이 MLE보다 더 정확한 지표임을 확인할 수 있다.

결론적으로, Bayesian inference는 위에서 나열한 가정을 통해 목적하는 분포를 추정하는 것인데, 이 포스팅의 독자들은 이 포스팅에서 설명한 순서의 역순으로 개념을 확인해 보는 것이 좋을 것 같다. Priror, Likelihood, Posterior이 하늘에서 뚝, 하고 떨어진 것이 아니고, Bayes' Rule에 의해 당연하게 생각해 볼 수 있는 과정이었음을 확인해 보시길 바란다.