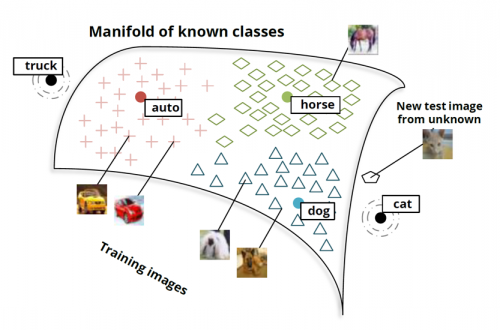
What is Manifold hypothesis?

출처 : Wikipedia, 블로그

Manifold hypothesis는 Generative Model을 비롯한, 다양한 기계학습 모델의 기저에서 사용되는 가설이다.
Wikipedia의 원문을 빌려 설명하자면 다음과 같다.

The manifold hypothesis posits that many high-dimensional data sets that
occur in the real world actually lie along low-dimensional latent manifolds
inside that high-dimensional space.

즉, 실제로 세상에서 얻어지는 고차원 data들은, 고차원 공간 내부의 저차원의 "latent manifold"로 존재한다는 가설이다.
그러므로, 우리가 그 실제 data와 latent사이의 mapping 함수를 안다면, 고차원인 실제 데이터를 저차원으로 표현할 수 있는 방법을 찾게 되는 것이다. 이러한 함수와 그 역함수에 대해서 알게 된다면, 다음 두가지 생각을 할 수 있다.

고차원 $\rightarrow$ 저차원 으로의 mapping:

• 더 적은 차원으로 정보를 표현할 수 있으므로, "정보의 압축"이라는 관점에서 중요하다.
• 더 적은 차원에서 데이터를 비교할 수 있으므로, "데이터 분석"적으로 난이도를 낮추는 것이다.

---

실제로, 많은 Generative model들의 방법은, data를 통해 latent를 추론하고 해당 latent로부터 데이터를 생성하도록 설계 되었다.

VAE(Variational autoencoder)의 경우, 특정 latent의 분포를 Gaussian으로 특정하고, model의 output을 Gaussian의 parameter인 $\mu$(평균)와 $\sigma$(분산)으로 설정한다.
여기서, model의 입력값인 $x$의 categorical 한 정보를 $\mu$, $\sigma$ 로 표현하고, 이 Gaussian의 한 point인, latent가 $x$의 저차원 정보라고 생각해 보자.
이렇게 설계된 latent를 실제 data로 mapping하는 함수를 찾는다면 우리는 다음 두 함수를 찾는것과 같다.

• $q_{\phi}():$고차원 $\rightarrow$ 저차원
• $p_{\theta}():$고차원 $\rightarrow$ 저차원

이 밖에도, GAN을 포함한 다양한 generative model들이 Manifold hypothesis에 기반을 두고있다.