정수 삼각형

문제 설명

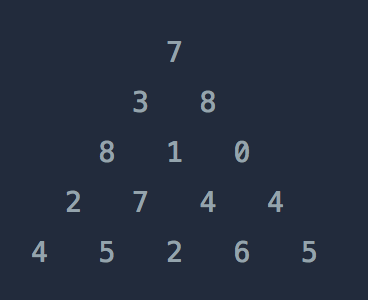
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.

삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.

해결한 로직

class Solution {
    public int solution(int[][] triangle) {
        int answer = 0;
        int stage = triangle.length-2;
        int index = 0;
        for(int i=stage; i>-1; i--)
            for(int j = 0; j<triangle[i].length; j++){
                if(triangle[i+1][j]>=triangle[i+1][j+1])
                    triangle[i][j] += triangle[i+1][j];
                else
                    triangle[i][j] += triangle[i+1][j+1];
            }
                return triangle[0][0];
    }
}

• 처음에는 방향이 잡히지 않아 모든 경우의 수를 고려하는 로직을 구현하려고 하였는데,
  재귀함수를 짜면서 이건 잘못된 길이 분명함을 깨달았다.
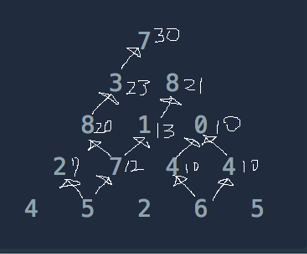
  (최악의 경우 2^500개의 경우의 수가 나온다)
  
  
• 그래서 어떻게 해야할까 고민하다가 삼각형의 밑에서 부터 경우의 수를 줄이며 올라가는 방식을 생각해냈다.
  
• 해결을 하고 찾아보니 문제 해결법 중, Bottom-up 방식이 바로 이러한 방식이라고 한다.

Bottom-up 방식

• 우리말로 상향식이라고도 한다. 가장 작은 문제들부터 답을 찾아 가면서 마지막에는 전체 문제의 답을 구하는 방식이다.
• 보통 반복문을 이용해 구현하게 된다. 재귀 호출을 하지 않으므로 시간과 메모리의 사용량이 상대적으로 적다는 이점이 있다.
  

오늘의 회고

오늘은 심화프로젝트 설계와 알고리즘 문제(정수 삼각형)를 풀었다
풀다가 정말 기발한 아이디어라고 생각해서 신났는데,
찾아봤더니 유명한 알고리즘 문제풀이법 중 하나라고 해서 조금 실망했다.
그래도 2^500가지의 경우의 수를 보지않는 효율적인 로직을 생각해내서 뿌듯하다.