MST란

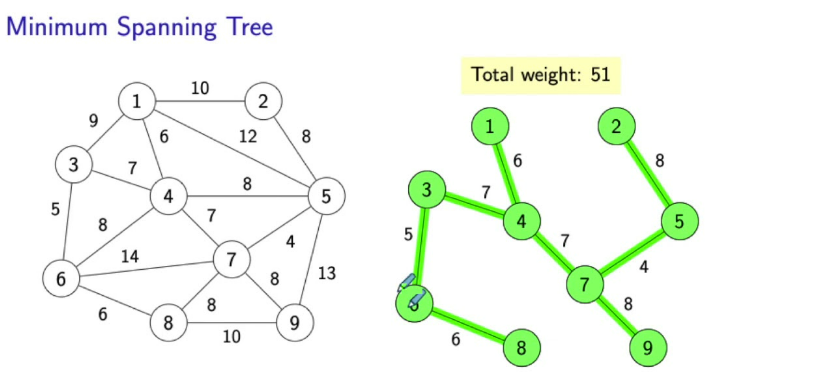
Minimum Spanning Tree(MST)는 최소 스패닝 트리로 하나의 시작점에서 다른 모든 노드까지의 최단 경로를 찾는 것이 목표이다.

즉 그래프의 모든 노드를 포함하는 최소 비용 트리를 반환한다. 모든 노드를 방문해야 하며, 경로는 중요하지 않고 총 비용이 최소가 되는 트리를 만듭니다.

Dijkstra와의 차이

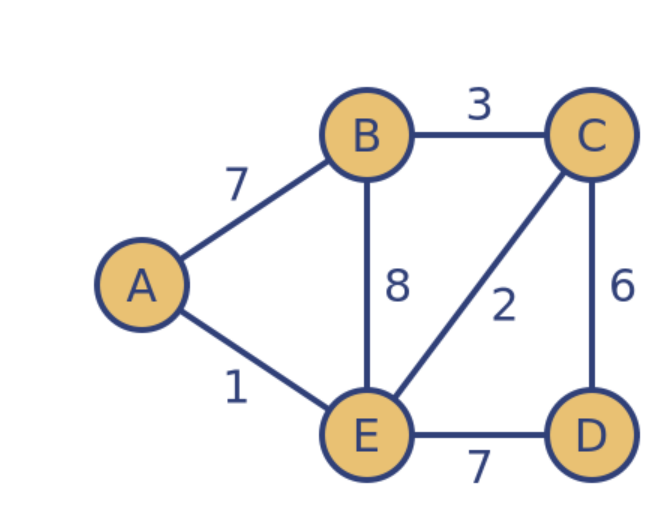
Dijkstra는 한 노드에서 각기 다른 노드들까지 도착할 수 있는 최소 값을 구하는 것으로 모든 노드들이 연결돼있을때 최소 값을 구하는 MST와는 차이가 있다.

Dijkstra에서 c까지는 3이겠지만 MST에서는 굳이 A에서 연결한 값을 더할 필요가 없기때문에 E에서 바로 C로 가는 2가 나온다.

MST 예시 문제

백준 1197 최소 스패닝 트리

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;

int v, e;
int mst[10001];
vector < pair<int, pair<int, int>>> li;
int result = 0;

//-2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.

int find(int x) {
	if (mst[x] == x) return x;
	return mst[x] = find(mst[x]);
}	

void _union(int x, int y) {
	x = find(x);
	y = find(y);
	if (x > y) {
		mst[x] = y;
	}
	else {
		mst[y] = x;
	}
}

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	cin >> v >> e;

	//초기화
	for (int i = 0; i <= v; i++) {
		mst[i] = i;
	}

	for (int i = 0; i < e; i++) {
		int a, b, c;
		cin >> a >> b >> c;
		li.push_back({ c,{a,b} });
	}

	sort(li.begin(), li.end());

	for (int i = 0; i < li.size(); i++) {
		int x = li[i].second.first;
		int y = li[i].second.second;
		//부모가 같이 않으면 사이클이 발생할 수 없음
		if (find(x) != find(y)) {
			//연결함
			_union(x, y);
			result += li[i].first;
		}
	}

	cout << result;

	return 0;
}