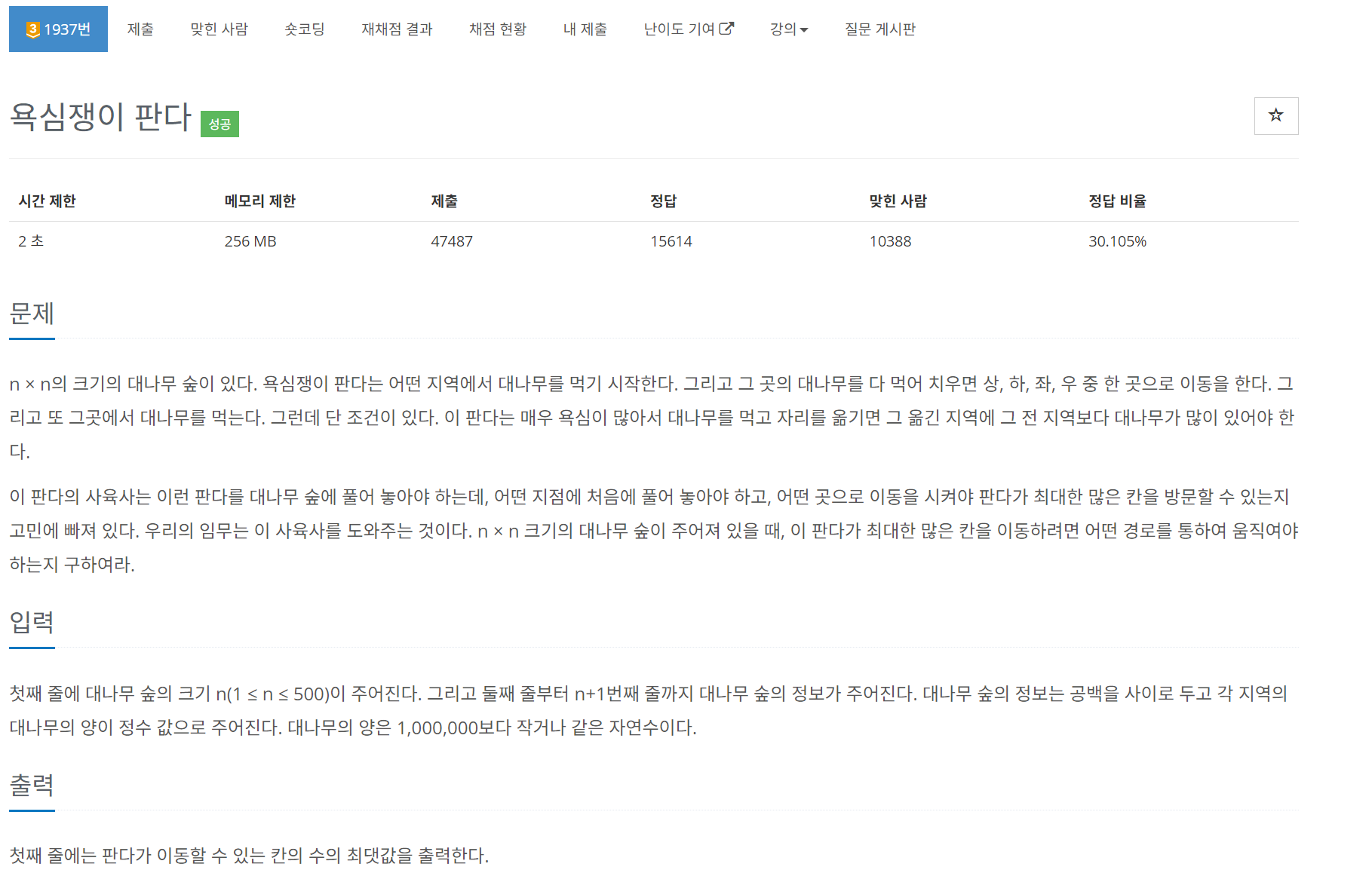
과거 풀었던 비슷한 단계의 내리막길 문제와 유사해 풀이법을 생각해냈다. 대나무가 적힌 map을 입력받고 모든 위치에서의 먹을 수 있는 넓이를 구해야 하기에 처음엔 모든 index에 접근하지만 이전 재귀에서 한번이라도 접근했던 곳은 다시 접근하지 않게 했다.

만약 현재 이미 방문한 기록이 있으면 그 위치에서는 더 발전될 가능성이 없다. 이미 이전 재귀에서 해당 위치보다 대나무 수가 많은 곳은 이미 방문하였기 때문이다.

범위 내 상하좌우에 방문해 현재 대나무보다 많은 곳이 있다면 그곳을 추가 방문한다.

만약 문제 index가 [0][3] 으로 1 2 3 4로 위치한다고 가정하자

맨 처음 1에서 2로 이동하고 2는 자신이 현재 처음방문하였기에 자신의 값을 1로 지정한다.

그 뒤로 2에서 3으로 이동하고 3은 자신이 현재 처음 방문하였기에 자신의 값을 1로 지정한다.

3역시 같은 과정을 반복한다.

4까지 도착했을때 4는 더이상 자신의 위치에서 더 갈 곳이 없다. 자신 주위에는 더이상 대나무 밭이 없거나 자신보다 작은(3)대나무 밭 만이 존재하기 때문이다.

이때 return eat[x][y]로 이전 대나무 밭의 깊이를 정해준다.

1부터 4까지 dfs 후 return이기에 값은 4->1순으로 return된다.
3은 자신의 현재 값(1)과 이전 대나무밭(4)의 크기에 1을 더한것을 비교해 현재 자신의 밭 크기를 정한다.

1을 더한 것으로 비교하는 이유는 4는 현재 자신보다 1칸 더 먹었기 때문이다.

그렇기에 3은 2가 된다.

2는 앞서 3이 한 것과 마찬가지로 자신의 값과 3의 결과 + 1를 비교한다. 이와 같은 과정을 반복하면

1위치의 대나무밭 깊이는 4가 된다.

정답

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

int n;

int map[501][501];
int eat[501][501];
int result = 0;

int dx[4] = { -1,1,0,0 };
int dy[4] = { 0,0,-1,1 };

int dfs(int x, int y) {

	if (eat[x][y] != 0) {
		return eat[x][y];
	}
	//이미 방문한 기록이 있으면 위에서 반환했음
	eat[x][y] = 1;

	//cout << x << " " << y << " " << cur_count << endl;

	for (int i = 0; i < 4; i++) {
		int nx = x + dx[i];
		int ny = y + dy[i];
		if (0 <= nx && nx < n && 0 <= ny && ny < n) {
			if (map[x][y] < map[nx][ny]) {
				eat[x][y] = max(eat[x][y], dfs(nx, ny) + 1);
			}
		}
	}

	return eat[x][y];
}

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	cin >> n;

	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cin >> map[i][j];
		}
	}

	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			if (eat[i][j] == 0) {
				result = max(result, dfs(i, j));
			}
		}
	}

	cout << result;

	return 0;
}