백준 [2565] "전깃줄"

"최소 개수를 구하라" 라는 멘트를 보고 바로 DP 해결법을 생각했다. 두 가지를 해결해야만 했는데

1. 겹치는 줄인 것을 어떻게 찾아낼 것인가?
2. 점화식은 어떻게 구할 것인가

처음 생각해낸 방식은 현재 검사하는 줄을 KA, KB로 놓고 현재 비교 대상인 AB에 대해
a>kx && b<ky, a<kx && b>ky에 대해 검사하고 이를 통해 검사한다. 하지만 이와 같은 방식을 선택했을때 점화식을 생각해내지 못했는데 이유는 1.의 접근 부터 잘못 됐기 때문이였다.

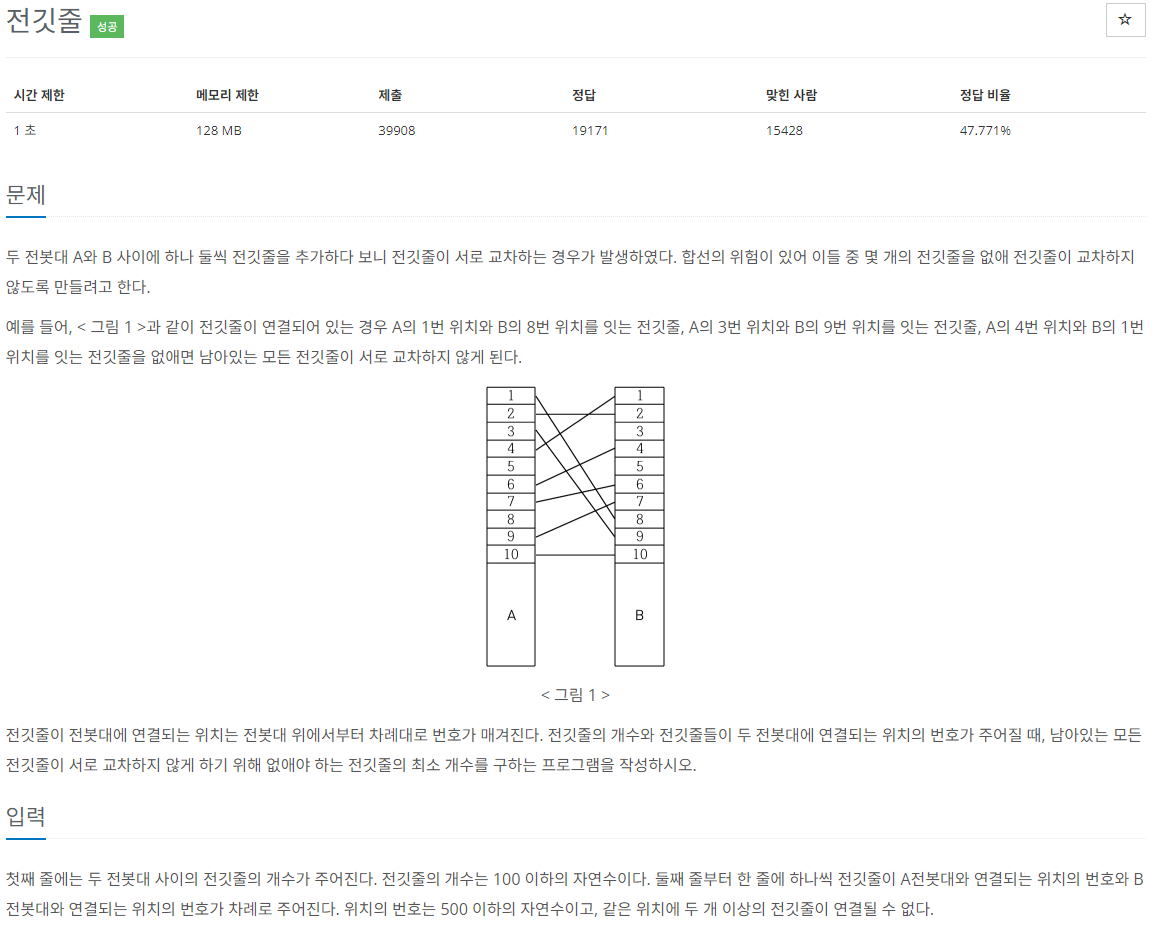
첫 번째 잘못은 정렬하지 않은 것이였다. 문제 예시를 살펴보면 입력을 정렬하지 않고 입력하는 것을 볼 수 있는데 이는 점화식을 할때 옳지 않은 방식이다. 그렇기 때문에 정렬을 먼저 해줘야 한다.

정렬을 하면 자동적으로 A(좌측) 전봇대의 줄이 정렬되기 때문에 B(우측) 전봇대만 고려하면 된다. A 전봇대가 정렬되어 있기 때문에 B 전봇대만 생각하면 현재 I 번째 이은 전봇대의 길이가 저번 J 번째 전봇대보다 숫자가 크다면 겹칠일이 없기 때문에 최장 증가 부분 수열방식을 이용해서 A와 B 전봇대의 최장 증가 부분 수열을 구하고 전체 경우에서 최장 증가 부분 수열의 경우를 빼면 최장 증거에 도움이 되지 않는 불필요한 줄이 나오기 때문에 전체 경우 - 최장 증가 부분 수열 결과를 하면 결과가 나온다.

#include<iostream>
#include<vector>
#include<queue>
#include<stdio.h>
#include<algorithm>

#define endl "\n"

using namespace std;
vector<pair<int, int>> v;
int dp[501];
int res = 0;

int t, n;

void dp_GO() {
	sort(v.begin(), v.end());
	for (int i = 0; i < v.size(); i++) {
		dp[i] = 1;
		for (int j = 0; j < i; j++) {
			if (v[i].second > v[j].second) {
				dp[i] = max(dp[i], dp[j] + 1);
			}
		}
		res = max(dp[i], res);
	}
	cout << n-res << endl;
}

int main()
{
	cin >> n;

	for (int i = 0; i < n; i++) {
		int a, b;
		cin >> a >> b;
		v.push_back({ a,b });
	}

	dp_GO();

	return 0;
}