[Algorithm]Sorting Algorithms(2) - Quick, Merge, Heap Sort

🦊 Quick Sort

👉 Abstract

Quick Sort은 분할 정복(divide and conquer) 방법 을 통해 주어진 배열을 정렬한다.

• [분할 정복(divide and conquer) 방법]
  문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
  Quick Sort은 불안정 정렬에 속하며, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다. 또한 Merge Sort와 달리 Quick Sort는 배열을 비균등하게 분할한다.

👉 Process (Ascending)

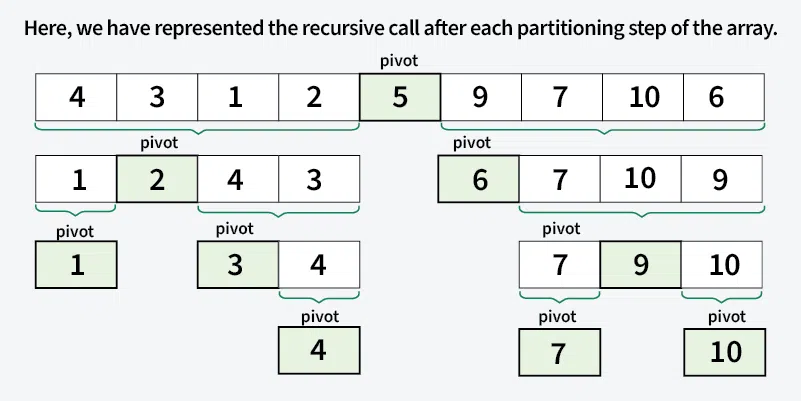
1. 배열 가운데서 하나의 원소를 고른다. 이렇게 고른 원소를 피벗(pivot) 이라고 한다.
2. 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 배열을 둘로 나눈다. 이렇게 배열을 둘로 나누는 것을 분할(Divide) 이라고 한다. 분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다.
3. 분할된 두 개의 작은 배열에 대해 재귀(Recursion)적으로 이 과정을 반복한다.

• 재귀 호출이 한번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.

👉 Code

• 정복 (Conquer)

부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.

• 분할 (Divide)

입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열 (피벗을 중심으로 왼쪽 : 피벗보다 작은 요소들, 오른쪽 : 피벗보다 큰 요소들) 로 분할한다.

1.

# Partition function
def partition(arr, low, high):
    
    # Choose the pivot
    pivot = arr[high]
    
    # Index of smaller element and indicates 
    # the right position of pivot found so far
    i = low - 1
    
    # Traverse arr[low..high] and move all smaller
    # elements to the left side. Elements from low to 
    # i are smaller after every iteration
    for j in range(low, high):
        if arr[j] < pivot:
            i += 1
            swap(arr, i, j)
    
    # Move pivot after smaller elements and
    # return its position
    swap(arr, i + 1, high)
    return i + 1

# Swap function
def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]

# The QuickSort function implementation
def quickSort(arr, low, high):
    if low < high:
        
        # pi is the partition return index of pivot
        pi = partition(arr, low, high)
        
        # Recursion calls for smaller elements
        # and greater or equals elements
        quickSort(arr, low, pi - 1)
        quickSort(arr, pi + 1, high)

# Main driver code
if __name__ == "__main__":
    arr = [10, 7, 8, 9, 1, 5]
    n = len(arr)

    quickSort(arr, 0, n - 1)
    
    for val in arr:
        print(val, end=" ")

2.

def quick_sort(arr):
    if len(arr) <= 1:
        return arr  # 원소가 하나 이하이면 정렬된 상태이므로 그대로 반환
    
    pivot = arr[len(arr) // 2]  # 피벗 선택 (가운데 값)
    left = [x for x in arr if x < pivot]  # 피벗보다 작은 값들
    middle = [x for x in arr if x == pivot]  # 피벗과 같은 값들
    right = [x for x in arr if x > pivot]  # 피벗보다 큰 값들
    
    return quick_sort(left) + middle + quick_sort(right)

# 테스트
arr = [3, 6, 8, 10, 1, 2, 1]
print(quick_sort(arr))  # [1, 1, 2, 3, 6, 8, 10]

👉 시간복잡도

• 최상의 경우: (Ω(n log n)), 피벗 요소가 배열을 두 개의 동일한 부분으로 나눌 때 발생합니다.
• 평균적 경우 (θ(n log n)), 평균적으로 피벗은 배열을 두 부분으로 나누지만 반드시 같지는 않습니다.
• 최악의 경우: (O(n²)), 항상 가장 작은 요소나 가장 큰 요소가 피벗으로 선택되는 경우(예: 정렬된 배열) 발생합니다.

👉 공간복잡도

주어진 배열 안에서 교환(swap)을 통해, 정렬이 수행되므로 O(n)이다.

👉 장점 & 단점

장점

• 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗들이 추후 연산에서 제외되는 특성 때문에, 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
• 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다.

단점

• 불안정 정렬(Unstable Sort) 이다.
• 정렬된 배열에 대해서는 Quick Sort의 불균형 분할에 의해 오히려 수행시간이 더 많이 걸린다.

👉 퀵정렬의 응용

• O(n log n)의 평균 시간 복잡도로 대용량 데이터 세트를 정렬하는 데 효율적입니다.
• k번째로 작은 요소를 찾거나 피벗으로 배열을 나누는 것과 같은 분할 문제에 사용됩니다.
• 무작위 알고리즘에 필수적이며 결정론적 접근 방식보다 더 나은 성능을 제공합니다.
• 암호화에 적용되어 난수 순열과 예측할 수 없는 암호화 키를 생성합니다.
• 다중 코어 또는 분산 시스템의 성능을 향상시키기 위해 분할 단계를 병렬화할 수 있습니다.
• 평균적 복잡성을 분석하고 새로운 기술을 개발하는 이론 컴퓨터 과학에서 중요합니다.

🦊 Merge Sort

👉 Abstract

병합 정렬 은 분할 정복 접근법 을 따르는 정렬 알고리즘입니다 . 입력 배열을 더 작은 하위 배열로 재귀적으로 나누고 해당 하위 배열을 정렬한 다음 다시 병합하여 정렬된 배열을 얻습니다.

간단히 말해서, 병합 정렬 프로세스는 배열을 두 개의 반으로 나누고, 각 반을 정렬한 다음, 정렬된 반을 다시 병합하는 것입니다. 이 프로세스는 전체 배열이 정렬될 때까지 반복됩니다.

-> 퀵소트와는 반대로 안정 정렬에 속함,
-> 요소를 쪼갠 후, 다시 합병시키면서 정렬해나가는 방식으로, 쪼개는 방식은 퀵정렬과 유사

👉 Process

1. 분할: 목록이나 배열을 재귀적으로 두 부분으로 나누어 더 이상 나눌 수 없을 때까지 분할합니다.
2. 정복: 각 부분 배열은 병합 정렬 알고리즘을 사용하여 개별적으로 정렬됩니다.
3. 병합: 정렬된 하위 배열은 정렬된 순서대로 다시 병합됩니다. 이 프로세스는 두 하위 배열의 모든 요소가 병합될 때까지 계속됩니다.

👉 퀵정렬과의 차이점

• 퀵정렬 : 우선 피벗을 통해 정렬(partition) → 영역을 쪼갬(quickSort)

• 합병정렬 : 영역을 쪼갤 수 있을 만큼 쪼갬(mergeSort) → 정렬(merge)

이미 합병의 대상이 되는 두 영역이 각 영역에 대해서 정렬이 되어있기 때문에 단순히 두 배열을 순차적으로 비교하면서 정렬할 수가 있다.

★★★합병정렬은 순차적인 비교로 정렬을 진행하므로, LinkedList의 정렬이 필요할 때 사용하면 효율적이다.★★★

Q. LinkedList를 퀵정렬을 사용해 정렬하면?

성능이 좋지 않음
퀵정렬은, 순차 접근이 아닌 임의 접근이기 때문

LinkedList는 삽입, 삭제 연산에서 유용하지만 접근 연산에서는 비효율적임
따라서 임의로 접근하는 퀵소트를 활용하면 오버헤드 발생이 증가하게 됨

배열은 인덱스를 이용해서 접근이 가능하지만, LinkedList는 Head부터 탐색해야 함
배열[O(1)] vs LinkedList[O(n)]

👉 Code

1.

def merge(arr, left, mid, right):
    n1 = mid - left + 1
    n2 = right - mid

    # Create temp arrays
    L = [0] * n1
    R = [0] * n2

    # Copy data to temp arrays L[] and R[]
    for i in range(n1):
        L[i] = arr[left + i]
    for j in range(n2):
        R[j] = arr[mid + 1 + j]

    i = 0  # Initial index of first subarray
    j = 0  # Initial index of second subarray
    k = left  # Initial index of merged subarray

    # Merge the temp arrays back
    # into arr[left..right]
    while i < n1 and j < n2:
        if L[i] <= R[j]:
            arr[k] = L[i]
            i += 1
        else:
            arr[k] = R[j]
            j += 1
        k += 1

    # Copy the remaining elements of L[],
    # if there are any
    while i < n1:
        arr[k] = L[i]
        i += 1
        k += 1

    # Copy the remaining elements of R[], 
    # if there are any
    while j < n2:
        arr[k] = R[j]
        j += 1
        k += 1

def merge_sort(arr, left, right):
    if left < right:
        mid = (left + right) // 2

        merge_sort(arr, left, mid)
        merge_sort(arr, mid + 1, right)
        merge(arr, left, mid, right)

def print_list(arr):
    for i in arr:
        print(i, end=" ")
    print()

# Driver code
if __name__ == "__main__":
    arr = [12, 11, 13, 5, 6, 7]
    print("Given array is")
    print_list(arr)

    merge_sort(arr, 0, len(arr) - 1)

    print("\nSorted array is")
    print_list(arr)

2.

def merge_sort(arr):
    if len(arr) <= 1:
        return arr  # 리스트 크기가 1 이하이면 정렬 완료

    mid = len(arr) // 2
    left = merge_sort(arr[:mid])  # 왼쪽 반 정렬
    right = merge_sort(arr[mid:])  # 오른쪽 반 정렬
    
    return merge(left, right)  # 정렬된 두 리스트를 병합

def merge(left, right):
    sorted_arr = []
    i = j = 0

    while i < len(left) and j < len(right):  # 두 리스트를 비교하며 정렬
        if left[i] < right[j]:
            sorted_arr.append(left[i])
            i += 1
        else:
            sorted_arr.append(right[j])
            j += 1

    sorted_arr.extend(left[i:])  # 남은 원소 추가
    sorted_arr.extend(right[j:])  # 남은 원소 추가
    return sorted_arr

# 테스트
arr = [3, 6, 8, 10, 1, 2, 1]
print(merge_sort(arr))  # [1, 1, 2, 3, 6, 8, 10]

👉 시간 복잡도

• 최상의 경우: O(n log n), 배열이 이미 정렬되어 있거나 거의 정렬되어 있는 경우.
• 평균적 사례: O(n log n), 배열이 무작위로 정렬된 경우.
• 최악의 경우: O(n log n), 배열이 역순으로 정렬된 경우.

👉 보조 공간

O(n), 병합 중에 사용되는 임시 배열을 위한 추가 공간이 필요합니다.

👉 병합정렬 응용

• 대용량 데이터 세트 정렬
• 외부 정렬 (데이터 세트가 메모리에 맞을 만큼 큰 경우)
• 역 계산
• 병합 정렬과 그 변형은 프로그래밍 언어의 라이브러리 메서드에서 사용됩니다.
  -> TimSort 의 변형은 Python, Java Android 및 Swift에서 사용됩니다. 비원시 유형을 정렬하는 것이 선호되는 주된 이유는 QuickSort에는 없는 안정성 때문입니다.
• 연결 리스트를 정렬하는 데 선호되는 알고리즘입니다.
• 독립적으로 부분 배열을 정렬한 다음 병합할 수 있으므로 쉽게 병렬화할 수 있습니다.
• 병합 정렬의 병합 기능은 두 개의 정렬된 배열의 합집합, 교집합과 같은 문제를 효율적으로 해결합니다 .

👉 병합 정렬의 장점과 단점

장점

• 안정성 : 병합 정렬은 안정적인 정렬 알고리즘으로, 입력 배열에서 동일한 요소의 상대적 순서를 유지합니다.
• 최악의 성능 보장: 병합 정렬은 최악의 시간 복잡도가 O(N logN) 이므로 대규모 데이터 세트에서도 좋은 성능을 보입니다.
• 구현이 간단합니다. 분할 정복 방식은 직관적입니다.
• 자연스러운 병렬 : 병렬 처리에 적합하도록 하위 배열을 독립적으로 병합합니다.

단점

• 공간 복잡도: 병합 정렬은 정렬 과정에서 병합된 하위 배열을 저장하기 위해 추가 메모리가 필요합니다.
• 제자리 정렬이 아님: 병합 정렬은 제자리 정렬 알고리즘이 아니므로 정렬된 데이터를 저장하기 위해 추가 메모리가 필요합니다. 이는 메모리 사용량이 문제가 되는 애플리케이션에서 단점이 될 수 있습니다.
• 병합 정렬은 일반적으로 퀵 정렬보다 느립니다. 퀵 정렬은 제자리에서 작동하기 때문에 캐시에 더 친화적입니다.

🦊 Heap Sort

👉 Abstract

힙 정렬 은 이진 힙 데이터 구조 에 기반한 힙(Heap) 자료구조를 기반으로한 비교 기반 정렬 기술입니다.

선택 정렬 에 대한 최적화로 볼 수 있는데 , 먼저 최대(또는 최소) 요소를 찾아서 마지막(또는 첫 번째) 요소와 바꿉니다. 나머지 요소에 대해서도 같은 과정을 반복합니다.
힙 정렬에서는 이진 힙을 사용하여 O(n) 대신 O(Log n)에서 최대 요소를 빠르게 찾아 이동할 수 있으므로 O(n Log n) 시간 복잡도를 달성합니다.

Q. 완전 이진 트리란?

삽입할 때 왼쪽부터 차례대로 추가하는 이진 트리

👉 Process

1단계: 배열을 완전한 이진 트리로 취급

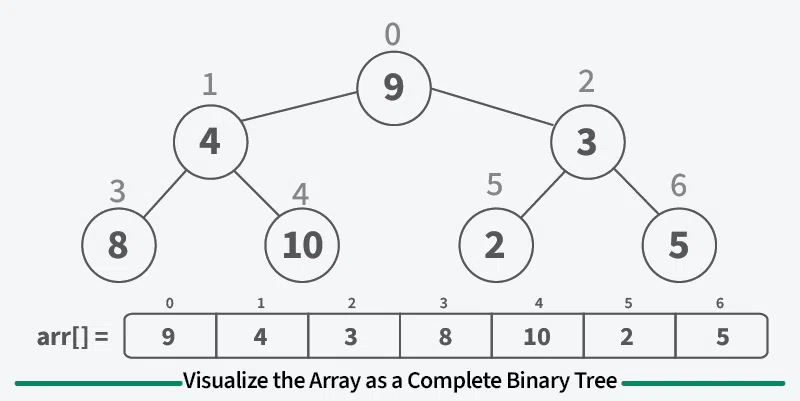
2단계: 최대 힙 구축
3단계: 정렬되지 않은 배열의 끝에 가장 큰 요소를 배치하여 배열을 정렬합니다.
힙에 하나의 요소만 남을 때까지 이러한 단계를 계속 반복해야 합니다.

1. 최대 힙을 구성
2. 현재 힙 루트는 가장 큰 값이 존재함. 루트의 값을 마지막 요소와 바꾼 후, 힙의 사이즈 하나 줄임
3. 힙의 사이즈가 1보다 크면 위 과정 반복
   
   
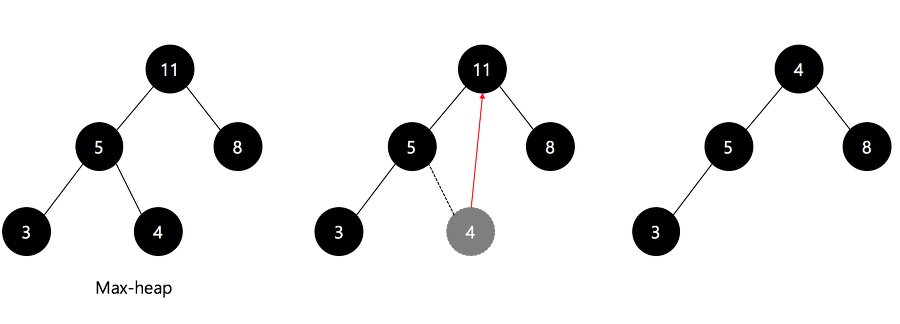
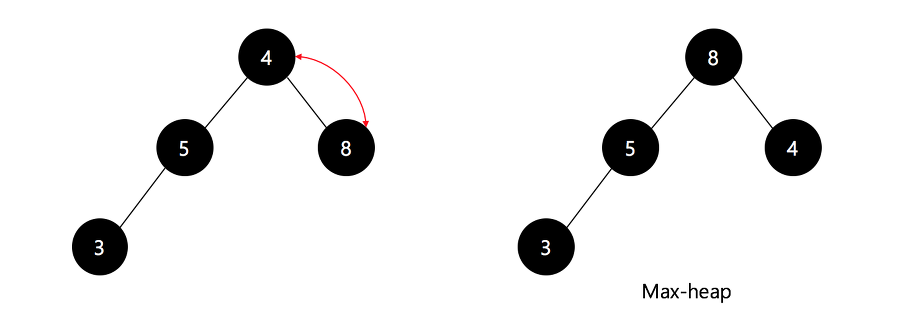
   이와 같은 방식으로 최대 값을 하나씩 뽑아내면서 정렬하는 것이 힙 소트

👉 Code

1.

# Python program for implementation of heap Sort

# To heapify a subtree rooted with node i
# which is an index in arr[].
def heapify(arr, n, i):
    
     # Initialize largest as root
    largest = i 
    
    #  left index = 2*i + 1
    l = 2 * i + 1 
    
    # right index = 2*i + 2
    r = 2 * i + 2  

    # If left child is larger than root
    if l < n and arr[l] > arr[largest]:
        largest = l

    # If right child is larger than largest so far
    if r < n and arr[r] > arr[largest]:
        largest = r

    # If largest is not root
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # Swap

        # Recursively heapify the affected sub-tree
        heapify(arr, n, largest)

# Main function to do heap sort
def heapSort(arr):
    
    n = len(arr) 

    # Build heap (rearrange array)
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    # One by one extract an element from heap
    for i in range(n - 1, 0, -1):
      
        # Move root to end
        arr[0], arr[i] = arr[i], arr[0] 

        # Call max heapify on the reduced heap
        heapify(arr, i, 0)

def printArray(arr):
    for i in arr:
        print(i, end=" ")
    print()

# Driver's code
arr = [9, 4, 3, 8, 10, 2, 5] 
heapSort(arr)
print("Sorted array is ")
printArray(arr)

2. Python의 heapq 모듈은 기본적으로 최소 힙(Min Heap)을 제공

def heap_sort(arr):
    import heapq
    heapq.heapify(arr)  # 리스트를 최소 힙으로 변환
    return [heapq.heappop(arr) for _ in range(len(arr))]  # 힙에서 하나씩 꺼내 정렬

# 테스트
arr = [3, 6, 8, 10, 1, 2, 1]
print(heap_sort(arr))  # [1, 1, 2, 3, 6, 8, 10]

3.최대 힙(Max Heap)을 직접 구현하여 힙 정렬을 수행 가능

def heapify(arr, n, i):
    largest = i  # 루트 노드
    left = 2 * i + 1  # 왼쪽 자식 노드
    right = 2 * i + 2  # 오른쪽 자식 노드

    # 왼쪽 자식이 루트보다 크다면
    if left < n and arr[left] > arr[largest]:
        largest = left

    # 오른쪽 자식이 현재 최대값보다 크다면
    if right < n and arr[right] > arr[largest]:
        largest = right

    # 최대값이 루트가 아니라면 스왑 후 다시 힙 속성을 유지하도록 호출
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)  # 재귀 호출

def heap_sort(arr):
    n = len(arr)

    # 1. 최대 힙(Max Heap) 만들기 (Heapify 과정)
    for i in range(n // 2 - 1, -1, -1):  # 내부 노드부터 힙 속성을 만족하도록 변환
        heapify(arr, n, i)

    # 2. 정렬 과정 (Heap Sort)
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # 최대값(루트)와 마지막 요소를 교환
        heapify(arr, i, 0)  # 루트에 대해 다시 Heapify 수행

    return arr

# 테스트
arr = [3, 6, 8, 10, 1, 2, 1]
print(heap_sort(arr))  # [1, 1, 2, 3, 6, 8, 10]

👉 힙 소트가 유용할 때

• 가장 크거나 가장 작은 값을 구할 때

-> 최소 힙 or 최대 힙의 루트 값이기 때문에 한번의 힙 구성을 통해 구하는 것이 가능

• 최대 k 만큼 떨어진 요소들을 정렬할 때

-> 삽입정렬보다 더욱 개선된 결과를 얻어낼 수 있음

👉 힙 정렬 의 복잡도

• 시간 복잡도: O(n log n)
• 보조 공간: 재귀적 호출 스택으로 인해 O(log n). 그러나 보조 공간은 반복 구현의 경우 O(1)이 될 수 있습니다.

👉 Heap Sort에 대한 중요한 점

• 힙 정렬은 제자리 알고리즘입니다.
• 일반적인 구현은 안정적이지 않지만 안정적으로 만들 수 있습니다
• 일반적으로 잘 구현된 QuickSort 보다 2-3배 느립니다 . 느린 이유는 참조 지역성이 부족하기 때문입니다.

👉 힙 정렬의 장단점

힙 정렬의 장점

• 효율적인 시간 복잡도: 힙 정렬은 모든 경우에 O(n log n)의 시간 복잡도를 갖습니다. 이는 대규모 데이터 세트를 정렬하는 데 효율적입니다. log n 요소는 이진 힙의 높이에서 나오며, 이는 알고리즘이 많은 수의 요소에서도 좋은 성능을 유지하도록 보장합니다.
• 메모리 사용: 메모리 사용은 최소화할 수 있습니다(재귀적 heapify() 대신 반복적 heapify()를 작성하여). 따라서 정렬할 항목의 초기 목록을 보관하는 데 필요한 것 외에는 작동하기 위해 추가 메모리 공간이 필요하지 않습니다.
• 단순성: 재귀와 같은 고급 컴퓨터 과학 개념을 사용하지 않기 때문에 다른 동등한 효율성의 정렬 알고리즘보다 이해하기가 더 간단합니다.

힙 정렬의 단점

• 비용 : 힙 정렬은 병합 정렬보다 상수가 더 높기 때문에 비용이 많이 듭니다. 두 정렬 모두 시간 복잡도가 O(n Log n)입니다.
• 불안정 : 힙 정렬은 불안정합니다. 상대적 순서를 재정렬할 수 있습니다.
• 비효율성: 힙 정렬은 시간 복잡도가 높기 때문에 그다지 효율적이지 않습니다.

정리

• 빠른 정렬이 필요하면? → 퀵 정렬
• 안정 정렬이 필요하면? → 병합 정렬
• 제자리 정렬이 필요하면? → 힙 정렬

정렬알고리즘 평균 시간 복잡도 최악 시간 복잡도 공간 복잡도 특징
퀵 정렬 (Quick Sort) O(n log n) O(n²) (최악: 이미 정렬된 경우) O(n) (비효율적 구현) 분할 정복, 빠름
병합 정렬 (Merge Sort) O(n log n) O(n log n) O(n) 안정 정렬, 일관된 성능
힙 정렬 (Heap Sort) O(n log n) O(n log n) O(1) 제자리 정렬 가능