Sorting Algorithms
정렬은 주어진 배열이나 요소의 목록을 요소에 대한 비교 연산자에 따라 재배열하는 것을 말합니다. 비교 연산자는 해당 데이터 구조에서 요소의 새로운 순서를 결정하는 데 사용됩니다.
정렬 기술의 종류
데이터 구조에는 다양한 정렬 알고리즘이 사용됩니다. 다음 두 가지 유형의 정렬 알고리즘은 광범위하게 분류할 수 있습니다.
비교 기반: 비교 기반 정렬 알고리즘에서 요소를 비교합니다.
비교 기반이 아님: 비교 기반이 아닌 정렬 알고리즘에서는 요소를 비교하지 않습니다.
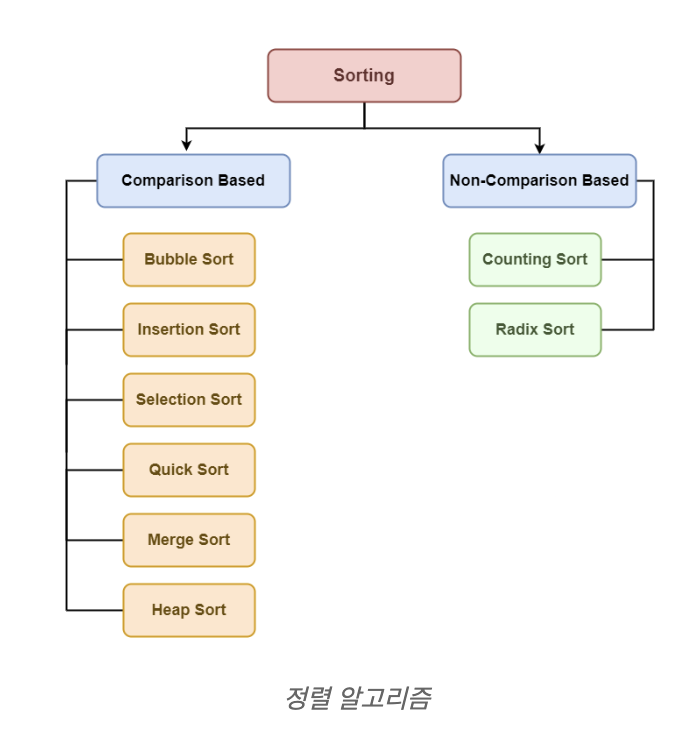
정렬 알고리즘:
- 비교 기반 : 선택 정렬 , 버블 정렬 , 삽입 정렬 , 병합 정렬 , 퀵 정렬 , 힙 정렬 , 사이클 정렬 , 3방향 병합 정렬
- 비교 기반이 아닌 : 카운팅 정렬 , 라딕스 정렬 , 버킷 정렬 , 팀 정렬 , 빗살 정렬 , 비둘기집 정렬
- 하이브리드 정렬 알고리즘 : 인트로 정렬 , 팀 정렬
🦋 버블 정렬(Bubble Sort Algorithm)
버블 정렬 은 인접한 요소가 잘못된 순서로 되어 있으면 반복적으로 스왑하여 작동하는 가장 간단한 정렬 알고리즘입니다. 이 알고리즘은 평균 및 최악의 경우 시간 복잡도가 매우 높기 때문에 대규모 데이터 세트에 적합하지 않습니다.
👉 Process (Ascending)
- 1회전에 첫 번째 원소와 두 번째 원소를, 두 번째 원소와 세 번째 원소를, 세 번째 원소와 네 번째 원소를, … 이런 식으로 (마지막-1)번째 원소와 마지막 원소를 비교하여 조건에 맞지 않는다면 서로 교환한다.
- 1회전을 수행하고 나면 가장 큰 원소가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 원소는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두 번째 원소까지는 정렬에서 제외된다. 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어난다
1.
# Optimized Python program for implementation of Bubble Sort
def bubbleSort(arr):
n = len(arr)
# Traverse through all array elements
for i in range(n):
swapped = False
# Last i elements are already in place
for j in range(0, n-i-1):
# Traverse the array from 0 to n-i-1
# Swap if the element found is greater
# than the next element
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
swapped = True
if (swapped == False):
break
# Driver code to test above
if __name__ == "__main__":
arr = [64, 34, 25, 12, 22, 11, 90]
bubbleSort(arr)
print("Sorted array:")
for i in range(len(arr)):
print("%d" % arr[i], end=" ")2.
def bubble_sort(arr):
n = len(arr)
for i in range(n):
swapped = False
for j in range(n - i - 1): # 마지막 i개 요소는 이미 정렬됨
if arr[j] > arr[j + 1]: # 인접한 두 값 비교 후 스왑
arr[j], arr[j + 1] = arr[j + 1], arr[j]
swapped = True
if not swapped: # 정렬이 완료되면 조기 종료
break
return arr
# 테스트
arr = [5, 1, 4, 2, 8]
print(bubble_sort(arr)) # [1, 2, 4, 5, 8]시간복잡도
- 시간복잡도를 계산하면, (n-1) + (n-2) + (n-3) + .... + 2 + 1 => n(n-1)/2이므로, O(n^2) 이다. 또한, Bubble Sort는 정렬이 돼있던 안돼있던, 2개의 원소를 비교하기 때문에 최선, 평균, 최악의 경우 모두 시간복잡도가 O(n^2) 으로 동일하다. (개선된 Bubble Sort가 존재하긴 하나, 기초를 다지기 위한 학습이므로 넘어가겠음)
공간복잡도
- 주어진 배열 안에서 교환(swap)을 통해, 정렬이 수행되므로 O(n) 이다.
장점
- 구현이 매우 간단하고, 소스코드가 직관적이다.
- 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않다. => 제자리 정렬(in-place sorting)
- 안정 정렬(Stable Sort) 이다.
단점
- 시간복잡도가 최악, 최선, 평균 모두 O(n^2)으로, 굉장히 비효율적이다.
- 정렬 돼있지 않은 원소가 정렬 됐을때의 자리로 가기 위해서, 교환 연산(swap)이 많이 일어나게 된다.
🦋 선택 정렬(Selection Sort)
선택 정렬은 비교 기반 정렬 알고리즘입니다. 정렬되지 않은 부분에서 가장 작은(또는 가장 큰) 요소를 반복적으로 선택하여 첫 번째 정렬되지 않은 요소와 교환하여 배열을 정렬합니다. 이 프로세스는 전체 배열이 정렬될 때까지 계속됩니다.
👉 Process (Ascending)
- 1회전에 첫 번째 원소와 두 번째 원소를, 두 번째 원소와 세 번째 원소를, 세 번째 원소와 네 번째 원소를, … 이런 식으로 (마지막-1)번째 원소와 마지막 원소를 비교하여 조건에 맞지 않는다면 서로 교환한다.
- 1회전을 수행하고 나면 가장 큰 원소가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 원소는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두 번째 원소까지는 정렬에서 제외된다. 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어난다
1.
# Python program for implementation of Selection
# Sort
def selection_sort(arr):
n = len(arr)
for i in range(n - 1):
# Assume the current position holds
# the minimum element
min_idx = i
# Iterate through the unsorted portion
# to find the actual minimum
for j in range(i + 1, n):
if arr[j] < arr[min_idx]:
# Update min_idx if a smaller element is found
min_idx = j
# Move minimum element to its
# correct position
arr[i], arr[min_idx] = arr[min_idx], arr[i]
def print_array(arr):
for val in arr:
print(val, end=" ")
print()
if __name__ == "__main__":
arr = [64, 25, 12, 22, 11]
print("Original array: ", end="")
print_array(arr)
selection_sort(arr)
print("Sorted array: ", end="")
print_array(arr)2.
def selection_sort(arr):
n = len(arr)
for i in range(n - 1):
min_idx = i # 최소값 인덱스 초기화
for j in range(i + 1, n):
if arr[j] < arr[min_idx]: # 더 작은 값을 찾으면 인덱스 업데이트
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i] # 최소값을 현재 위치와 교환
return arr
# 테스트
arr = [64, 25, 12, 22, 11]
print(selection_sort(arr)) # [11, 12, 22, 25, 64]시간복잡도
데이터의 개수가 n개라고 했을 때,
- 첫 번째 회전에서의 비교횟수 : 1 ~ (n-1) => n-1
- 두 번째 회전에서의 비교횟수 : 2 ~ (n-1) => n-2
...
- (n-1) + (n-2) + .... + 2 + 1 => n(n-1)/2
비교하는 것이 상수 시간에 이루어진다는 가정 아래, n개의 주어진 배열을 정렬하는데 O(n^2) 만큼의 시간이 걸린다. 최선, 평균, 최악의 경우 시간복잡도는 O(n^2) 으로 동일하다.
공간복잡도
- 주어진 배열 안에서 교환(swap)을 통해, 정렬이 수행되므로 O(n) 이다.
장점
- Bubble sort와 마찬가지로 알고리즘이 단순하다.
- 정렬을 위한 비교 횟수는 많지만, Bubble Sort에 비해 실제로 교환하는 횟수는 적기 때문에 많은 교환이 일어나야 하는 자료상태에서 비교적 효율적이다.
- Bubble Sort와 마찬가지로 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다. => 제자리 정렬(in-place sorting)
단점
- 시간복잡도가 O(n^2)으로, 비효율적이다.
- 불안정 정렬(Unstable Sort) 이다.
🦋 삽입 정렬(Insertion Sort)
삽입 정렬 은 정렬되지 않은 목록의 각 요소를 목록의 정렬된 부분에서 올바른 위치에 반복적으로 삽입하여 작동하는 간단한 정렬 알고리즘입니다.
손에 든 카드를 정렬하는 것과 같습니다. 카드를 정렬된 카드와 정렬되지 않은 카드의 두 그룹으로 나눕니다. 그
런 다음 정렬되지 않은 그룹에서 카드를 하나 골라 정렬된 그룹의 올바른 위치에 놓습니다.
Insertion Sort는 2번째 원소부터 시작하여 그 앞(왼쪽)의 원소들과 비교하여 삽입할 위치를 지정한 후, 원소를 뒤로 옮기고 지정된 자리에 자료를 삽입 하여 정렬하는 알고리즘이다.
최선의 경우 O(N)이라는 엄청나게 빠른 효율성을 가지고 있어, 다른 정렬 알고리즘의 일부로 사용될 만큼 좋은 정렬 알고리즘이다.
Process (Ascending)
- 정렬은 2번째 위치(index)의 값을 temp에 저장한다.
- temp와 이전에 있는 원소들과 비교하며 삽입해나간다.
- '1'번으로 돌아가 다음 위치(index)의 값을 temp에 저장하고, 반복한다.
1.
# Python program for implementation of Insertion Sort
# Function to sort array using insertion sort
def insertionSort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
# Move elements of arr[0..i-1], that are
# greater than key, to one position ahead
# of their current position
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
# A utility function to print array of size n
def printArray(arr):
for i in range(len(arr)):
print(arr[i], end=" ")
print()
# Driver method
if __name__ == "__main__":
arr = [12, 11, 13, 5, 6]
insertionSort(arr)
printArray(arr)2.
def insertion_sort(arr):
n = len(arr)
for i in range(1, n):
key = arr[i] # 현재 삽입할 값
j = i - 1
while j >= 0 and arr[j] > key: # key보다 큰 값은 한 칸씩 뒤로 이동
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key # 적절한 위치에 key 삽입
return arr
# 테스트
arr = [12, 11, 13, 5, 6]
print(insertion_sort(arr)) # [5, 6, 11, 12, 13]시간복잡도
최악의 경우(역으로 정렬되어 있을 경우) Selection Sort와 마찬가지로, (n-1) + (n-2) + .... + 2 + 1 => n(n-1)/2 즉, O(n^2) 이다.
하지만, 모두 정렬이 되어있는 경우(Optimal)한 경우, 한번씩 밖에 비교를 안하므로 O(n) 의 시간복잡도를 가지게 된다. 또한, 이미 정렬되어 있는 배열에 자료를 하나씩 삽입/제거하는 경우에는, 현실적으로 최고의 정렬 알고리즘이 되는데, 탐색을 제외한 오버헤드가 매우 적기 때문이다.
최선의 경우는 O(n) 의 시간복잡도를 갖고, 평균과 최악의 경우 O(n^2) 의 시간복잡도를 갖게 된다.
공간복잡도
주어진 배열 안에서 교환(swap)을 통해, 정렬이 수행되므로 O(n) 이다.
장점
- 알고리즘이 단순하다.
- 대부분의 원소가 이미 정렬되어 있는 경우, 매우 효율적일 수 있다.
- 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다. => 제자리 정렬(in-place sorting)
- 안정 정렬(Stable Sort) 이다.
- Selection Sort나 Bubble Sort과 같은 O(n^2) 알고리즘에 비교하여 상대적으로 빠르다.
단점
- 평균과 최악의 시간복잡도가 O(n^2)으로 비효율적이다.
- Bubble Sort와 Selection Sort와 마찬가지로, 배열의 길이가 길어질수록 비효율적이다.
