0. Intro

직관적인 개념을 공식화할 때 일반적인 접근 방법은 객체의 집합과 이러한 객체들을 조작하는 규칙들을 구성하는 것이고, 이것은 대수학으로 알려져 있다. 선형대수학은 벡터와 벡터를 조작하기 위한 특정 규칙에 대해 연구한다. 대부분 사람들이 알고 있는 벡터는 기하학적 벡터이며 일반적으로 문자 위에 작은 화살표로 표시된다.

일반적으로 벡터는 스칼라는 더하거나 곱하여 같은 종류의 다른 객체를 생성할 수 있는 특수한 객체로 추상적인 수학적 관점에서 이를 만족하는 객체는 벡터로 간주할 수 있다.

벡터의 예시를 몇가지 들어보면

1. Geometric vectors(기하학적 벡터)

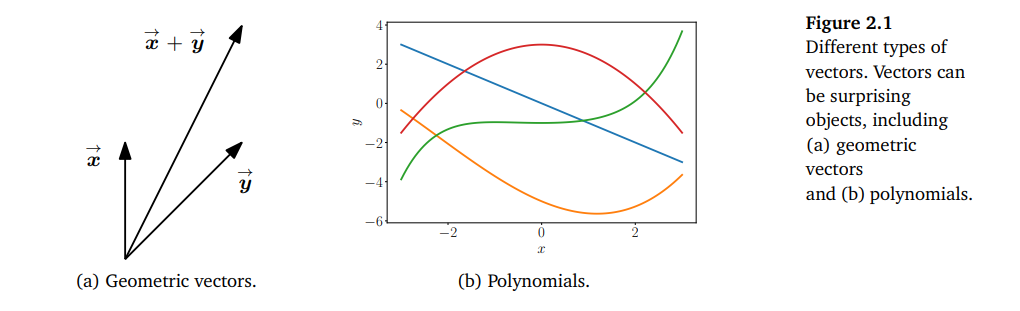
기하학적 벡터는 아래에 있는 Figure2.1의 (a)와 같다. 방향이 있으며, 적어도 2차원으로 구성되어 있습니다. 그림에서 볼 수 있듯이, 두 기하학적 벡터 $\overrightarrow{x}$, $\overrightarrow{y}$는 더할 수 있으며,
$\overrightarrow{x}$ + $\overrightarrow{y}$ = $\overrightarrow{z}$와 같이 새로운 기하하적 벡터를 생성한다. 또한 λ$\overrightarrow{x}$, λ∈R 과 같이 스칼라로 곱한 결과 역시 기하학적 벡터이다. 따라서 벡터를 기하학적으로 해석하면 연산을 방향과 크기에 대해 직관적으로 추론할 수 있다.

2. Polynomials

Figure 2.1의 (b)와 같은 다항식 또한 벡터로 두 다항식을 더할 수 있고, 이는 새로운 다항식을 생성한다. 그리고 스칼라 값 λ∈R 을 곱한 결과 역시 새로운 다항식이다. 기하학적 벡터는 구체적인 개념인 반면, 다항식은 좀 더 추상적인 개념이다.

3. Audio signals

오디오 신호도 벡터인데 오디오 신호는 일련의 숫자로 표현할 수 있으며, 오디오 신호끼리 서로 더할 수 있고, 더한 결과는 새로운 오디오 신호가 된다. 또한, 오디오의 크기를 바꾸면(scaling) 새로운 오디오 신호를 얻을 수 있다.

Elements of $R^n$

n차원의 튜플도 벡터이다. $R^n$ 은 다항식보다 좀 더 추상적인며, 이 책에서는 포커스를 맞추는 개념이다. 예를 들어,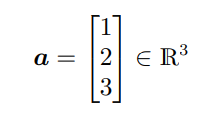
은 숫자들의 triplet을 보여준다. 두 벡터 a, b ∈ $R^n$ 를 각 성분끼리 더하면 새로운 벡터 c = a + b, c ∈ $R^n$를 얻는다. 또한 a에 스칼라λ를 곱하여 스케일링한 값 또한 λa ∈ $R^n$ 이 된다. 벡터를 $R^n$의 원소로 취급하면 컴퓨터에서 실수들의 배열로 처리할 수 있는 추가적인 이점이 있다.

선형대수학은 위와 같은 벡터 개념 간의 유사성에 집중하는데, 이들은 서로 더하거나 스칼라로 곱할 수 있다. 선형대수학에서 대부분의 알고리즘은 $R^n$에서 공식화되기 때문에 $R^n$에서의 벡터에 중점을 둔다.

수학에서 중요한 개념 중 하나는 ‘닫힘(closer)’이라는 개념입니다. 닫힘이라는 개념은 다음와 같은 질문으로 표현할 수 있다.

"내가 수행한 어떠한 연산으로 인해 발생할 수 있는 모든 것들의 집합은 무엇인가 ? 벡터의 경우에는, 작은 벡터 집합에서 이들을 더하거나 스케일링하여 얻을 수 있는 벡터 집합은 무엇인가?"

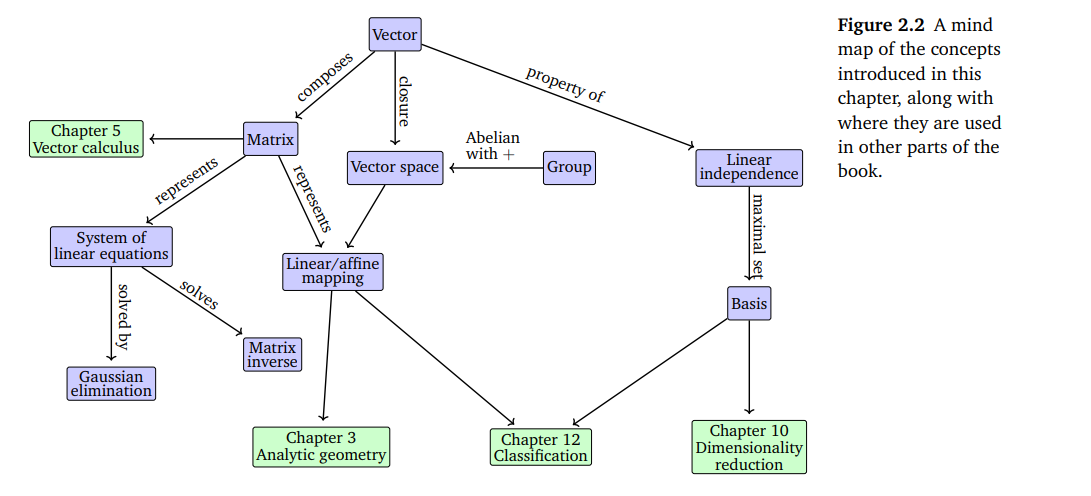
위와 같은 질문에서 언급한 연산을 통해서 결과적으로는 벡터 공간이 생성되며, 이는 2.4절에서 살펴보자. 벡터 공간의 개념과 그 성질은 머신 러닝의 기초가 되며 2장에서 소개되는 개념들은 아래 그림과 같습니다.