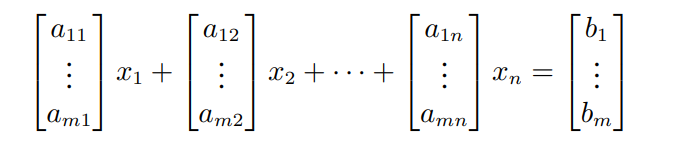연립선형방정식은 선형대수학의 중심이 되는 부분이다.
예시를 들어 설명하자면 회사A가 제품을 생산할 때 각각 의 자원이 필요하다고 할 때 는 라는 제품 하나를 생산하기 위한 자원 를 표현한다.(i=1,...,m and j = 1,....,n)
총 만큼의 자원을 사용할 수 있을 때, 남는 자원 없이 최대 생산가능 수를 찾으면 각 제품 갯수를 라고 하면 다음과 같은 연립방정식을 만족한다.
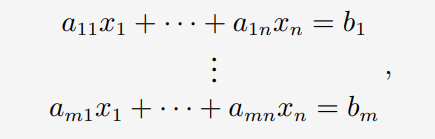
위 식은 연립선형방정식의 general form이고 은 미지의 값이고 위의 방정식의 해이다.
연립선형방정식의 해는 하나도 없거나 오직 하나거나 무한히 많은 해를 얻을 수 있다.
2개의 변수에서 연립방정식의 해는 두 직선의 교집합이므로 가능한 교집합은 직선(두 직선이 동일), 점, 공집합(두 직선이 평행)이 될 수 있다.
나아가 3개의 변수에서 연립방정식의 해는 3차원 공간 평면의 교집합이므로 가능한 교집합은 평면, 직선 점 또는 공집합이 될 수 있다.
위의 연립방정식의 general form은 다음과 같이 행렬로 표현가능하다.