Ch 4-1. Determinant and Trace

Determinant

행렬식은 분석을 위한 수학적 도구이면서 선형연립방정식의 솔루션으로 매우 중요한 개념이다. 행렬식은 오직 정사각행렬에 대해서만 정의된다. 행렬식은 $det(A)$ 또는 $∣A∣$로 표현한다.

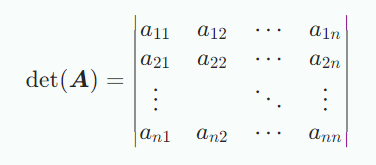
행렬식은 정사각행렬을 실수로 매핑하는 함수로 볼 수 있다.

정사각행렬 $A$가 역행렬이 존재한다고 할 때, 1 X 1 행렬이면, $A=a ⟹ A^{-1}=$ $1\over a$이다.
2 X 2행렬인 경우 $AA^{−1}=I$이므로 A의 역행렬은 다음과 같다.

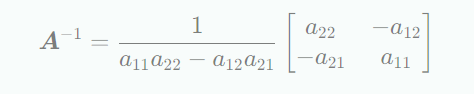
그러므로 $a_{11}a_{22} - a_{12}a_{21}$가 0이 아닐 때 $A$의 역행렬이 존재한다. 여기서 $a_{11}a_{22} - a_{12}a_{21}$가 $A∈R^{2×2}$의 행렬식이다.

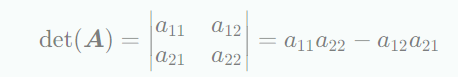
모든 정사각행렬은 $A$에 대해 $det(A)$가 0이 아닐 때, $A$의 역행렬이 존재한다.
n = 1경우 $det(A)=a_{11}$이며 n = 2일 때, $det(A)=a_{11}a_{22} - a_{12}a_{21}$이다. n = 3인 경우는 Sarrus’ rule이며 다음과 같다.

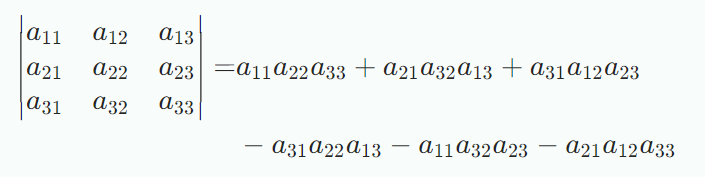
위 식을 쉽게 기억하려면 행렬의 삼중곱을 기억하면 된다.

정사각 행렬 $T$가 대각 요소의 위 또는 아래 부분이 모두 0인 삼각행렬일 때, 행렬식은 대각요소들의 곱이며 다음과 같다.

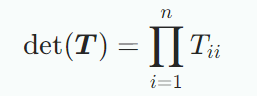
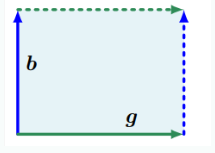
$det(A)$는 행렬 A의 열들로 형성된 n-차원 평행육면체의 부호가 있는 부피다. 예시로 n이 2일 때, 행렬의 열들은 평행사변형을 형성한다. 두 벡터 사이의 각도가 작아질수록 평행사변형의 넓이도 줄어든다. 행렬의 행렬식의 절대값은 평행사변형의 넓이가 된다. 만약 두 벡터가 선형종속이면 $b=λg, λ∈R$이고 넓이는 0이다. 선형독립이라면 두 벡터는 canonical basis벡터의 배수로 표현가능하며 행렬식은 $bg - 0=bg$가 된다.

3차원으로 확장하면 $R^3$에서 3개의 벡터 $r, b, g$가 존재할 때, 이 벡터들은 평행육면체의 edges를 span한다. 육면체의 모양은 다음과 같다.

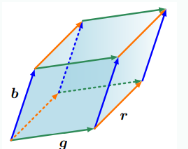
r,g,b 세 벡터는 다음과 같이 행렬의 열로 구성될 수 있고 부피는 $V=∣det(A)∣=186$가 된다.
즉 행렬식은 해당 행렬을 linear transformation으로 볼 때, 변환되는 영역이 어떻게 scaling되는지 알려주는 요소로 행렬식의 부호는 방향을 의미한다.

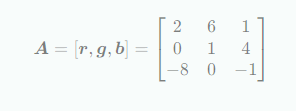
n X n 행렬의 행렬식 계산은 (n−1)×(n−1) 행렬식의 계산으로 축소 가능하다. 이것을 Laplace expansion이라고 하며 이를 2×2 행렬의 행렬식을 구할 때까지 반복 수행하여 n X n행렬의 행렬식을 계산한다.

행렬 $A∈R^{n×n}$가 있을 때, j = 1, ...,n에 대하여
1. 열 j에 관한 expansion

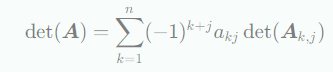
2. 행 j에 관한 expansion
   

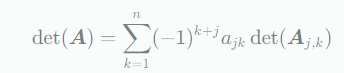
여기서 $A_{k,j}∈R^{(n−1)×(n−1)}$는 k행과 j열을 제거하여 얻은 $A$ 의 부분행렬이다.

$A∈R^{n×n}$에 대한 행렬식은 다음과 같은 속성들을 가진다.