Mathematics for Machine Learning

Bottom-up개념을 기본적인 것에서 점차 깊게 들어가는 방식으로 이방법은 이전에 배운 개념들에 의존하기 때문에 가장 선호되는 접근 방식이나 이러한 방식은 동기부여가 부족하여 대부분의 기본개념들을 빠르게 잊어버리게 될 수 있다.Top-down실용적인 요구에 의해 먼저

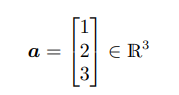
기하학적 벡터는 우리에게 가장 친숙한 벡터로 두개의 기하학적 벡터를 더하면 또다른 기하학적벡터가 되고특정 벡터에 스칼라값을 곱해도 계속 기하학적 벡터의 형태를 띈다.다항식 또한 백터라고 할 수 있는데 두개의 서로 다른 다항식을 더하면 또다른 다항식이 되고 다항식에 스칼

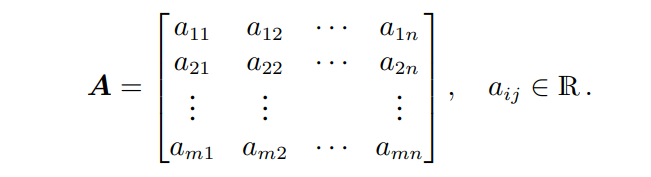
행렬은 선형대수학에서 매운 중요하며, 연립선형방정식을 간결히 표현하는데에 사용된다.다음과 같은 행렬 A는 m,n 튜플로 표현되는 실수 $a{ij}$를 요소로 가지며 m개의 행과 n개의 열로 구성된다. 행과 열은 행벡터, 열벡터라고도 부른다.행렬A는 모든 열을 일렬로 쌓

다음의 세단계을 통하여 특수해와 일반해를 구할 수 있다.1\. $Ax=b$ 에서 특수해(particular solution)을 구한다.2\. $Ax=0$ 에서 모든 해를 구한다.3\. 1과 2를 통해 얻은 해를 결합하여 일반해(general solution)을 구한다.

집합 G과 연산 ⊗:G×G→G 가 G 에 대해 정의되어 있을 때, 아래의 조건을 만족하는 $G$:=(G,⊗)를 군이라고 부른다.위의 조건에 추가로 $∀x,y∈G:x⊗y=y⊗x$(교환법칙)를 만족하면 해당 그룹을 아벨군이라고 한다.역행렬이 존재하는 regular matr

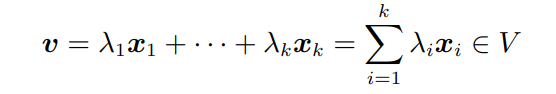
아래의 형태를 만족하는 모든 v를 벡터 $x_1, ...., .x_k$의 선형결합이라고 한다.0벡터는 항상 선형결합을 표현이 가능하다. 여기서 우리는 계수가 전부 0이 아닌(자명하지않은) 선형결합을 찾는 것이 목적이다.v = 0에서 계수가 하나라도 0이 아니라면 $x

벡터공간 $V$ = $($V$, +, ⋅)$와 벡터집합 A = {$x_1, ...., x_k$} ⊆ V에서 V에 속하는 모든 벡터 $v$가 A의 벡터들의 선형결합으로 표현될 때 집합 A를 $V$의 생성집합이라고 하며 A에 속하는 벡터들의 모든 선형결합 집합을 A의 sp

Linear Mappings

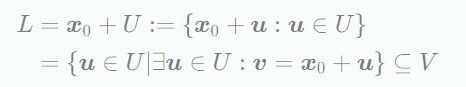
$V$가 벡터공간이고 $x_0 ∈ V$ 이고 $U⊆V$일 때, 다음과 같은 subset $L$은 $V$의 affine subspaces 또는 linear manifold라고 부르며 U 는 direction 또는 direction space 라고 하며, $x_0$은 s

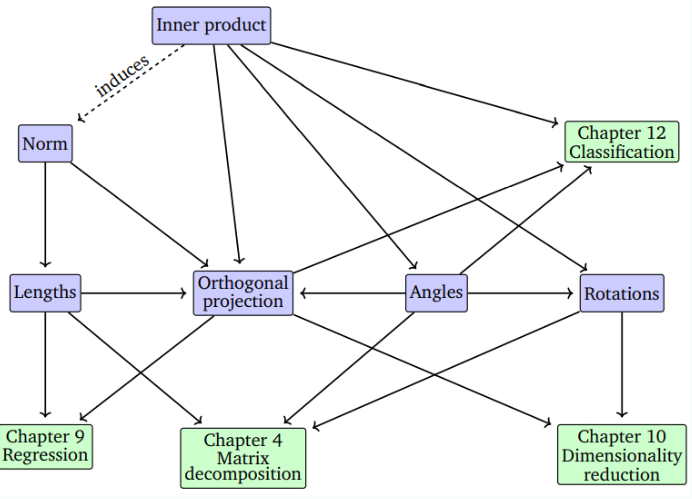
장에서는 이러한 개념들에 대한 기하학적 해석과 직관적인 이해에 대해 살펴봅니다. 특히 geometric vector를 살펴보고 두 벡터 간의 lengths, distances or angles 를 계산하는 방법도 살펴볼 것이다. 아래 그림은 장에서 배우는 개념들이 이후

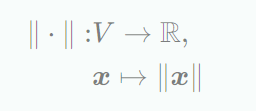
벡터공간 $V$에서 norm은 아래의 함수와 같다. 아래의 함수는 각 벡터 $x$를 그 벡터의 길이 $∥x∥∈R$로 매핑된다.또한 모든 $λ∈R$와 $x,y∈V$인 경우 아래 성질들이 성립한다.Manhattan norm은 다음과 같이 정의되며 $l_1$norm이라고도

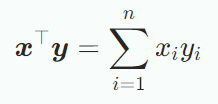
내적은 벡터의 길이나 두 벡터 간의 각도 또는 거리 등과 같은 직관적인 기하학적 개념을 도입하기 위한 것이다.내적의 한 타입인 scalar product/dot product는 다음과 같다.bilinear mapping $Ω$는 두 인자에 대한 mapping 이며, 각

내적을 통해 벡터의 길이를 계산할 수 있지만 모든 norm이 내적에 의해 유도되지는 않는다. (ex: Manhattan norm) 내적에 의해 유도되는 norm을 중심으로 lengths, distances, angles 같은 기하학적 개념을 살펴보자.Inner prod

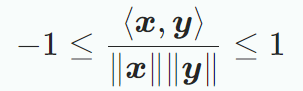
코시-슈바르츠 부등식을 사용하면 두 벡터 $x, y$가의 내적에서의 각도 $w$를 정의할 수 있다. x와 y가 0이 아닐 때, 다음과 같다.두 벡터간 유일한 각도 $w∈0,π$가 있을 때, 각도는 다음과 같다.두 벡터 간의 각도는 두 벡터의 방향이 얼마나 유사한지 알려

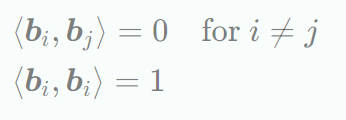
벡터공간 $V$와 기저 $b_1,...., b_n$가 있을 때, 다음이 성립할 때, 이 기저를 orthonormal basis라 한다.non-orthogonal이면서 unnormalized한 기저벡터 집합 $b_1,...., b_n$이 주어졌다고 할 때, 행렬 $B

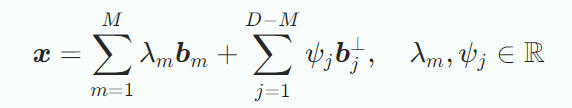
Orthogonality는 선형차원 축소에 쓰인다. D차원의 vector space V와 M차원의 subspace U에 대해 orthogonal complemnet $U^⊥$은 D-M차원의 subspace이며, U의 모든 벡터에 직교하는 V의 모든 벡터를 포함한다. $

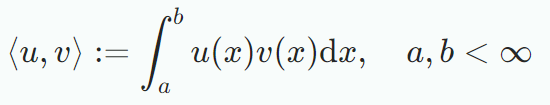
내적을 유한한 요소를 갖는 벡터에 대해서 다루던 기존과 달리 $x∈R^n$을 n개의 값을 가지는 함수로 생각할 수 있으며, 내적의 개념은 유한한 갯수의 요소를 갖는 벡터와 연속된 값의 함수로 일반화할 수 있다. 그러면 각 벡터요소들의 합은 적분으로 바뀐다.$u:R→R,

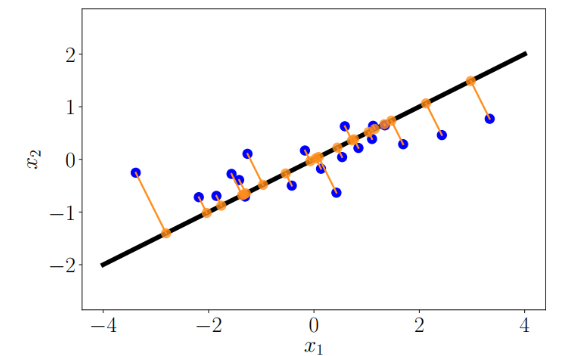
머신러닝에서 주로 다루는 고차원의 데이터는 시각화하거나 분석하기 어렵기 어렵다. 고차원 데이터는 대부분의 차원이 불필요한 요소로 되어 있기 때문에 데이터의 압축손실을 최소화하기 위해 가장 정보를 많이 담고 있는 차원을 찾는 것이 이상적이다. 주어진 저차원 subspac

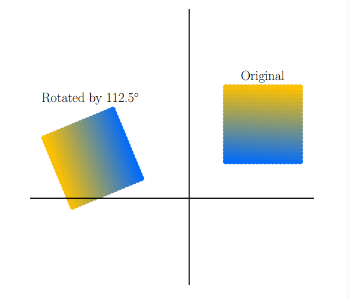
rotation은 원래의 평면을 $θ$만큼 회전시키는 것을 origin은 고정된 점이다. 일반적으로 회전은 반시계 방향을 기준으로 한다.위 그림은 반시계방향으로 $112.5^∘$ 회전시키는 것으로 이때 transformation matrix는 다음과 같다.$R^2$에서

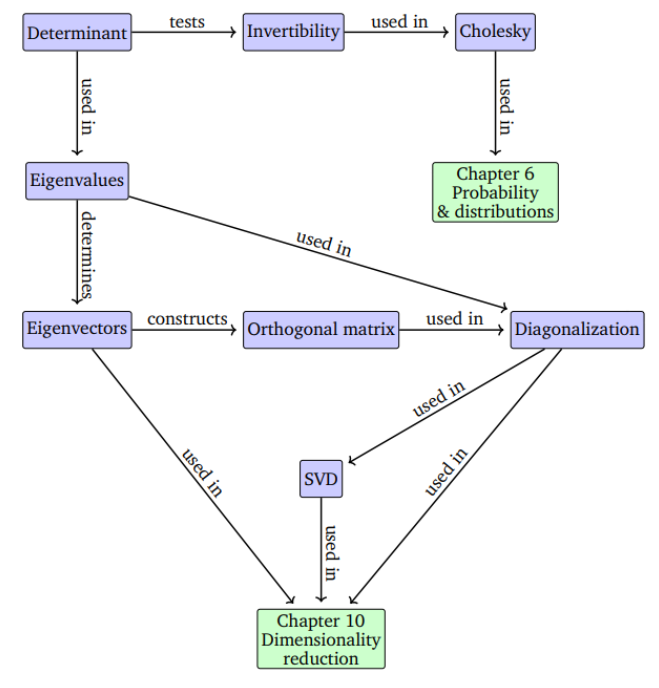
4장에서는 행렬의 전체 속성을 특성화하는 숫자로 행렬을 설명하는 방법에 대해 살펴본다. 4.1장의 Determinants와 4.2장의 Eigenvalues는 정사각 행렬인 경우에서 중요하다. 이러한 characteristic number는 중요한 수학적 결과를 가지고

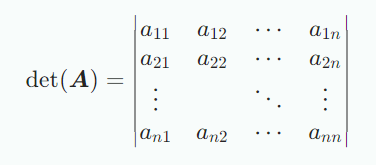
행렬식은 분석을 위한 수학적 도구이면서 선형연립방정식의 솔루션으로 매우 중요한 개념이다. 행렬식은 오직 정사각행렬에 대해서만 정의된다. 행렬식은 $det(A)$ 또는 $∣A∣$로 표현한다.행렬식은 정사각행렬을 실수로 매핑하는 함수로 볼 수 있다. 정사각행렬 $A$가 역