Ch2-8.Affine Spaces

Affine Subspaces

$V$가 벡터공간이고 $x_0 ∈ V$ 이고 $U⊆V$일 때, 다음과 같은 subset $L$은 $V$의 affine subspaces 또는 linear manifold라고 부르며 U 는 direction 또는 direction space 라고 하며, $x_0$은 support point라고 한다.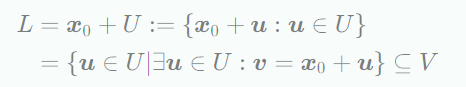

Affine subspaces는 보통 parameter 로 표현된다. k차원 $V$의 affine space $L=x_0+U$가 있을 때, $(b_1,...., b_n)$가 $U$의 기저일때, affine space x는 다음과 같이 표현될 수 있다. 다음과 같은 표현식을 $L$의 parametric equation 이라고 하며, $b_k$는 directional vectors이다.

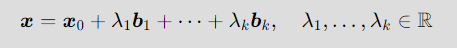
1차원 afffine spaces를 직선, 2차원을 평면, n-1차원에서는 hyperplanes라 부른다.

$A∈R^{m×n}, ,b∈R^m$일 때, $Ax = b$의 해는 공집합 또는 $n−rk(A)$차원의
$R^n$의 affinespace이다. 특히 $λ_1x_1 + ⋯ + λ_nx_n = b$의 해는 $R^n$에서의 hyperplane이다. $R^n$에서 모든 k-차원의 affine subspace는 inhomogeneous한 연립선형방정식 $Ax=b$ 의 해이다. 또한, Homogeneous 연립방정식 $Ax=0$ 의 해가 vector subspace라는 것을 떠올려보면, 이는 support point $x_0 가 0인 특별한 affine space라고 할 수 있다.

Affine Mappings

Linear mapping과 affine mapping은 많이 연관되어 있다.

Vector spaces $V,W$가 있고, linear mapping $Φ:V→W,a∈W$일 때, 다음의 mapping을 $V$에서 $W$로의 affine mapping이라고 한다. 여기서 $a$는 ϕ의 translation vector라고 한다.

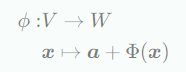
affine mapping은 다음의 성질을 가진다.

모든 affine mapping $ϕ:V→W$는 linear mapping $Φ:V→W$과 translation $τ:W→W$의 조합이다. 즉, $ϕ=τ∘Φ$이며 $Φ$ 와 $τ$는 유일하다.

afffine mapping의 조합 $ϕ’∘ϕ$도 affine이다.

Affine mapping은 기하학적 구조를 유지하며, dimension과 parallelism 또한 보존된다.