[BOJ 2616] 소형기관차 (Python)
풀이
처음 우선순위 큐와 방문 배열을 통해 최댓값을 구하는 방식으로 접근했다. 이는 잘못된 접근이었고 당연히 틀렸다. 이후로 계속 헤맸다...ㅠㅠ 점화식을 도출하여 DP를 사용해야겠다는 포인트는 잡았지만 점화식을 도출하지 못했다. 다른 사람들이 도출한 점화식의 풀이를 보면서 해당 문제를 풀 수 있었다.
DP[N][M] : 소형기관차 N대를 운행할 때 M번째 객차를 선택했을 경우의 최대 운송 손님 수 (기관차에 limit개의 객실을 넣을 때)
S[X] : X번째 객차까지의 모든 손님 수를 더한 배열
이 배열은 생성하는 이유는 X번째 객차를 선택했을 때 소형기관차가 끌 수 있는 손님 수를 바로 알 수 있기 대문이다.
--> S[X] - S[X - limit]
아래는 최종 점화식이다.
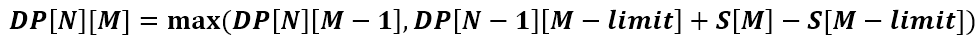
위 점화식을 이용해 2차원 리스트인 DP[N][M]을 채우면 된다. 아래 그림을 통해 이해해보자.
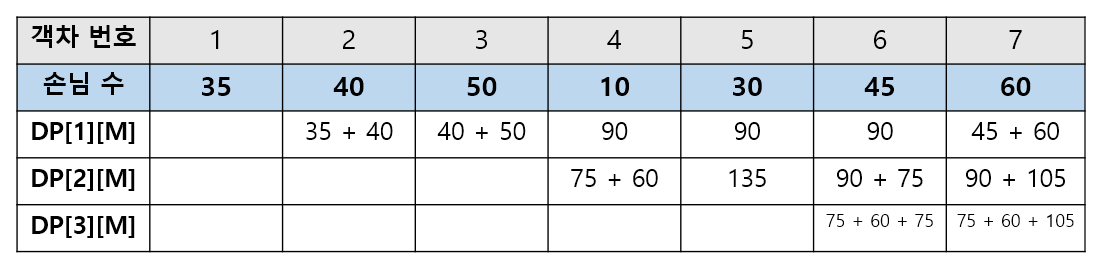
※ 이전의 값이 유지되면 합으로 표현하였고, 새롭게 갱신되면 '+'가 포함된 계산식으로 표현하였다.
몇 가지 경우를 살펴보자.
-
DP[1][2] = max(DP[1][1], DP[0][2-2] + S[2] - S[0]) 이다.
DP[1][1]은 0이고, DP[0][0]도 0이며 S[2] - S[0] 값만 계산하면 된다. S[2] - S[0]값은 1번 객차 손님 수 + 2번 객차 손님 수이다. 즉, 소형기관차 1대를 운행할 때 2번째 객차를 선택할 경우 최대 운송 손님 수는 75가 된다. -
DP[2][4] = max(DP[2][3], DP[1][4-2] + S[4] - S[2]) 이다.
DP[2][3]은 0이다. DP[1][2]는 75이며 S[4] - S[2]는 60으로 둘 중 큰 값인 135가 DP[2][4]의 값이 된다. -
DP[2][5] = max(DP[2][4], DP[1][5-2] + S[5] - S[3]) 이다.
DP[2][4]는 135이다. DP[1][3]은 90이고 S[5] - S[3]은 40이다. 135와 130중 큰 값은 135이므로 DP[2][5]는 135가 된다.
즉,현재 운행하고 있는 소형기관차가 전의 객차를 유지했을 때와두 번째 객차를 선택하기 전으로 돌아가 첫 번째 소형기관차의 객차 + 두 번째 소형기관차가 M번째 객차를 선택했을 때의 2가지 경우 중 최대로 손님을 운송할 수 있는 경우를 선택하는 것이다.
최종적으로 점화식이 의미하는 것은 현재 운행하고 있는 소형기관차가 전의 객차를 변경없이 유지했을 때 (DP[N][M-1])와 N번째 소형기관차가 객차를 선택하기 직전으로 돌아가 N-1번째 소형기관차의 객차를 유지하면서 (DP[N-1][M-limit]) N번째 소형기관차가 M번째 객차를 선택했을 때 (S[M] - S[M-limit])의 2가지 경우 중 최대로 손님을 운송할 수 있는 경우를 선택한다는 것이다.
코드
import sys
input = sys.stdin.readline
N = int(input())
train = list(map(int, input().split()))
limit = int(input())
# 구간합 계산
S = [0]
value = 0
for t in train:
value += t
S.append(value)
dp = [[0] * (N + 1) for _ in range(4)]
# 점화식을 이용해 최댓값 탐색
for n in range(1, 4):
for m in range(n * limit, N + 1):
# n = 1일 때 선택한 객차가 없으므로
# 전에 계산한 구간합과 현재 계산하는 구간합 중 최댓값을 계산해 갱신해준다.
if n == 1:
dp[n][m] = max(dp[n][m - 1], S[m] - S[m - limit])
# 점화식
else:
dp[n][m] = max(dp[n][m - 1], dp[n - 1][m - limit] + S[m] - S[m - limit])
# print_dp(dp)
print(dp[3][N])참고 : https://kjwsx23.tistory.com/398
https://lyzqm.blogspot.com/2017/03/2616.html