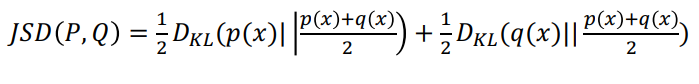2020 데이터 청년 캠퍼스(경기대)에서 학습한 내용을 간단하게 요약하였습니다.
2020.07.06 ~ 2020.07.10
Probability Theory
- 어떤 현상 발생에 대한 불확실성을 정확하고 정량적으로 표현 가능한 수학적 프레임워크 제시 (확률적으로, 수학적으로 제시)
- 고등학교 수학 과목의 확률이라 생각하면 될 것 같다.
- 어떤 현상이 불확실하게 일어나기 때문에 확률로 표현해야함!
확률의 공리
- 0과 1 사이의 숫자로 표현

Frequentist probability
- 확률 변하지 않음
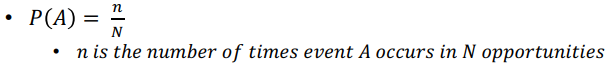
- N : 모든 사건들 (all events)
- n : 특정 사건이 일어날 빈도 수
Bayesian probability
- 확률 변함
- 믿음의 정도(가설이 타당할 정도)를 표현

- 데이터가 이미 존재하고 불완전한 지식이 있을 때, 이 지식을 사용하면 확률을 얻을 수 있다는 것
Probability distribution
-
이산형 (Discrete)
- 정수와 같이 명확한 값을 변수값으로 함
- 확률변수가 가질 수 있는 값의 수가 한정되어 -> 그 수를 셀 수 있는 변수
- (ex) 주사위를 굴려서 나오는 수의 확률 -> 1/6, 1/6, 1/6, 1/6, 1/6, 1/6
-
연속형 (Continuous)
- 변수값이 정수처럼 명확하지 못함
- 확률변수가 연속량으로 표기되어 가능한 변수값의 개수를 셀 수 없음
- (ex) C언어 과목을 수강하는 학생들의 평균 몸무게
이산형 (Discrete)
- 확률 질량 함수 (Probability mass function - PMF)
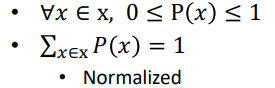
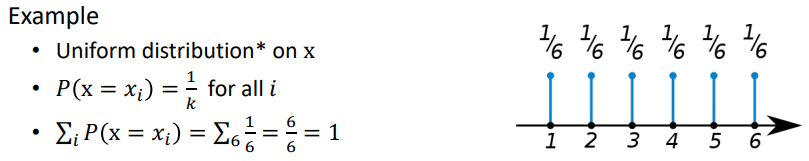
- 셀 수 있으며, 모든 확률변수의 합이 1이다.
연속형(Continuous)
- 확률 밀도 함수 (Probability density function - PDF)
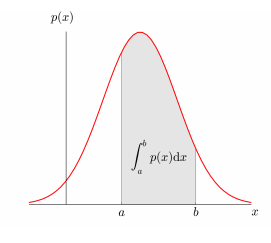
- 연속적인 값들 사이에 확률변수값이 분포되어 있다. 위와 같은 분포도를 가지게 된다.
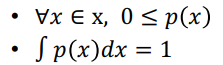
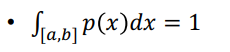
- a ~ b인 특정 범위에 확률변수의 합이 1이다.
결합 확률 분포 (Joint probability distribution)
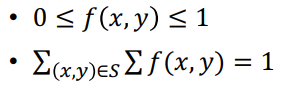
(ex)
- x는 학생이 가진 공책의 개수, y는 펜의 개수
- 학생이 가진 소지품에 대한 joint probability는 f(x,y)
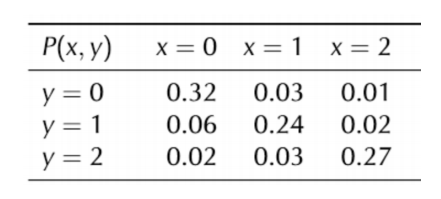
이러한 확률을 가지게 된다.
조건부 확률 (Conditional probability)
- 다른 사건이 발생한 경우를 고려했을 때, 어떤 사건의 확률
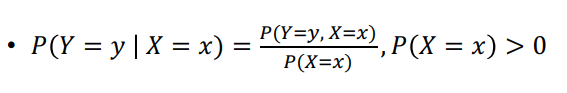
Bayes' rule (베이즈 룰)
- 이전의 경험(과거의 data)과 현재의 증거(현상)를 토대로 어떤 사건의 확률을 추론하는 과정을 서술

사전 확률-> 사후 확률 (오타 났음)- (ex) 여기를 참고하자.
Chain rule
-
2개 이상의 함수를 하나의 함수로 결합하여 만들어진 함수
-
<공식을 도출하는 과정>
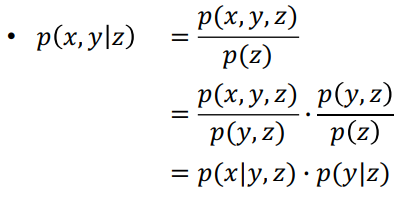
-
<공식>
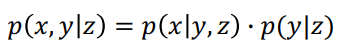
-
(ex)
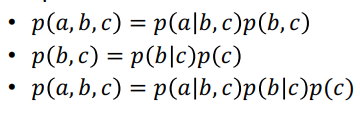
독립 & 조건부 독립
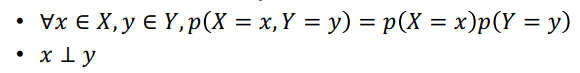
- (ex) 랜덤변수 X, Y, Z가 주어졌을 때
X, Y가 독립이 아닐 때(교집합이 존재), Z가 생성될 경우 X와 Y가 독립!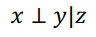
기댓값과 분산 (Expectation & Variance)
-
이산형 기댓값
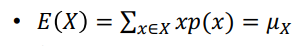
-
연속형 기댓값
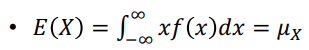
-
분산
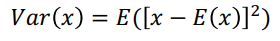
Var(X) = E(X^2) - {E(X)}^2
sqrt(Var(X))는 표준편차!
Maximum likelihood (ML)
- Likelihood : 관측된 데이터(y)과 나올 확률
-> 최대의 확률을 찾고자 하는 것 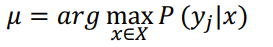
- (ex) 고객 만족이 최대인 제품을 찾아보자.
x : 제품의 특성
y1 : 좋아요
y2 : 싫어요
구하고자 하는 궁극적인 목표값은 argmax P(y1|x)이다.
argmax P(y1|x) = 좋아요를 누를 확률인 가장 큰 제품을 select 해준다.
Information Theory
- 기계 학습(Machine Learning) 모델이 믿을만 한지를 측정하는 이론
- Information이라는 개념을 수학적으로 표현
- 잘 일어나지 않는 사건(unlikely event)의 정보는 자주 발생할 만한 사건보다 정보량이 많다고 할 수 있음.
Bit flip
- 동일한 메모리 row에 반복적 접근 과정을 통해 방해가 발생하면서 메모리가 온전히 전달되지 않는 현상
Entropy
- 어떤 사건이 정보적 측면에서 얼마나 중요한가를 반영한 로그지표에 대한 기댓값
- 특징 추출(Feature Extraction) 하는데에 사용
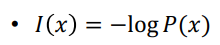
- 사건에 대한 정보를 X = x라 한다.
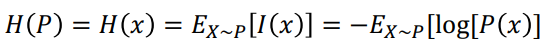
- 사건이 무엇인지 정의
- 각 사건의 확률 계산
- Entropy 계산
- 데이터셋의 변수(특징)가 엄청 많은 경우
변수들의 집합의 모든 경우의 수를 찾고 -> 그 경우의 수들의 Entropy값들 중, 가장 작은 Entropy 값인 집합의 경우를 Feature로 추출 -> 모델링 -> 성능 향상!
Kullback-Leibler(KL) divergence(발산)
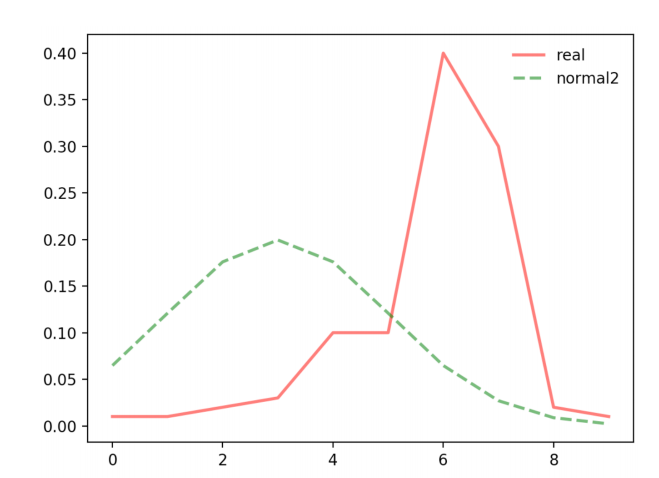
-
두 확률분포의 차이를 계산하는데 사용하는 함수
-
정보 엔트로피의 차이를 계산하는데 사용하는 함수
-
이산형
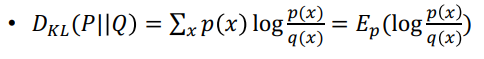
-
연속형
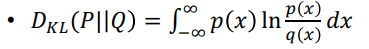
-
Dkl (P||Q) >= 0 이다.
-
비대칭성 이다. -> 거리개념이 아니다.
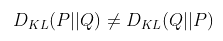
-
KL Divergence의 값이 작을수록 두 확률분포는 유사함
Jensen-Shannon divergence
- 두 확률분포간의 유사성을 측정하는 방법
- KL divergence를 기반으로 함
- 대칭성 이다. (KL divergence를 대칭성으로 만들어줌) -> 거리개념으로 가능
- 항상 유한한 값을 가진다.