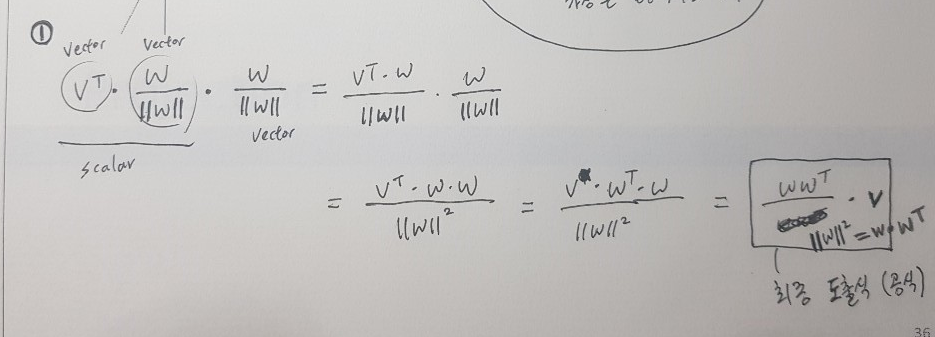2020 데이터 청년 캠퍼스(경기대)에서 학습한 내용을 간단하게 요약하였습니다.
2020.07.06 ~ 2020.07.10
선형대수 (Linear Algebra)
- Linear equations(Ax=b)로 표현 가능한 system을 푸는 방법론
- 선형성(linearity)을 가지는 대수(algebra)로 이루어진 방정식의 해를 구하는 방법론
스칼라 (Scalars)
- 하나의 숫자
- 크기만 있고
방향을 가지지 않음 - italic체, 소문자로 써야함
벡터 (Vectors)
- 숫자들의 배열
- 순서대로 정렬됨
- 왼쪽의 x는 소문자로 굵게 써야함
- 요소들은 italic체, 소문자, 번호 붙여야함 (x1, x2...)
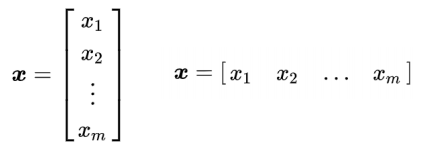
행렬 (Matrices)
- 2차원 배열의 숫자로 각 요소를 2개의 인덱스로 구분
- 변수이름 대문자로 굴게 써야함
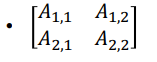
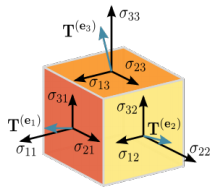
텐서 (Tensor)
- 3차원 이상의 배열 (4차, 5차...)
Matrix Product
- 우리가 아는 일반적인 행렬의 곱셈
- A * B = C
- (mn)행렬 (np)행렬 = C는 (mp)행렬이 됨
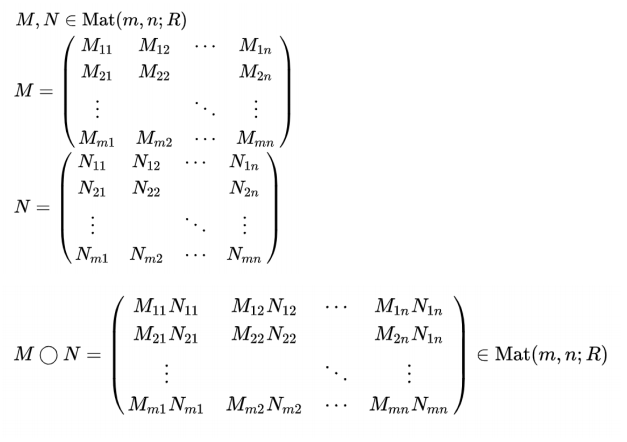
Hadamard Product
- 1행 1열끼리 곱하고, 1행 2열끼리, 1행 3열끼리... 곱하는 방식
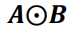
Dot Product
- 행렬의 차원을 변환
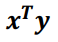
- 열벡터 -> 행벡터로 변환
Properties
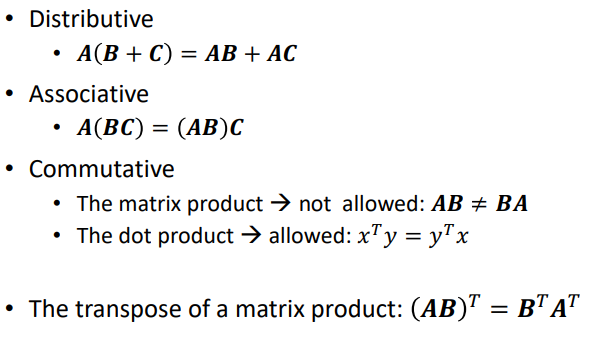
선형 방정식 (Linear Equations)
A * x = b
- A : Data
- x : weight (가중치)
- b : Loss or Accuracy
- Loss가 최소, Accuracy가 좋은 경우의 모델링을 찾는 것이 궁극적인 목표!
단위 행렬 (Identity Matrix)
- A * I = A
- B * I = B
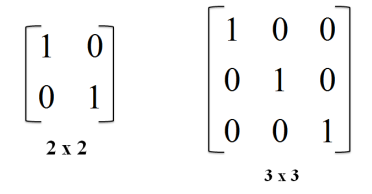
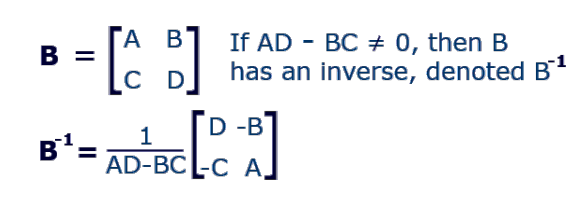
역행렬 (Matrix Inversion)
- A * ★ = I
- A와 ★를 곱했을 때 단위행렬이 나올 때, ★의 행렬식
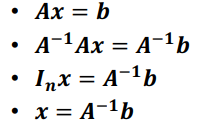
Linear Independence
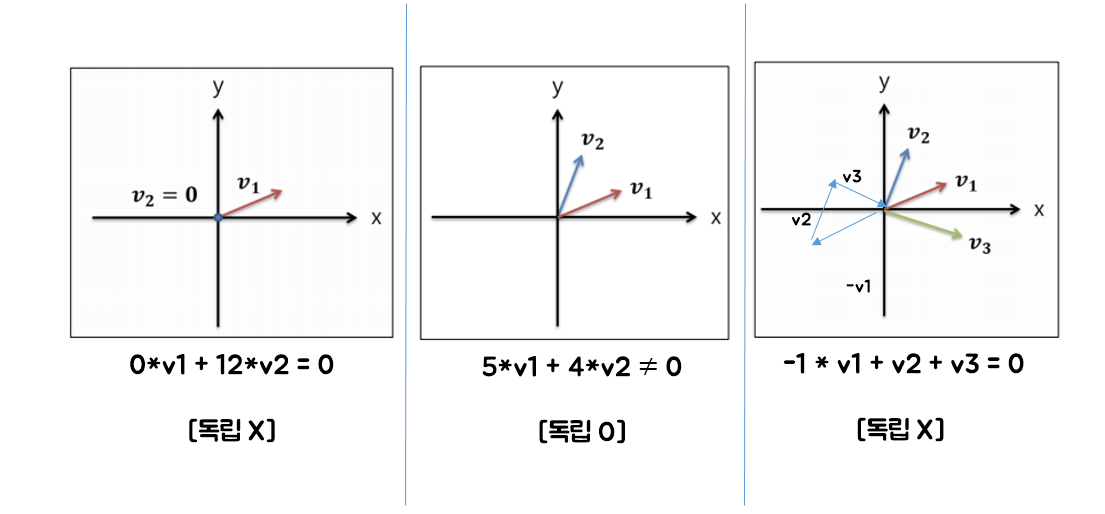
- vector가 독립적인지 아닌지 판단
- vector가 독립일 때
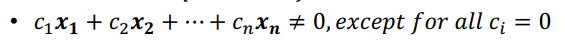
- vector가 독립 X
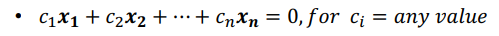
- (ex)
Basis
- 어떤 벡터 공간의 기저(basis)는 그 벡터 공간을 선형 생성하는 선형독립인 벡터들이다.
- 즉 벡터 공간의 임의의 벡터에게 선형결합으로서 유일한 표현을 부여하는 벡터
- 여기를 참고해보자
차원 (Dimension)
- 기저 벡터의 갯수를 차원이라 부른다.
- 쉽게 말해 3차원 공간을 구성하는데에는 3개의 기저벡터가 필요
- 여기를 참고해보자
랭크 (Rank)
- 어떤 행렬A의 랭크는 해당 행렬의 열벡터에 의해 span된 벡터공간의 차원이라 하자.
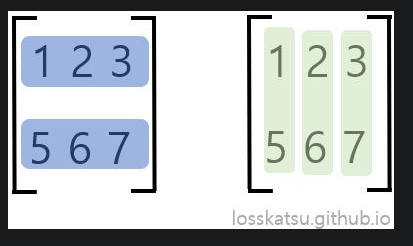
- 위 행렬의 랭크는 2이다.
- (6x5)의 행렬 데이터를 (6xk), (kx5)로 나눠 다른 관점에서 데이터를 보게 한다.
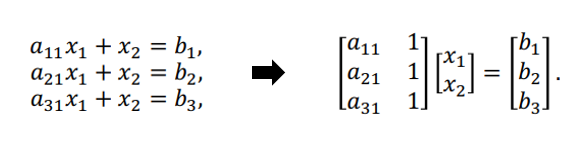
행렬의 선형 방정식 (Linear Equations as Matrix)
- 행렬로 표현하기 위해 다음 3가지 필요
- 계수 행렬 = A
- 미지수 벡터 = x
- 우변 벡터 = b
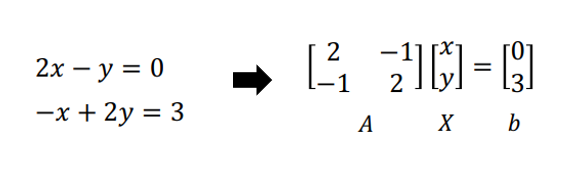
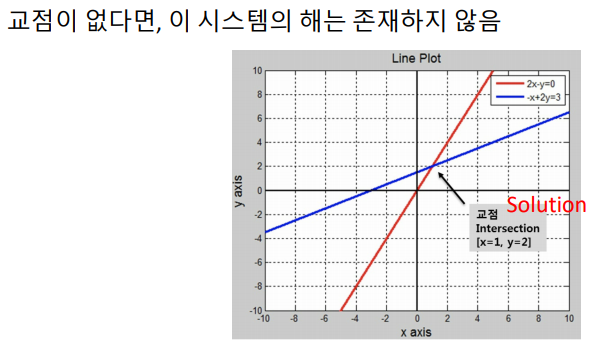
- Row picture (행 중심)
- 각 row에 해당하는 방정식을 한 번에 하나씩 보는 것
- 교점이 시스템의 해
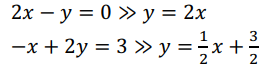
- Column picture (열 중심)
- 행렬에서 column 방향으로 확인
- 계수 행렬의 각 column이 공간상에서 벡터로 표현
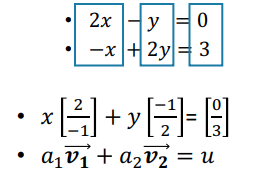
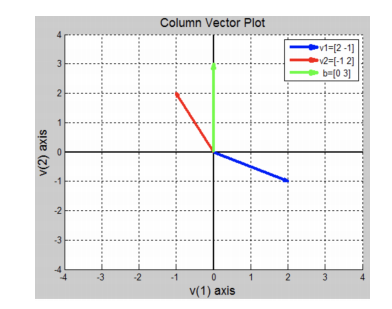
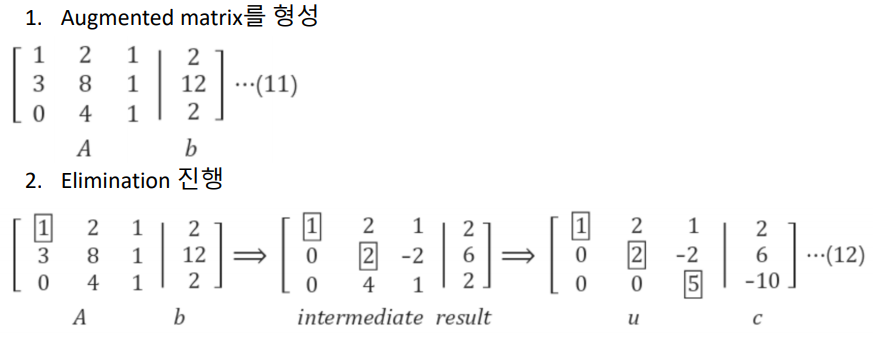
소거법 (Elimination)
- 어떤 시스템의 해를 구하기 위한 방법 -> Upper triangular matrix or Lower triangular matrix로 만들기 위한 과정
- 3개의 선형 방정식을 system matrix로 표현
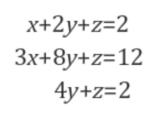

- A만 사용!!
- 기준이 되는 Pivot에 상수를 곱하고, 제거하고자 하는 식에서 소거 진행
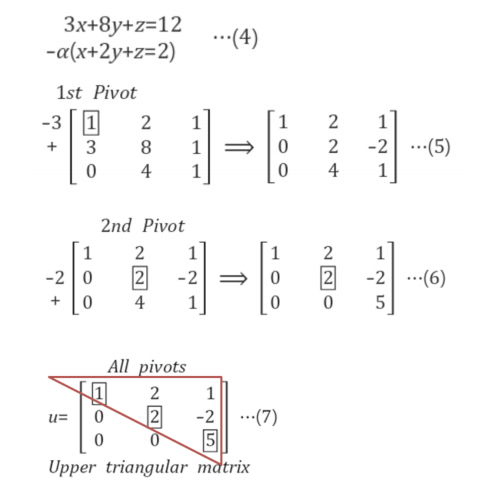
후방 대입법 (Back Substitution)
- A,b를 동시에 이용하여 시스템의 해를 구하는 과정

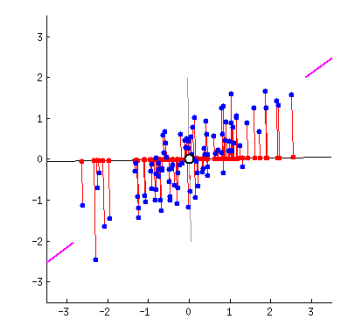
Orthogonal Projections
- 고차원 Data를 저차원의 Data로 변환하는 것
- PCA : 데이터의 분산을 최대한 보존하면서 서로 직교하는 새 축을 찾아 고차원의 공간들의 표본을 연관성이 없는 저차원 공간으로 변환하는 기법
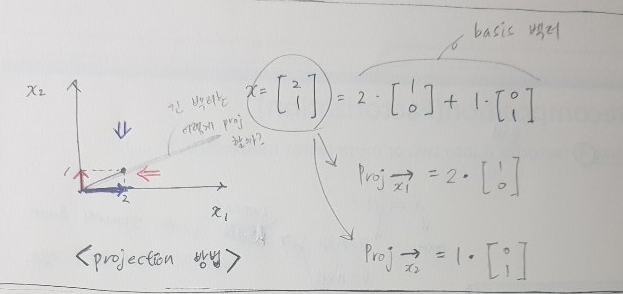
선에 투영 (Project onto a Line)
- 방향, 크기 를 고려해라
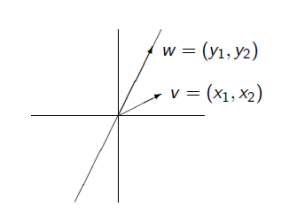
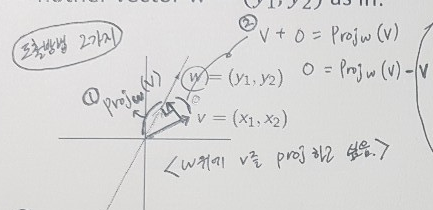
- (ex)
행렬 분해 (Matrix Decomposition)
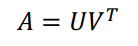
- A : (mxn) 행렬
- U : (mxk) 행렬
- V : (nxk) 행렬
- k의 차수가 Latent vector space의 Rank이다. (잠재적 벡터 공간의 랭크)
행렬식 (Determinant)
- 특별한 정의가 없음
- 결정자의 결과값은 그 행렬의 특성을 결정짓는 중요한 값이여서 Determinant라 불림
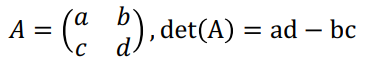
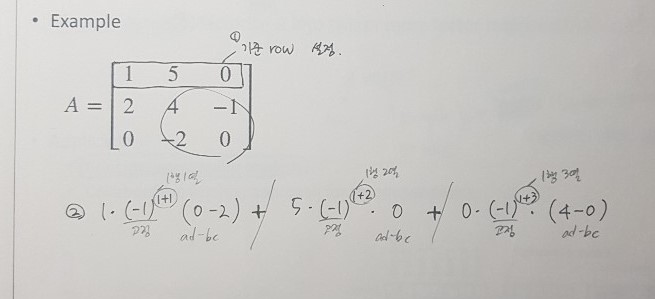
- (nxn) 행렬의 n>=3인 경우
고유값과 고유벡터 (EigenValues & EigenVectors)
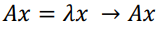
- 고유벡터 (EigenVectors) : 선형변환 A에 의한 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터 (x)
- 고유값 (EigenValues) : 상수배값
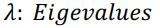
- Vector x는 행렬 A에 의해 원래와 다른 방향으로 변환됨
- Ax가 x와 평행한 경우가 존재

- 고유값 분해 (EigenDecomposition)
- 정방행렬에 대해서만 가능, 그 중에서도 일부 행렬에 대해서만 적용 가능한 대각화 방법
(ex)
1. EigenValues 구하기

2. EigenVectors 구하기
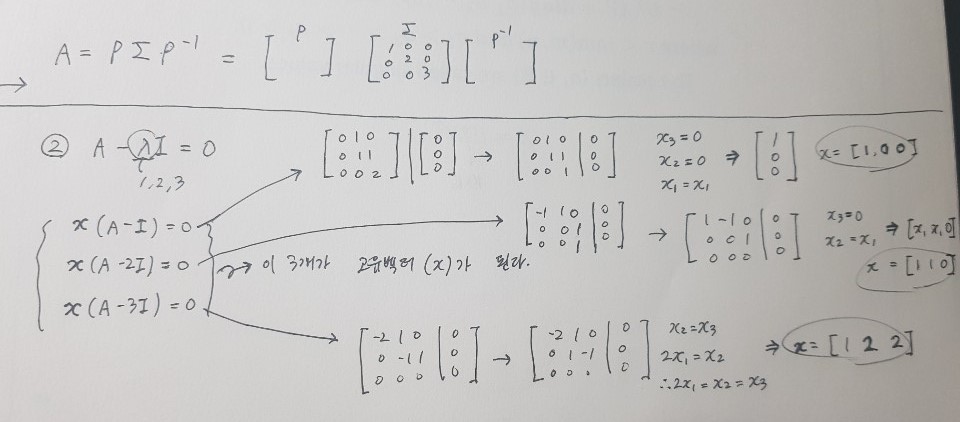
특이값 분해 (Singular Value Decomposition)
- SVD
- 고유값 분해(EigenDecomposition)처럼 행렬을 대각화하는 하나의 방법
- 특이값 분해가 유용한 이유? -> 행렬이 정방행렬이든 아니든 관계없이 모든 (mxn)행렬에 대해 적용이 가능하기 때문!
- 데이터에서 특징을 뽑아내는 성능이 좋은 방법 중 하나

- 여기를 참고하자.
주성분 분석 (Principal Component Analysis)
-
PCA
-
사실 선형대수학이라기 보다는 선형대수학의 활용적인 측면이 강함
-
영상인식, 통계 데이터 분석(주성분 찾기), 데이터 압축(차원 감소), 노이즈 제거 등에 활용
-
대표적인 차원 축소 알고리즘
-
데이터에 가장 가까운 초평면을 구한 후 -> 데이터를 이 초평면에 투영(projection) 시킴
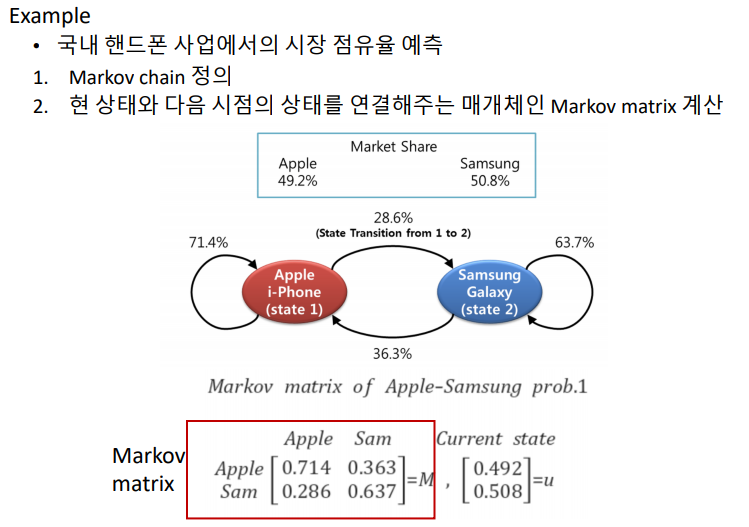
Markov Matrix
-
Markov Chain을 기술하기 위한 수학적 도구 / Markov Chain을 연결시켜주는 매개체 역할
Markov Chain
- 확률을 이용하여 어떤 객체 상태를 시간에 따라 어떻게 변화할지(update)를 모델링 하는 것
- chain이라는 단어가 의미하듯이 객체의 시간에 따른 서로 다른 상태를 어떻게 연결할 것인지를 기술하는 것(ex) 날씨 예측, 인구 이동 예측 등과 같이 객체(날씨, 인구)의 상태(맑음, 흐림, 10만명, 5만명, ...)가 시간이 지남에 따라 어떻게 변화할지를 확률을 이용하여 예측하는 것
-
확률적 방법을 기반으로 함
-
-
- Markov chain state transition diagram을 정의
- Markov Matrix를 생성 (1번을 이용해서)
- 상태에 대한 probability를 계산
-
u * M을 하면 다음 state에 대한 정보를 계산할 수 있다.