2020 데이터 청년 캠퍼스(경기대)에서 학습한 내용을 간단하게 요약하였습니다.
2020.07.06 ~ 2020.07.10
Optimization
- 특정 제약조건을 만족시키면서 함수 f의 값을 최소화하는 변수 x의 값 x* 발견
- 최대화 문제의 경우 : f(x) -> - f(x)
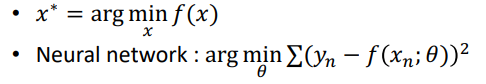
- 기계학습에서 Task를 f(x)로 놓는다면, Training은 찾아가는 과정이며 x는 parameter이다.
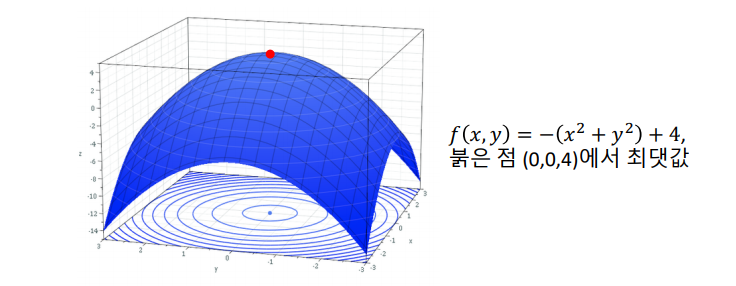
빨간점이 도착점이다.
- 최적화 원리
-
-
초기화
-
반복적인 갱신 (Optimizer가 하는 역할)
- 방향(기울기 -> 미분)을 어떻게 결정하는가
-
종료
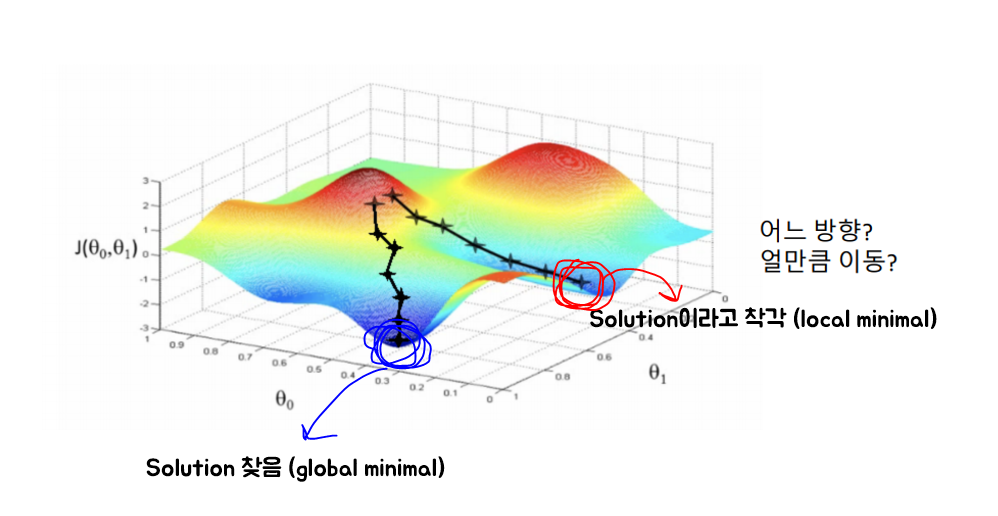
- solution을 찾아서 종료
- solution을 찾았다고 착각해서 종료
- parameter에 의해 강제 종료
-
-
목적 함수 (Objective Function)

- Target : 도착해야하는 목표
- f(x) : 결과값 (모델링 예측한 값)
- Target - f(x) 사이의 Loss 계산
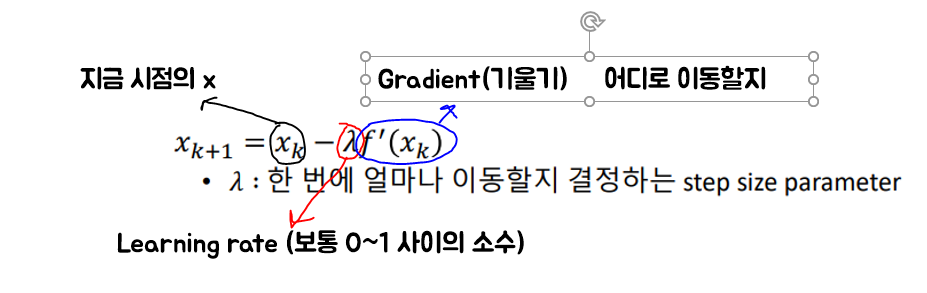
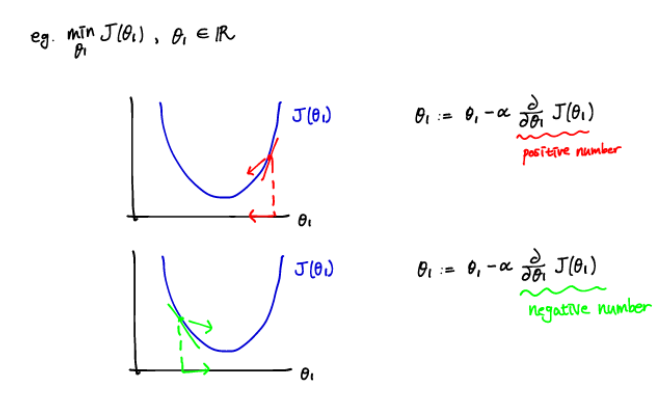
- 1차 미분
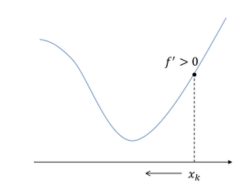
람다가 양수
f'(xk)가 양수여서 xk가 왼쪽으로 감
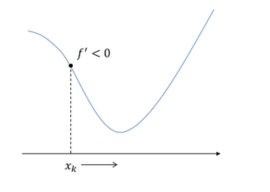
람다가 양수
f'(xk)가 음수여서 xk가 오른쪽으로 감
- 극소점에 갈수록 학습속도가 너무 느려지는 문제 발생 (-)
- 2차 미분

- 변곡점 ( f''(x)=0 근처에서 매우 불안정) (-)
- 이동할 방향이 정해져 있지 않음 (-)
-- 정리
| 1차 미분 | 2차 미분 | |
|---|---|---|
| 장점(+) | 방향 잘 감 | 1차보다 빠르다 |
| 단점(-) | 극소점 가면 느려짐 / 람다 정하는게 어려움 | 변곡점에 어려움이 많음 |
Convex Problem
- 문제를 풀기 좀 더 쉽게 만들어줌
- 학습속도가 느려도 어찌됐든 Gradient = 0인 최소값에 도달만 할 수 있도록 바꿔주는 것
[그림]
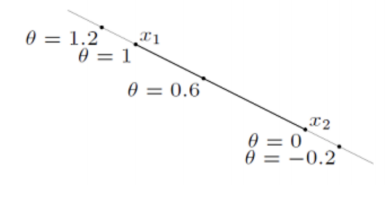
- Line
- 두 점을 지나며 양쪽 방향으로 무한히 커지는 직선
- R에 있기만 하면 됨
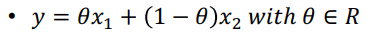
- Line segment
- 두 점 사이에서 정의되는 직선
- 끝과 끝이 세타범위에 존재해야 함
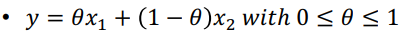
- Ray
- 한 점에서 시작해 다른 점을 지나며 무한히 커지는 선
- 세타가 >= 0 이여야함
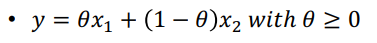
Affine set
- 점, 직선, 평면 등과 같이 선형적 특성이 있으면서
경계가 없는 집합 - Affine combination
- 여러점이 linear combination할 때 계수의 합이 1인 경우
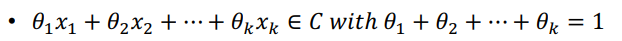
Convex Set
- 특정 set내의 x1과 x2를 잇는 선분(line segment)
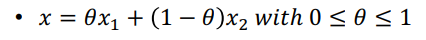
- Set이 존재하고, x1과 x2를 잇는 선분이 set에 포함되는 경우
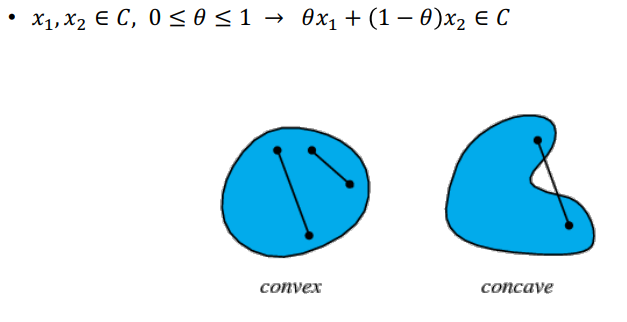
Cone
- 무한히 진행되며 나머지 방향에서는 정의되지 않는 집합
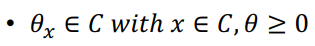
Convex cone
- cone이면서 convex인 경우를 의미
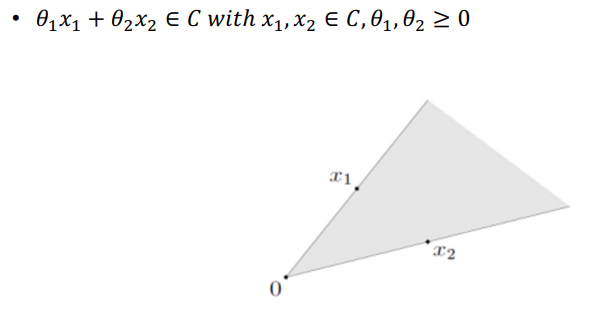
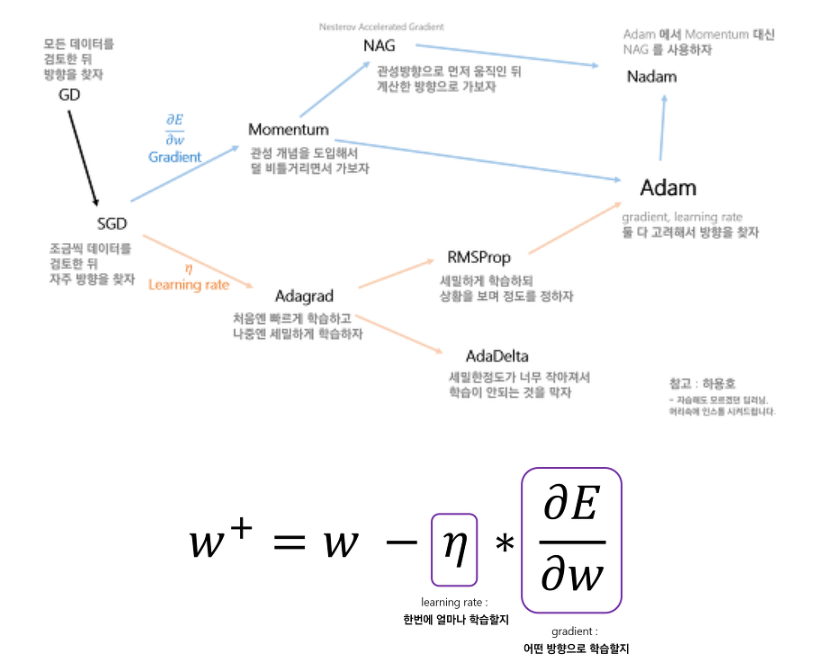
Optimizer
- ★ "왜 이 Optimizer를 썼어요"라는 질문에 답변할 수 있어야함.
-> 항상 근거가 필요 -> Why~? - 목적 :

- Gradient Descent (경사 하강법)
- 미분가능한 convex function의 optimum point를 찾는 방법 중 하나
- 최소 탐색 문제는 Gradient의 역방향 -> 전체 함수의 값 감소
- 최대 탐색 문제는 Gradient의 정방향 -> 전체 함수의 값 증가
- 현재 위치(높이)에서 가장 가파른 기울기를 가지는 쪽으로 가면 빨리 내려갈 수 있다는 아이디어에를 기반
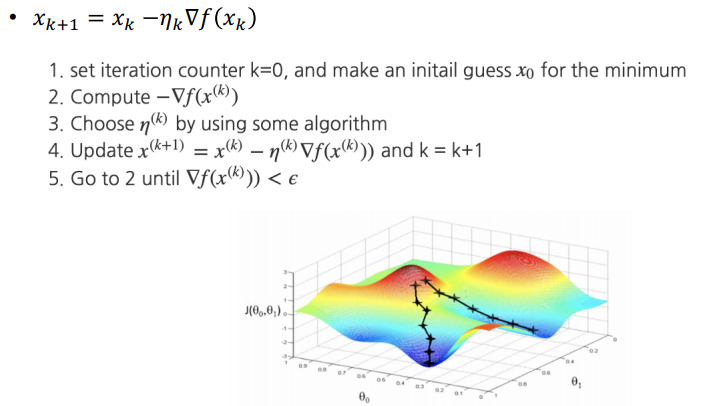
- Stochastic Gradient Descent (SGD)
- 데이터의 양이 많으면 최적해를 찾아가는데 오래 걸림
- 잘게 잘라서 돌리자 (mini-batch)

-
장점 단점 핸들링 쉬움 지역최적해에 빠질 가능성이 높음 (잘게 잘린 데이터안에 전역최적해 없으면 망한다 -> 느려짐) Gradient만 필요 초기화, parameter 튜닝 어려움 효율성 좋음
- Momentum
- Gradient descent를 통해 해를 찾는 과정에 일종의 '관성' 부여
- 지역최적해에 빠졌을 때, 나올 힘(관성)을 주는 것
- 현재 Gradient로 이동하는 것과 별개로 과거의 이동방향을 이용

-
장점 단점 SGD에서 지역최적해에 빠졌을 때 나올 힘을 주게 되어 탈출할 수 있게 됨 정해야할 parameter가 2배이므로, 각 parameter에 저장해야할 양도 2배 -> 필요한 메모리 2배 관성을 멈출 수 없는 경우가 생김
- Nesterov Accelerated Gradient (NAG)
- 현재 위치에서의 Gradient와 momentum step을 독립적으로 계산 후 취함
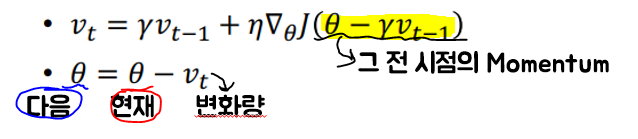
- Momentum vs NAG
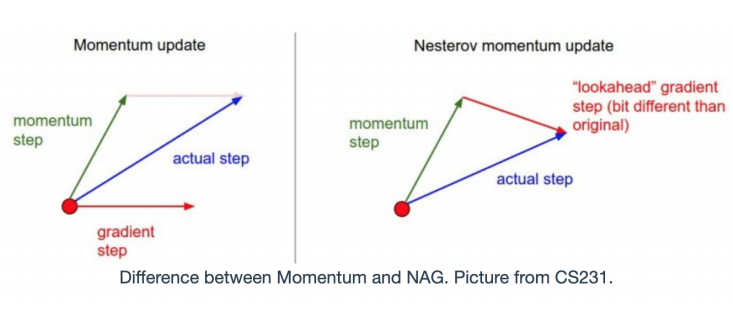
- 실제 갈 step 계산 시 momentum step이 영향을 끼침
-> 멈춰야 할 시점에 멈추지 못할 경우가 생김
- Adaptive Gradient (Adagrad)
- 변수 update시점 마다 step size를 다르게 설정
- 지금까지 많이 변화하지 않은 변수들은 step size를 크게
- 지금까지 많이 변화한 변수들은 step size를 작게

-
장점 단점 Learning rate을 수동으로 조정할 필요가 없음 (default=0.01로 시작) 분모에 제곱된 기울기를 축적(당연히 Lr이 엄청 작아짐) -> Update되는 값이 점점 작아짐 -> 결국 움직이지 않는 상황 발생
- RMSProp

- vs Adagrad
- 제곱된 Gradient의 값을 그대로 가져오는 대신에 r(비율)을 통해 재귀적으로 정의
- Gradient 변화량의 변수간 상대적 크기 차이를 유지 가능
- Adadelta
- Learning rate의 분모가 너무 커져서 Learning rate이 엄청 작아지는 현상을 막기 위한 방법

- Adam
- Optimizer로 제일 많이 쓰임
- RMSProp + Momentum

Summary