KMP(Knuth-Morris-Pratt) Algorithm
1. 부분 일치 테이블(pi[]) 구하기
pi[]는 부분 일치 테이블입니다.- 부분 일치 테이블이란, 현재 위치(~i)까지의 문자열 중,
접두사와 접미사가 일치하는 문자열의 최대 길이를 담고 있는 배열입니다.
1.1 pi[]가 무엇인지 gif로 이해해봅시다.
추가 설명
pi[i]의 결과값(N)이 가지고 있는 정보는
현재 위치(=i)까지의 문자열 중 길이가 동일하게 N인 접두사와 접미사는 서로 일치한다입니다.- 예를 들어서, 다음과 같이 현재 인덱스가
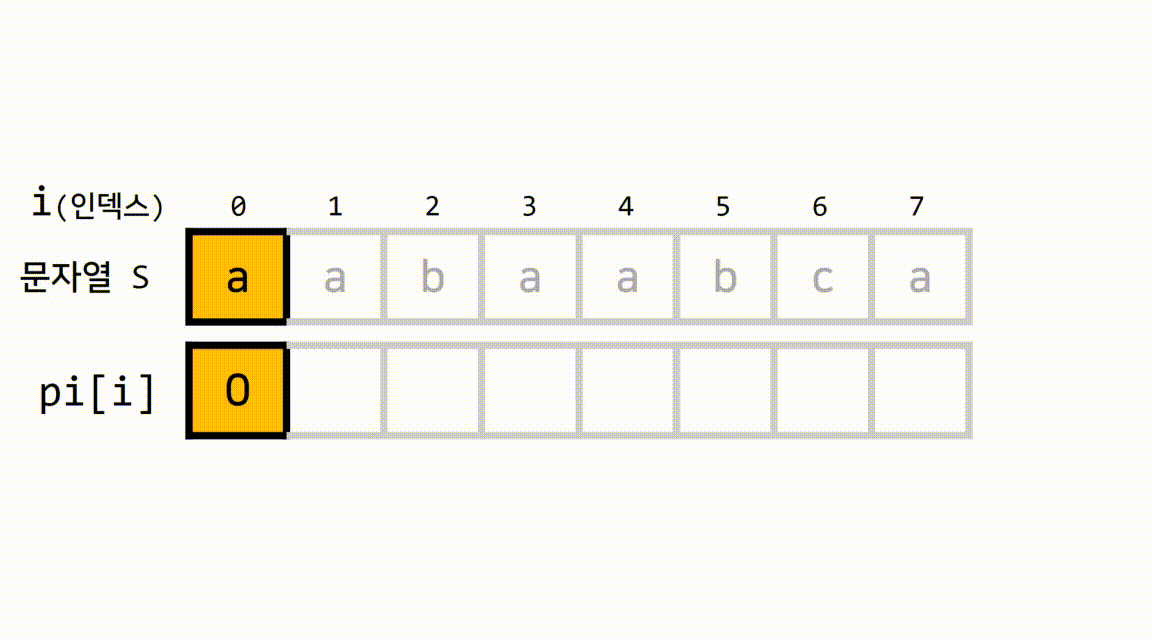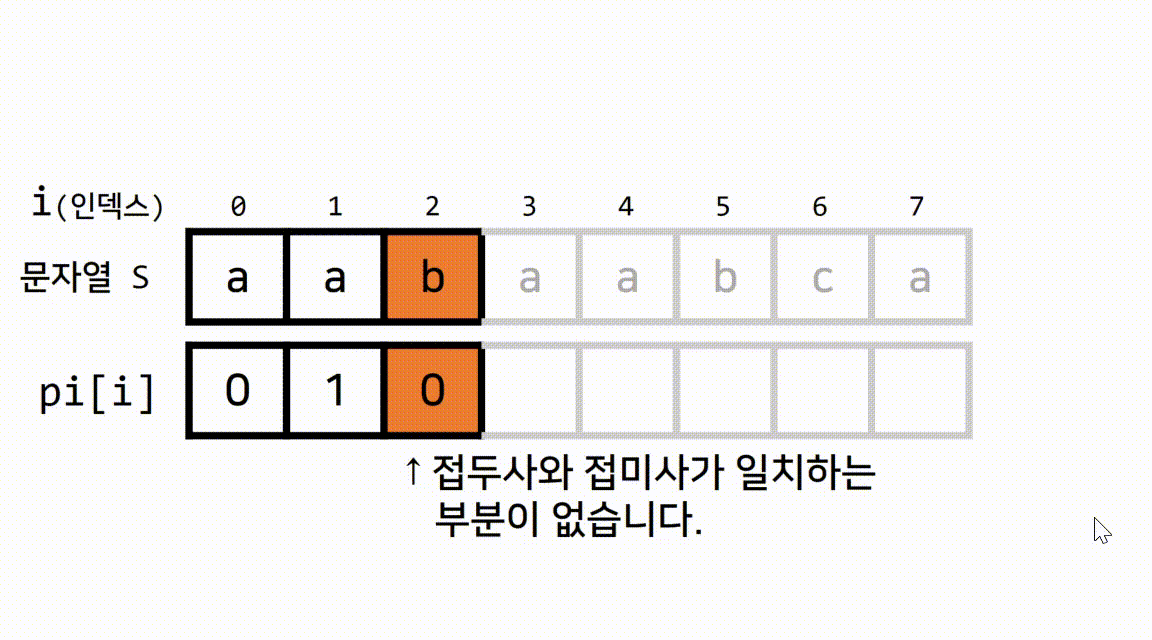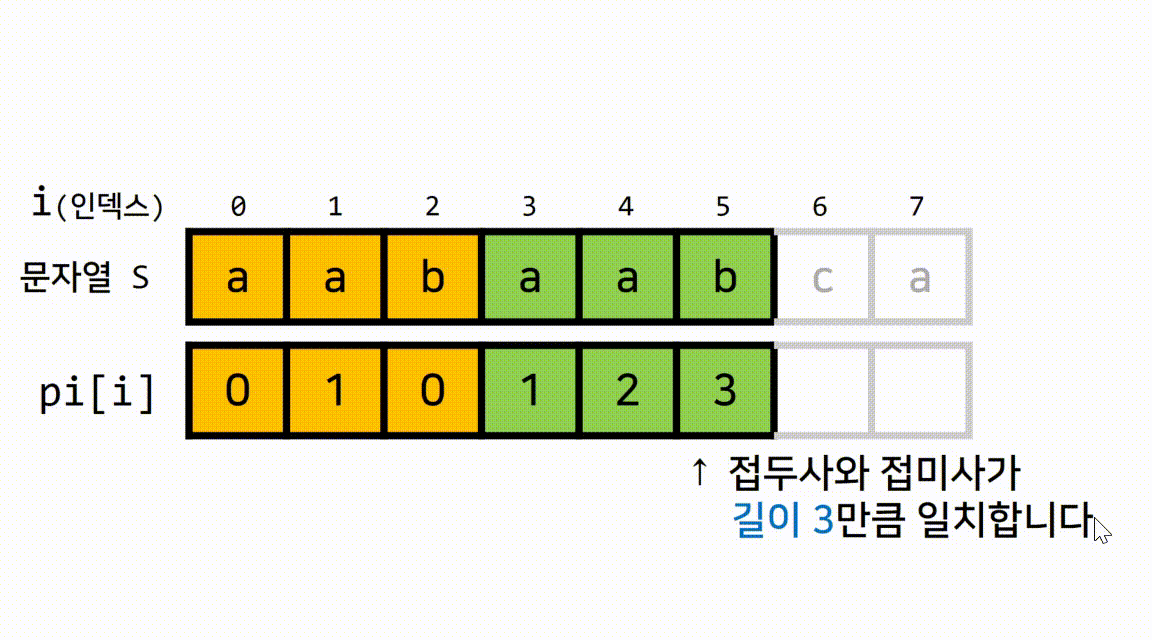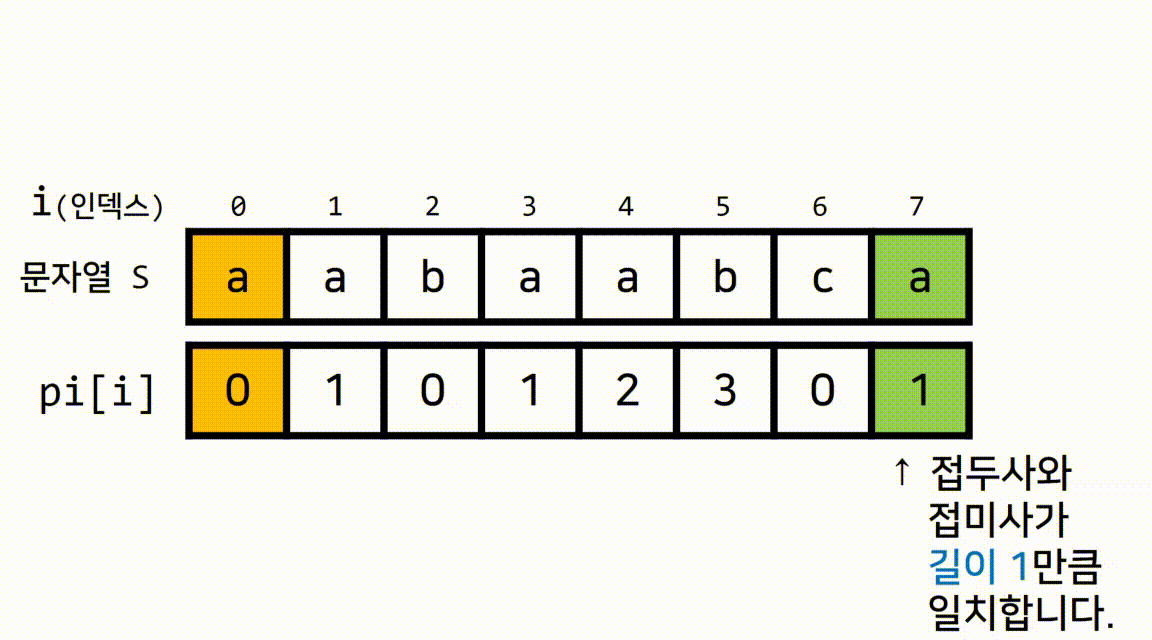
i=5일 때pi[5] = 3를 보고 알 수 있는 정보는 무엇일까요?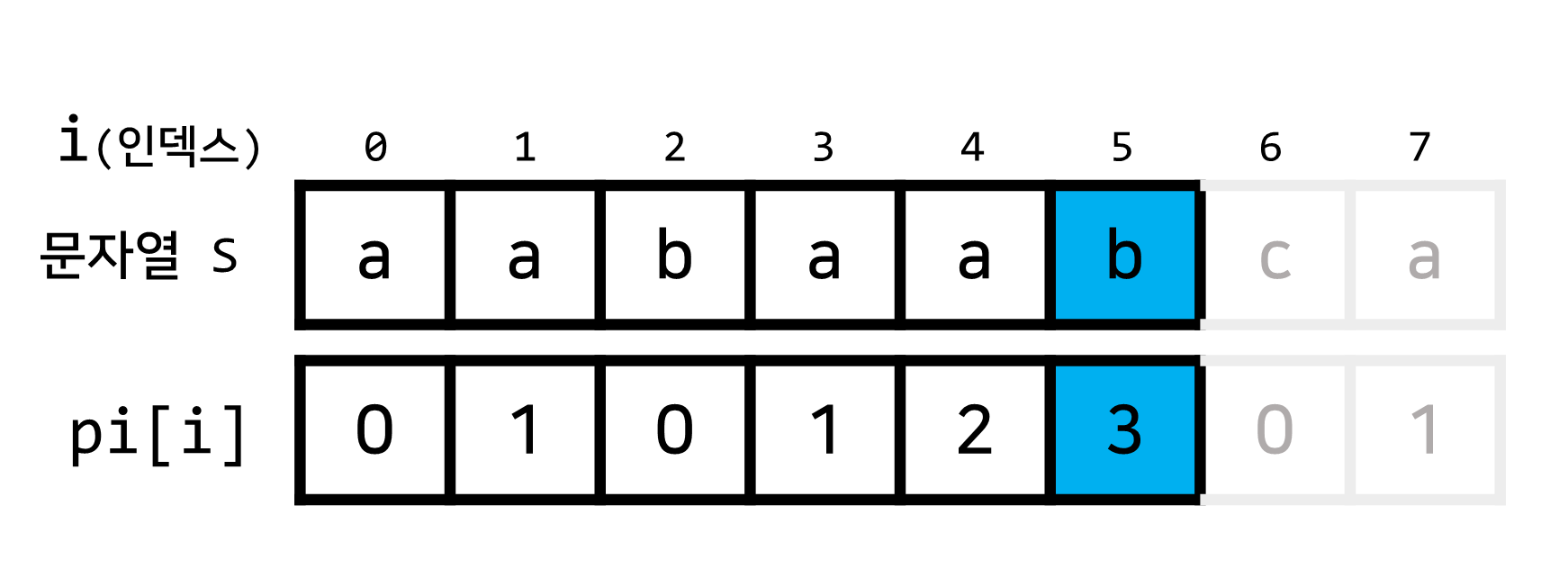
pi[5] = 3, 즉 현재까지의 문자열에서 길이가3인 접두사와 접미사가 서로 일치한다는 정보입니다.- 문자열 S를 기준으로 길이가
3인 접두사는 ▶aab - 문자열 S를 기준으로 길이가
3인 접미사는 ▶aab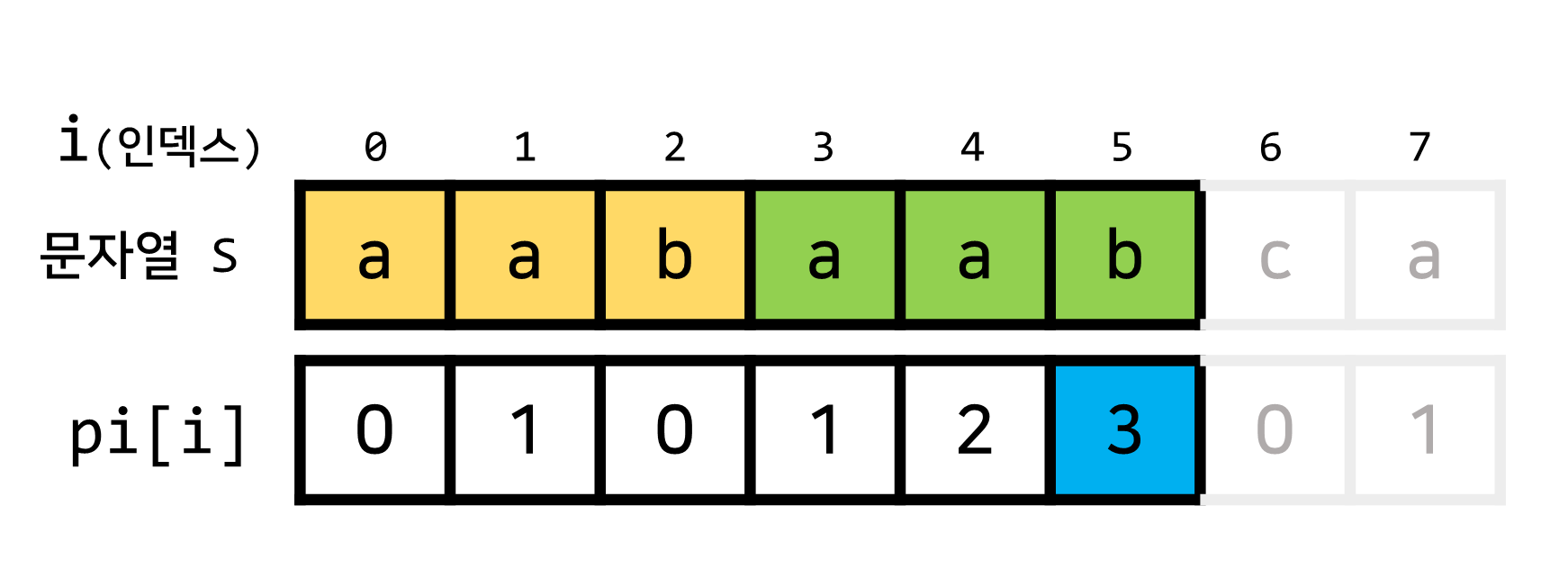 이렇게 말이죠.
이렇게 말이죠.
1.2 pi[] in Python
def get_pi(pattern):
pi = [0 for _ in range(len(pattern))]
# j: 접두사의 마지막 위치를 가리킵니다.
# i: 접미사의 마지막 위치를 가리킵니다.
j = 0
for i in range(1, len(pattern)):
# 만약 접두사와 접미사가 달라지는 지점이 발생하면(S[i] != S[j])
# 과거에 일치했던 접두사가 있었는지 역으로 탐색합니다. (j = pi[j-1])
# 더 이상 탐색할 접두사가 없을 때까지 반복합니다. (while j > 0)
while j > 0 and S[i] != S[j]:
j = pi[j-1]
# 하지만 만약 S[i] == S[j]인 j값을 발견하면,
# 해당 j가 바로 현재까지의 문자열에서 접미사와 일치하는 가장 긴 접두사의 마지막 인덱스 값입니다.
# 즉, 현재까지의 문자열에서 j+1만큼의 길이를 갖는 접두사와 접미사가 서로 일치하겠네요.
if S[i] == S[j]:
pi[i] = j + 1 # ▶ i까지의 문자열 중 길이가 (j+1)인 접두사와 접미사가 일치한다는 의미입니다.
j += 1 # 접두사의 길이를 1 늘려서 다시 일치하는지 확인해봅니다.
return pi
2. KMP
- 저는 KMP 알고리즘을 다음과 같이 이해했습니다.
접두사 만큼의 문자열 탐색을 줄인다.
2.1 KMP 이해하기
2.1.1 예시 상황 설명
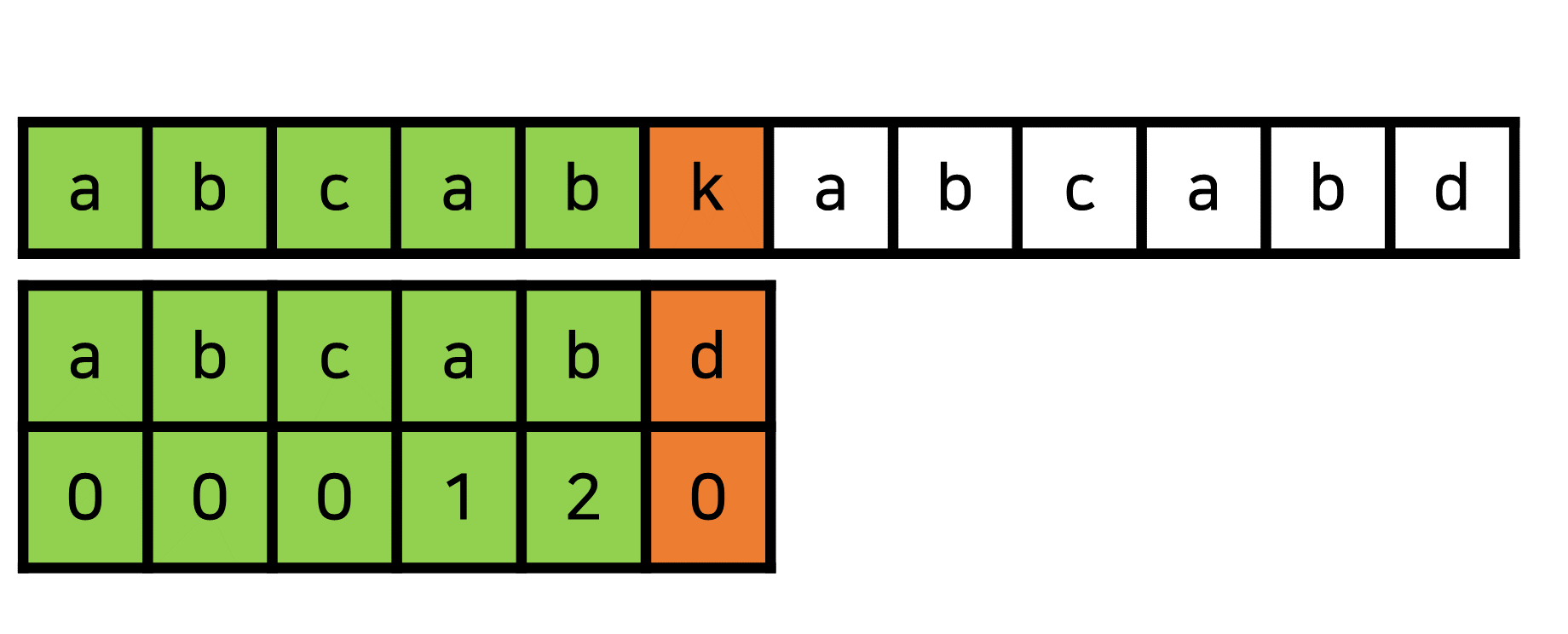
다음과 같이abcabkabcabd에서abcabd를 찾는 과정을 생각해봅시다.
앞의abcab5글자까지는 일치함을 확인했는데, 아깝게 마지막 글자가 다르네요.
이때 아래와 같이 탐색한다면 시간이 매우 오래 걸리겠죠?
이때 어떻게 하면 효율적으로 탐색할 수 있을까요?
2.1.2 KMP 알고리즘의 Key
- 힌트는 바로 여기에 있습니다.
접두사 만큼의 문자열 탐색을 줄인다.
- 이때,
pi[]의 정보를 활용해서 "접두사 만큼의"에 해당하는 정보를 찾을 수 있을 것 같아요.- 현재 위치에서는 실제 문자열과 찾으려는 문자열의 값이 일치하지 않으므로
이전 위치의pi[]를 기준으로 "접미사와 접두사가 일치하는 최대 길이"를 구해봅시다.
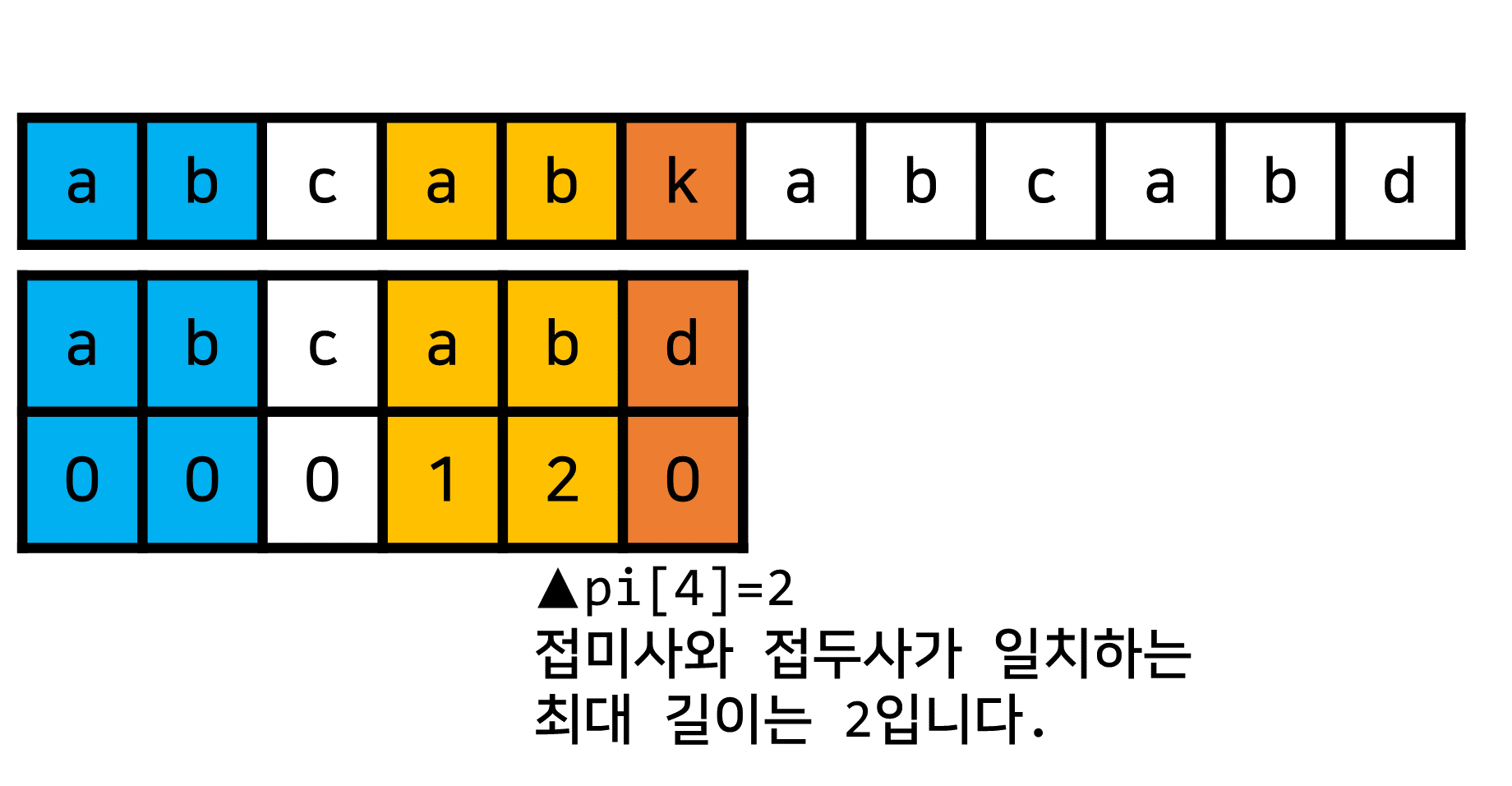
- 현재 위치에서는 실제 문자열과 찾으려는 문자열의 값이 일치하지 않으므로
- 이때, "접두사 만큼의 탐색을 건너뛰어봅시다!"
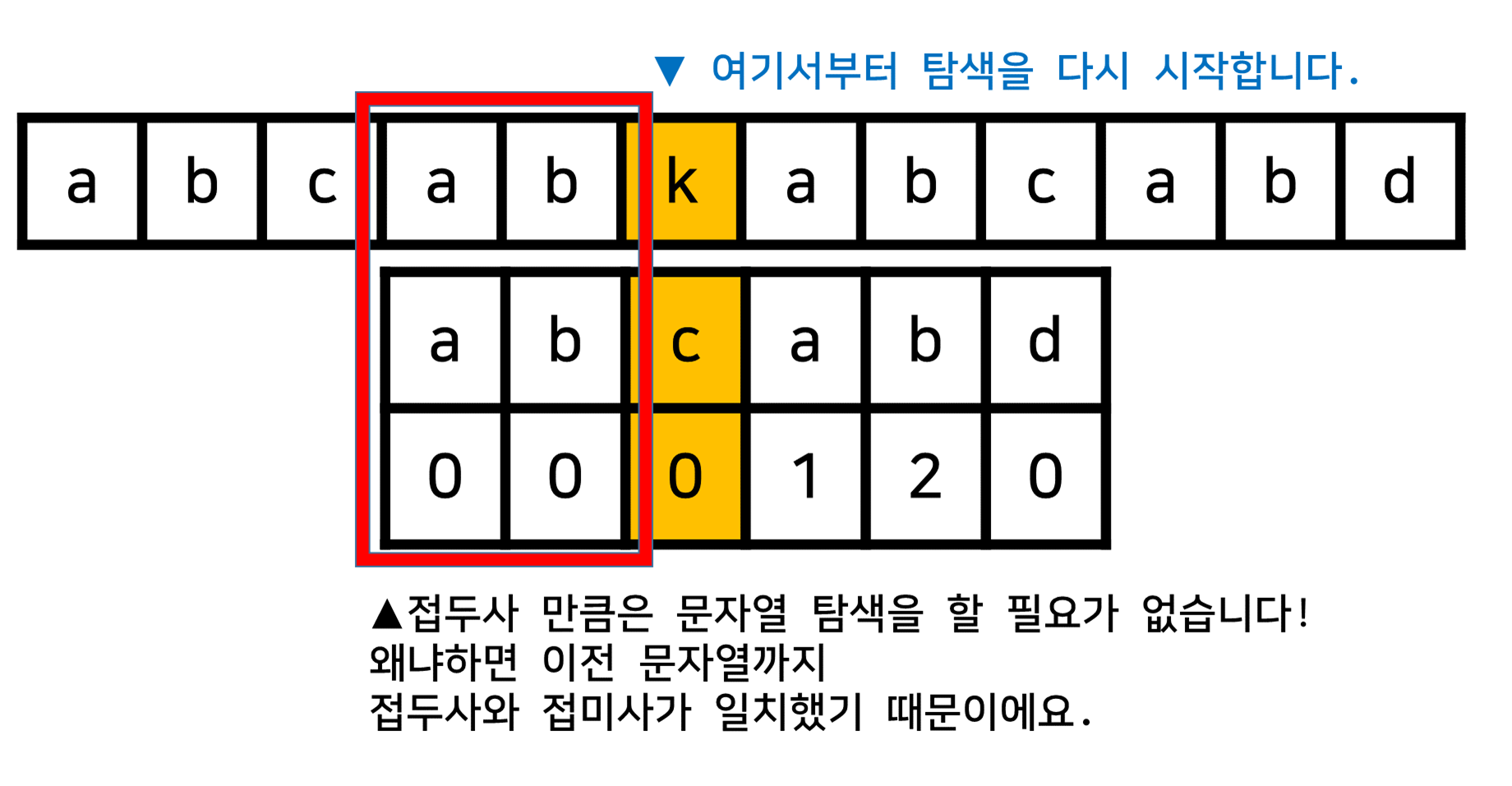
- 이처럼 KMP를 활용하면 "접두사 만큼의 탐색 비용"을 줄일 수 있기 때문에 기존의 브루트포스 방식보다 훨씬 효율적입니다!
2.2 KMP in Python
def KMP(string, pattern):
pi = get_pi(pattern)
# j : pattern을 탐색할 인덱스입니다.
j = 0
for i in range(len(string)):
# 만약 j에서 string과 pattern이 일치하지 않는다면,
# pattern의 "0~j"까지의 부분 문자열 중에서
# 접두사가 존재했던 문자열을 역으로 탐색해가면서(j = pi[j-1])
# 탐색 비용을 최대한 줄여봅니다.
# 따라서 처음부터 탐색하는 것이 아닌, 접두사 이후(=pi[j-1])부터 탐색을 재시작하기 때문에
# ✨"접두사 만큼의 문자열 탐색을 줄일" 수 있습니다.✨
while j > 0 and string[i] != pattern[j]:
j = pi[j - 1]
if string[i] == pattern[j]:
if j + 1 == len(pattern):
print(f"문자열을 찾았습니다! 시작 위치는 {i - j} 입니다.")
j = pi[j]
else:
j += 1KMP 전체 코드 (in python)
def get_pi(S):
pi = [0 for _ in range(len(S))]
j = 0
for i in range(1, len(S)):
while j > 0 and S[i] != S[j]:
j = pi[j - 1]
if S[i] == S[j]:
j += 1
pi[i] = j
return pi
def KMP(string, pattern):
pi = get_pi(pattern)
j = 0
for i in range(len(string)):
while j > 0 and string[i] != pattern[j]:
j = pi[j - 1]
if string[i] == pattern[j]:
if j + 1 == len(pattern):
print(f"문자열을 찾았습니다! 시작 위치는 {i - j} 입니다.")
j = pi[j]
else:
j += 1
string = "bananaisdeliciousheynananabananananabananananbanananaa"
pattern = "anana"
KMP(string, pattern)결과
문자열을 찾았습니다! 시작 위치는 1 입니다.
문자열을 찾았습니다! 시작 위치는 21 입니다.
문자열을 찾았습니다! 시작 위치는 27 입니다.
문자열을 찾았습니다! 시작 위치는 29 입니다.
문자열을 찾았습니다! 시작 위치는 31 입니다.
문자열을 찾았습니다! 시작 위치는 37 입니다.
문자열을 찾았습니다! 시작 위치는 39 입니다.
문자열을 찾았습니다! 시작 위치는 46 입니다.
문자열을 찾았습니다! 시작 위치는 48 입니다.