Find: Path Compression (경로 압축)

• find 연산 수행 시 방문한 노드들에 대해,
  노드들의 부모를 Root로 갱신시켜주는 방법입니다.
• 따라서 다음에 find 연산을 수행했을 때,
  경로를 압축한 노드들에 대해서는 부모값이 이미 Root로 갱신된 상태이므로,
  Root를 찾는 비용을 아낄 수 있습니다.

간단하게 그림으로 이해해봅시다.

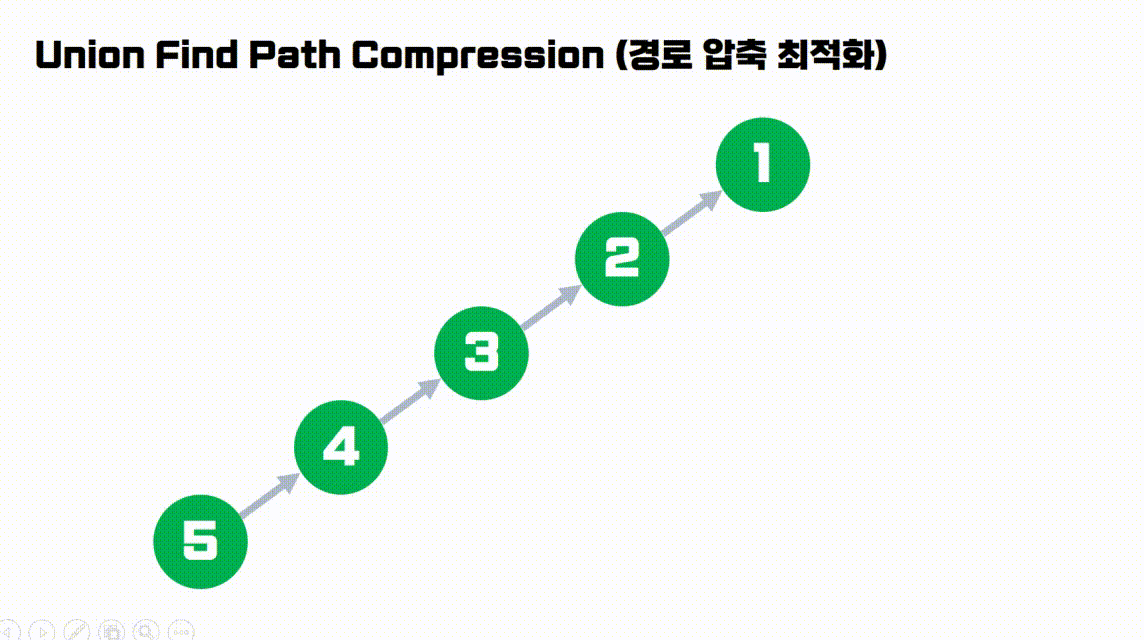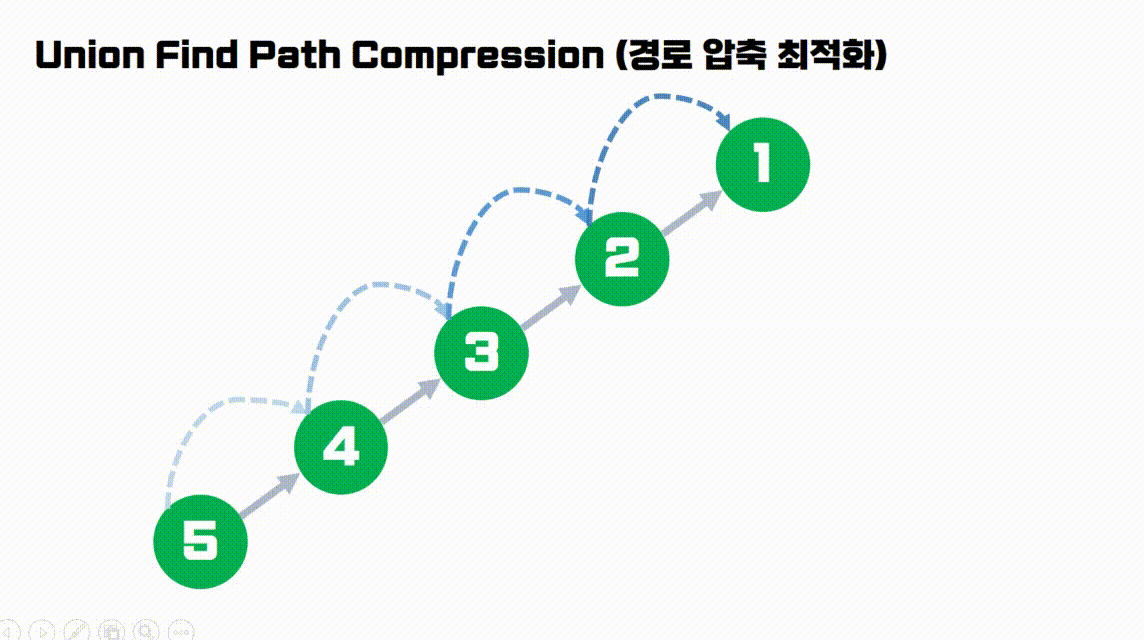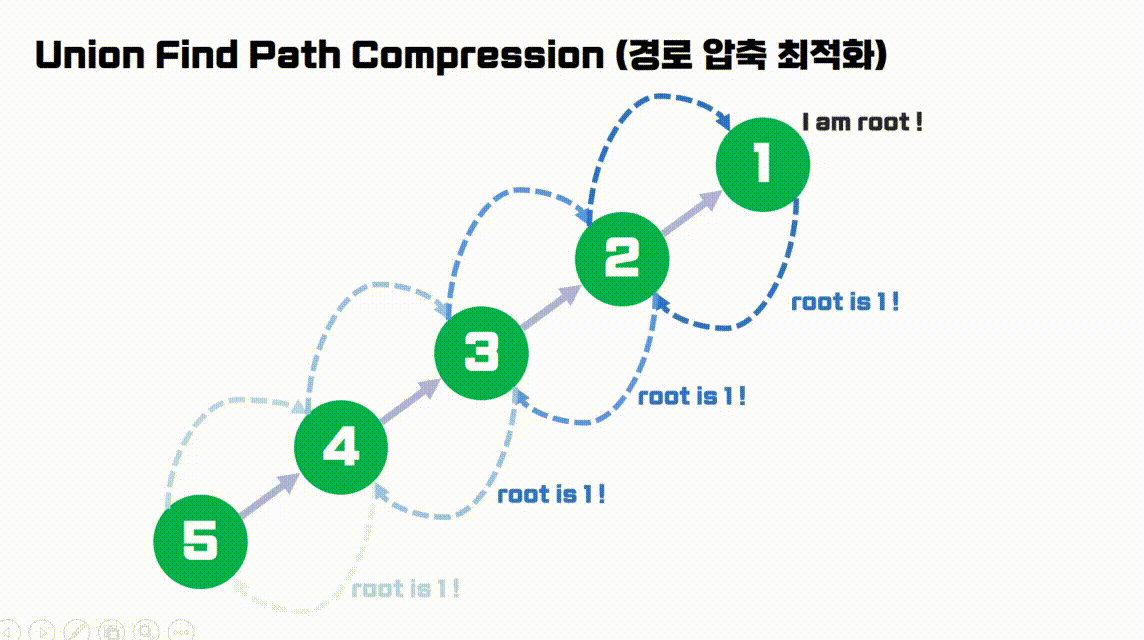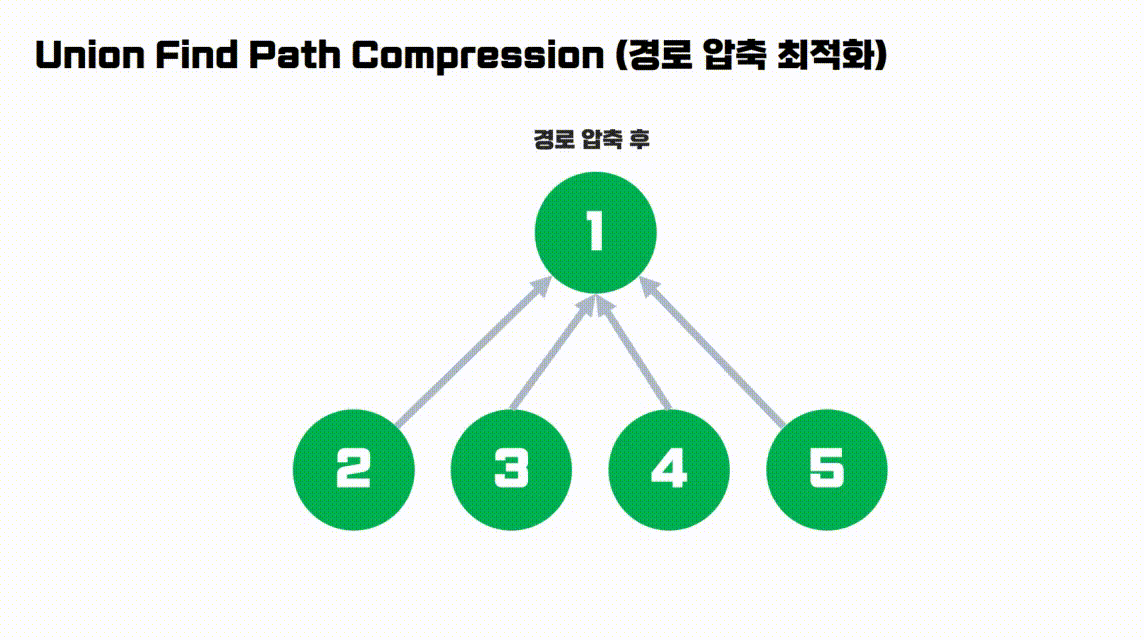
• 다음 예시는 find(5)를 수행한 결과입니다.
• 노드 5번의 Root를 찾는 과정에서 방문한 모든 노드들의 부모를 Root로 갱신해줍니다.
• 따라서 만약 이후에 find(4)를 수행한다면, 이미 Parent가 Root로 갱신된 상태이므로 Root를 찾는 비용을 절약할 수 있습니다.
  

Code (python)

# v라는 노드의 최종 부모(root)를 찾아 반환합니다.
def find(v):
    if parent[v] != v:
        parent[v] = find(parent[v])
    return parent[v]

---

Union: Union By Rank

• 트리의 높이는 탐색의 효율성과도 직접적으로 관련이 있습니다. 따라서 트리의 높이를 항상 작게 유지하는 것이 중요합니다.
• 예를 들어서, 아래 그림 예시를 통해 트리를 어떻게 합치느냐에 따라 탐색의 효율성이 달라짐을 확인할 수 있습니다.
  
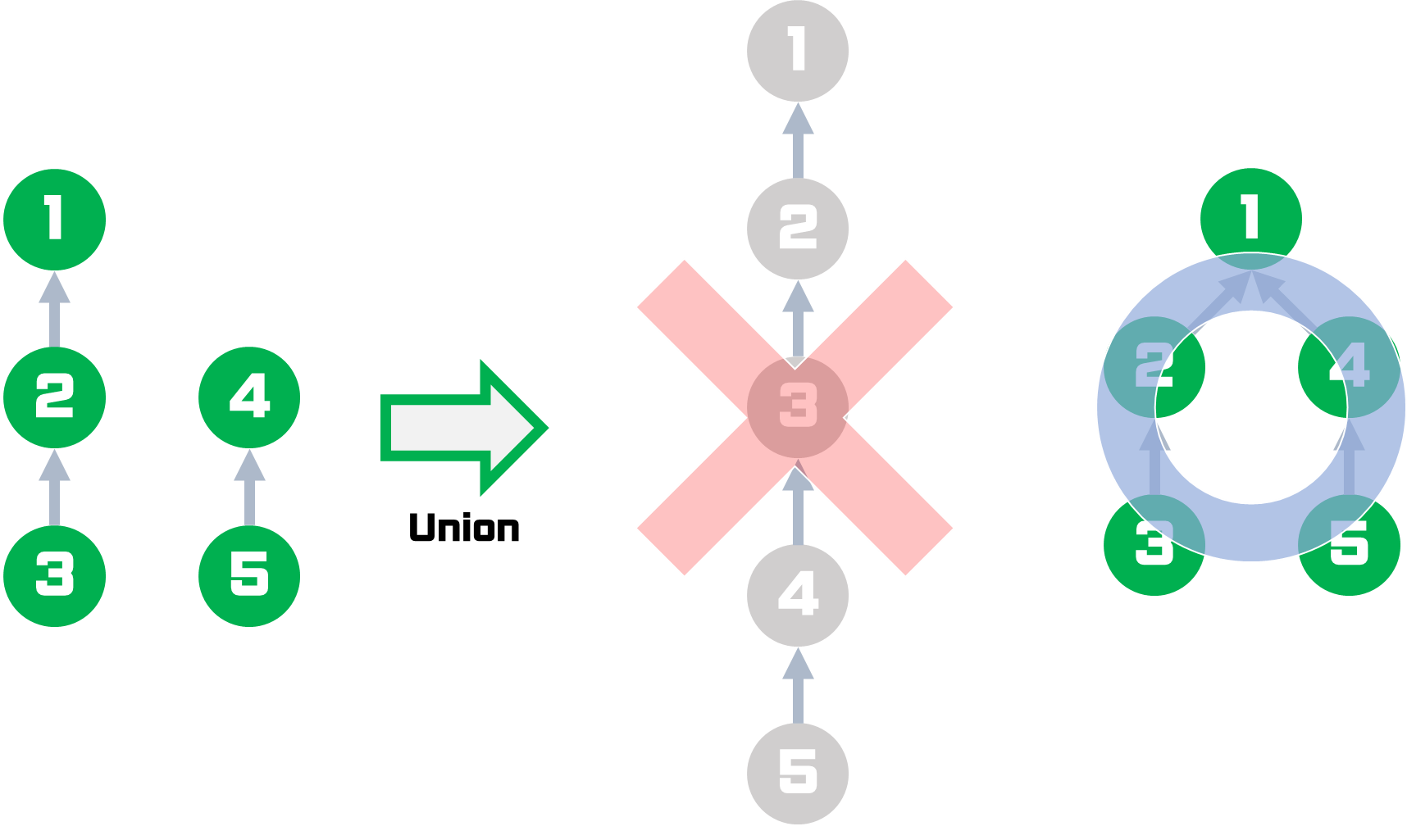
• 따라서, 이를 구현하기 위해 기존 union 방식에 'rank'를 추가합니다.
• rank는 트리의 높이와 관련된 정보를 담고 있습니다.
  하지만 엄밀히 말해서는 실제 트리의 높이와는 다를 수도 있습니다. 왜냐하면 위의 Path Compression에 의해 트리의 높이는 동적으로 변하기 때문이에요. Path Compression에 의해 트리의 높이는 작아질 수 있지만, Rank의 값은 작아질 수 없고 증가만 가능합니다.
• 따라서 이제는 더 작은 rank를 가진 트리가, 더 큰 rank를 가진 트리에 붙는 방식으로 Union을 구현할 것입니다.

간단하게 그림으로 이해해봅시다.

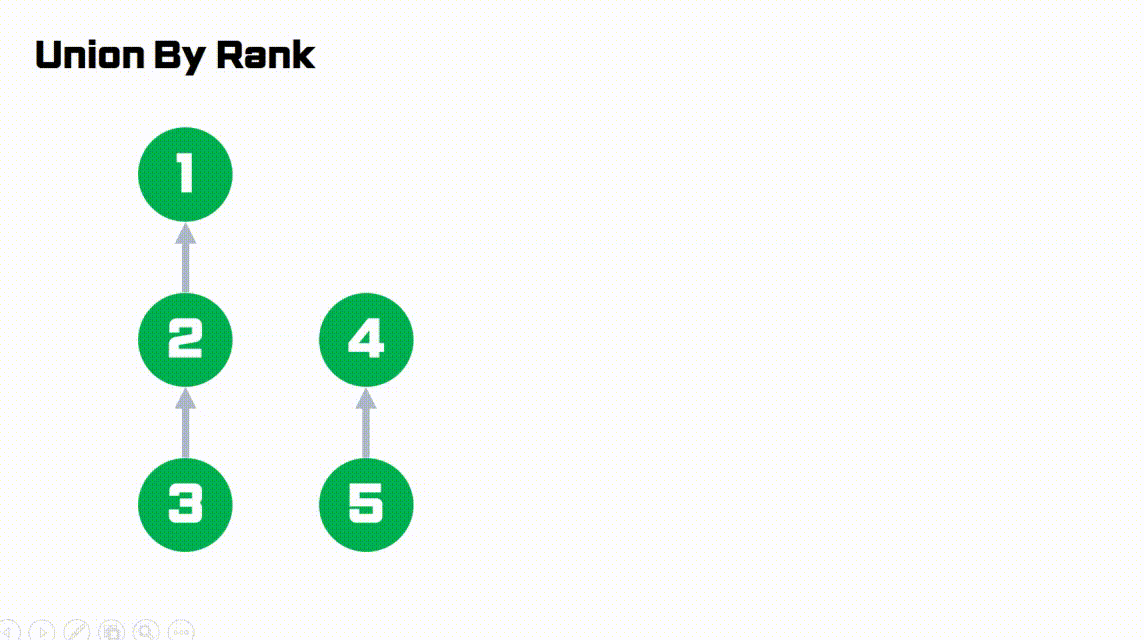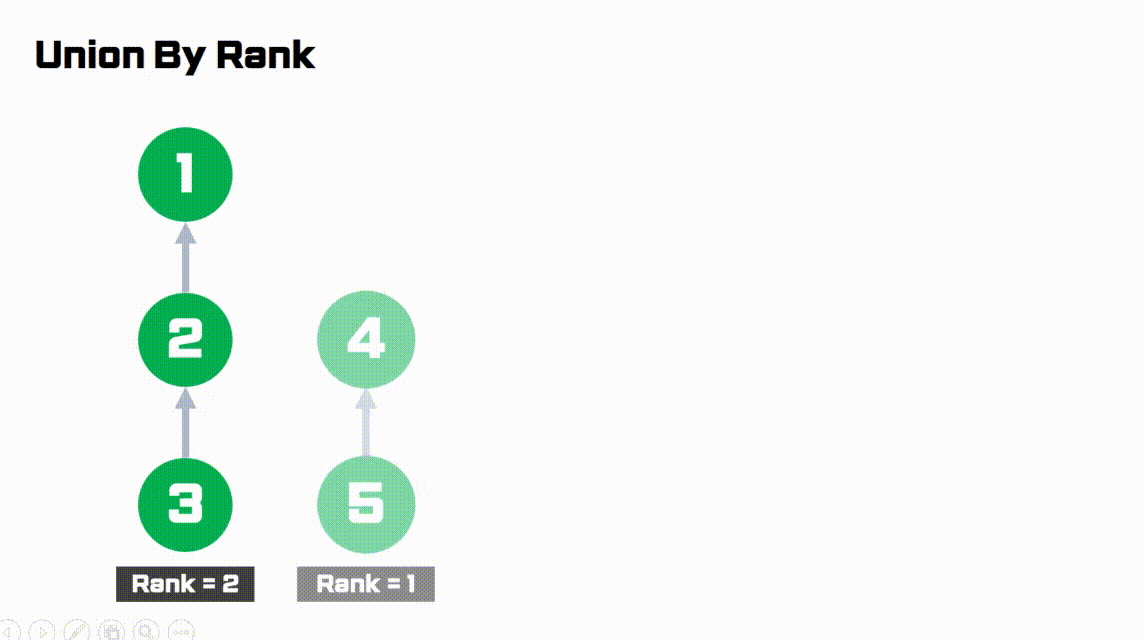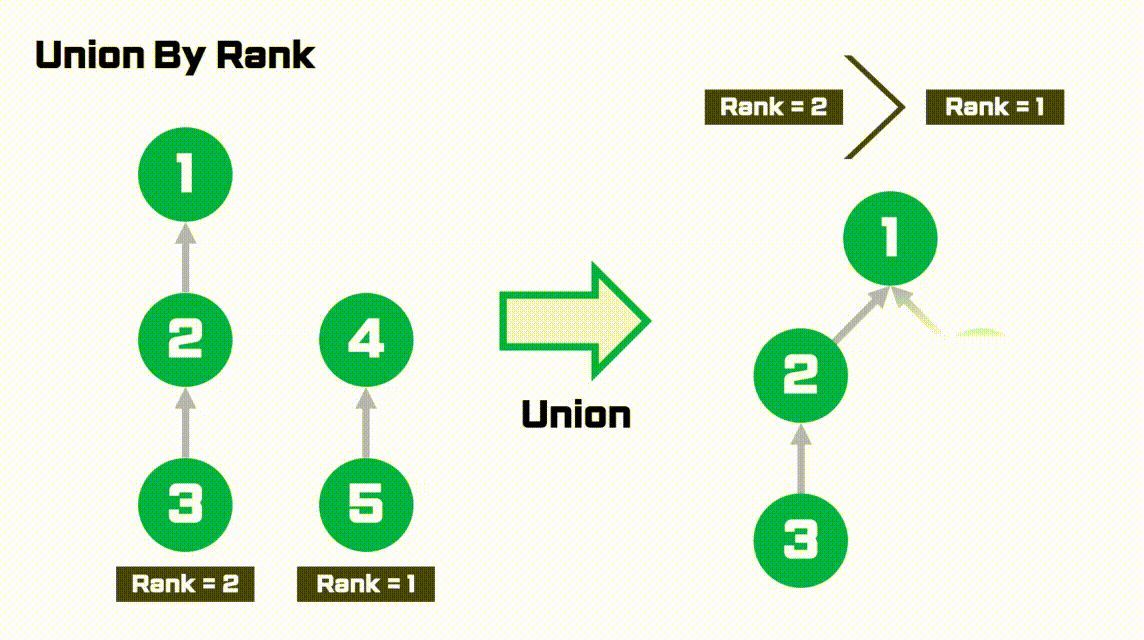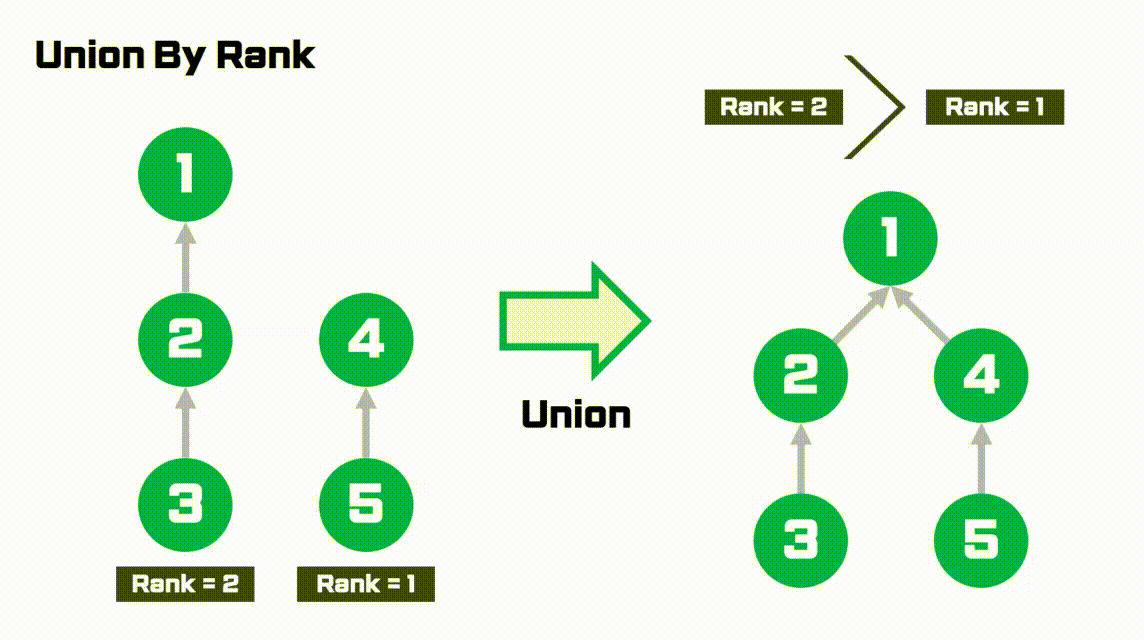
• rank가 1로 더 작은 오른쪽 트리가
  rank가 2로 더 큰 왼쪽 트리에 붙습니다.
• 따라서 트리의 높이를 작게 유지할 수 있습니다.
  

Code (python)

def union_by_rank(v1, v2):
    p1 = find(v1)
    p2 = find(v2)

    # 같은 집합(트리)에 포함되어 있는 경우입니다.
    if p1 == p2:
        return

	# rank가 큰 트리에 작은 트리를 붙입니다.
    if rank[p1] > rank[p2]:  
        parent[p2] = p1
    elif rank[p1] < rank[p2]:
        parent[p1] = p2
    else:  # 만약 rank가 같다면 임의로 p1 트리에 p2 트리를 붙입니다.
        parent[p2] = p1
        rank[p1] += 1

---

Kruskal Algorithm

• 최적화한 Union Find 방법으로 크루스칼 알고리즘을 구현해봅시다.
• 문제는 BOJ 1197: 최소 스패닝 트리 입니다.

def find(v):
    if parent[v] != v:
        parent[v] = find(parent[v])
    return parent[v]


def union_by_rank(v1, v2):
    p1 = find(v1)
    p2 = find(v2)

    # rank가 큰 트리에 작은 트리를 붙입니다.
    if rank[p1] > rank[p2]:
        parent[p2] = p1
    elif rank[p1] < rank[p2]:
        parent[p1] = p2
    else:  # 만약 rank가 같다면 임의로 p1 트리에 p2 트리를 붙입니다.
        parent[p2] = p1
        rank[p1] += 1


def kruskal():
    total_weight = 0

    # [1] 간선들을 가중치가 작은 순서대로 오름차순 정렬합니다.
    edges.sort()

    # [2] 간선들을 하나씩 추출하여 연결합니다.
    for weight, v1, v2 in edges:
        if find(v1) != find(v2): # 같은 집합(트리)에 포함되어 있는 경우에는 Union할 수 없습니다. 사이클이 생기기 때문이에요. 
            union_by_rank(v1, v2)
            total_weight += weight

    return total_weight

# 입력 및 실행
V, E = map(int, input().split(" "))

parent = [i for i in range(V + 1)]
rank = [0 for _ in range(V + 1)]

edges = []
for _ in range(E):
    v1, v2, w = map(int, input().split(" "))
    edges.append([w, v1, v2])

answer = kruskal()
print(answer)