Linear Regression

Linear Regression

선형회귀라고 불리는 Linear Regression은 가장 기본적인 머신러닝 알고리즘으로 각 Feature들간의 선형조합(Linear Combination)을 통해 이루어진 모델을 학습시키는 것을 의미합니다. 모델자체가 데이터와 상관없이 선형적인 수식으로 학습되기 때문에 다른 모델들과 비교했을때 상대적으로 높은 bias(세상에는 단순 선형으로 표현가능한 것이 별로 없겠죠?)와 낮은 variance(직선이므로 유연하지 않습니다.)를 가지는 형태가 됩니다. 참고로 bias와 variance는 둘다 낮을수록 좋습니다.

그럼에도 Linear Regression은 굉장히 자주 사용되는데 그 이유는 한번 학습하면 굉장히 적은 computational cost를 가지고 예측이 가능하고 학습도 빠르고, 모델의 피처별 coefficients를 확인함으로써 상대적인 피처간 중요도를 파악하거나 모델 자체를 해석하기 용이하기 때문입니다.

• 분류 : Supervised learning
• 형태 : Linear Model
• 용도 : Regression
• 장점 : 간결함(베이스라인), 해석가능성(Interpretablilty), 효율성(Efficiency)
• 단점
  • 피처간 낮은 상관관계(low-correlation)을 가정 (높은 independence)
  • 너무 간단한 형태의 모형으로 underfitting의 위험성
  • 아웃라이어(outlier)에 취약

1. Model

다음과 같이 $N$개의 피처벡터 $\textbf{x}$와 라벨 $y$의 집합이 있다고 가정해봅시다. 그냥 N개의 샘플데이터(observation)로 구성된 dataset입니다.

여기서 $\textbf{x}$는 다수의 피처(feature)를 지닌 벡터로 각 피처를 $x$라 할때 다음과 같이 나타낼 수 있고 $j$는 각 피처를 가리키는 인덱스입니다.

각 $\textbf{x}$의 각 피처의 parameter 혹은 coefficient 벡터를 $\textbf{w}$라 하고 bias를 $b$라 한다면 다음과 같은 선형결합 모델을 표현할 수 있고 이를 다음과 같이 표현하면 수식이 완성됩니다. 여기서 각 피처의 선형결합은 $w_1x_1 + w_2x_2 + w_3x_3, ...\:, +w_jx_j$ 형태이므로 벡터 간의 내적(dot-product) 형태로 표현할 수 있습니다. 참고로 여기서 $\textbf{x}$ 와 $\textbf{w}$는 모두 길이가 j인 벡터입니다. (벡터의 내적은 동일한 길이의 벡터끼리만 가능)

이 방정식(모델)을 학습시켜 얻게되는 최종 $\textbf{w}^*$와 $b^*$ 를 기반으로 신규 데이터 $\textbf{x}^{new}$에 따라 결과 값 $y^{new}$의 값을 예측(predict)할 수 있게 됩니다. 간단하지요?

그렇다면 최적의 $\textbf{w}^*$와 $b^*$은 어떻게 도출해야할까요?

2. Objective Function

최적의 $\textbf{w}^*$와 $b^*$을 찾아내기위해서는 먼저 목적함수(Objective function)을 정의해야 합니다. 목적함수란 최적의 파라미터값을 찾기 위해 수학적으로 Maximize 혹은 Minimize해야하는 수식을 의미합니다.

여기서 목적함수는 다음과 같이 각 샘플의 결과와 실제 결과의 오차의 제곱합인 square error loss 오차함수(Cost function)를 이용하도록 하여 작성하도록 하겠습니다.

다음과 같이 목적함수 내에서 다음과 같이 하나의 샘플에 대한 오차 값을 표현하는 수식은 오차함수(Cost function)라 합니다.

오차함수는 이 외에도 오차의 절대값을 의미하는 absolute error등 다양하게 정의될 수 있습니다. 하지만 square error loss는 미분가능한 함수로 수학적으로 편리하며, absolute error이 비해 오차에 대해 제곱을 취함으로써 아웃라이어에 대한 penalizing을 극대화시키는 효과가 있어 자주 사용됩니다.

3. Optimization

목적함수를 정의하였으면 이를 최소화할 수 있는 변수 $\textbf{w}$와 $b$를 찾으면 되는데 이를 위해서는 경사하강법(Gradient descent)이 가장 유명한 방법입니다.
다만 경사하강법을 사용하여 global minimum을 찾는 것을 보장하기 위해서는 목적함수의 형태가 convex하여야 합니다.

먼저 목적함수가 어떻게 생겼는지를 보기위해 편의상 피처($\theta_1$)를 1개로 두고 피처-error의 간 의 그래프를 그려봅시다.

import numpy as np
import matplotlib.pyplot as plt

def objective_function(theta_1, x, y):

    error = y - theta_1 * x
    squared_error = np.square(error)
    sum_squared_error = np.sum(squared_error)
    
    return sum_squared_error

x = np.array([1, 2, 3, 4, 5])
y = np.array([3, 5, 7, 9, 11])

theta_1_range = np.linspace(-10, 10, 100)

objective_values = np.zeros_like(theta_1_range)
for i in range(len(theta_1_range)):
    objective_values[i] = objective_function(theta_1_range[i], x, y)

plt.plot(theta_1_range, objective_values)
plt.xlabel('theta_1')
plt.ylabel('Error')
plt.title('Objective Function')
plt.grid(True)
plt.show()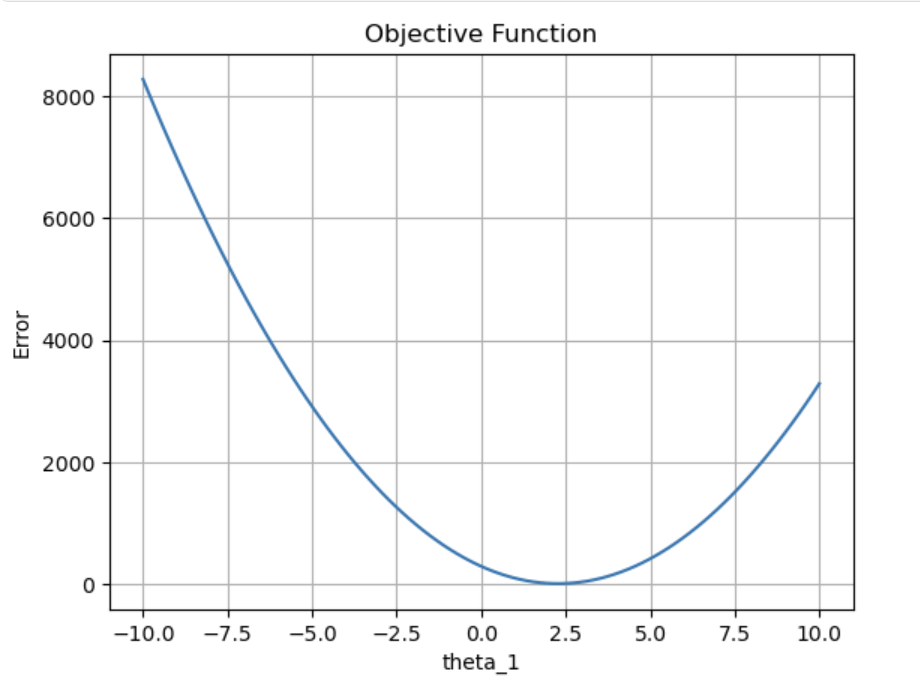

다음과 같이 global-minimum을 가지는 경우 경사하강법을 이용해서 구할 수 있습니다.

4. Code

sklearn을 이용하면 코드 구현은 매우 간단합니다.
우선 임포트 부터 성능평가(RMSE)까지 기본 옵션으로 쭉 표현하면 다음과 같습니다.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

model = LinearRegression()
model.fit(X_train, y_train)
pred = model.predict(X_test)
mse = mean_squared_error(y_test, pred, squared=False)

학습된 모델의 계수와 편차를 확인하고 싶으면 다음과 같이 확인할 수 있습니다.
값은 numpy array의 형태로 출력됩니다.

model.coef_ # 모델의 각 계수 (w)
model.intercept_ # y절편 (b)

5. Similar Model

5.1. Ridge

Linear Regression에 L2정규화를 적용한 모델입니다.

from sklearn.linear_model import Ridge

5.2. Lasso

Linear Regression에 L1정규화를 적용한 모델입니다.

from sklearn.linear_model import Ridge

5.3. Elastic Net

Ridge와 Lasso의 중간 형태

from sklearn.linear_model import ElasticNet