Counting

"Step" rule of counting

set이 여러 스텝의 걸쳐 일어날 경우 각 set 크기를 계산하여 곱합니다. 예를 들어 12픽셀크기의 해상도가 표현할 수 있는 그림의 수를 카운팅해야한다고 가정하고 한 픽셀의 할당될 수있는 색을 다음과 같이 표현합니다.

그렇다면 set $A$의 크기 $|A|$는 100이 되므로 하나의 스텝의 경우의 수는 100이 됩니다. 다음 스텝도 동일하게 100이고 모든 스텝이 동일하게 진행되네요. 그렇다면 총 12스텝에 걸쳐 발생하므로 답은 $100^{12}$가 됩니다.

다만, Step rule의 constraint는 이전 스텝에서 어떤 선택을 하느냐에 따라 다음 선택의 결과가 달라지지 않아야 한다는 것입니다. 다음 스텝의 set의 크기가 이전 스텝의 크기와 달라지는 것은 상관하지 않습니다.

"OR" rule of counting

서로 "mutual independent"한 set들을 counting 할때는 각 set의 크기를 합해주면 됩니다. 예를 들어 축구공 5개와 농구공 3개가 있는데 이 중 하나를 선택하는 경우를 고르자면 $|fb| = 5, |bb| = 3$ 이므로 $|fb|+|bb|=8$의 경우의 수가 나오게 됩니다.
다만 OR rule의 constraint는 상호 독립(mutual independence)이므로 제약조건이 까다롭습니다.

만약 두 set이 mutual independent하지 않아 overlapping(double-counting)되는 부분이 있다면 이 부분을 제거해 주고 세면 됩니다.

Sort, order matters (Permutation)

Counting Table

카운팅문제에 대한 공식 테이블을 정리해보았습니다.
row는 replacement에 대한 유무, column은 order matter에 대한 유무입니다.

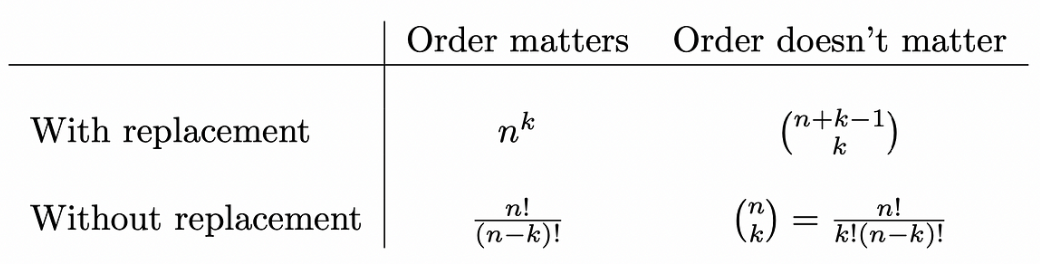
1. With replacement, Order matter

n개 중 k개를 뽑습니다. 뽑고 다시 넣는 것을 with repacement라 합니다.
그렇게 되면 시행횟수는 매번 n번의 새로운 경우의 수가 발생하므로 $n^k$가 됩니다.

2. Without replacement, Order matter

n개 중 k개를 뽑습니다. 뽑은 대상들의 순서는 중요하며, 뽑은 대상을 다시 후보군에 넣지 않습니다.
이는 전형적인 Permutation 순열문제이며 $_nP_k$ 라고도 표기합니다.
처음에는 n개의 경우의수, 두번째는 하나를 뽑았으므로 n-1개의 경우의수 ... k번째까지 뽑게 됩니다. 즉 k개의 항이어야 하므로 n-k+1까지 곱해줍니다.

이는 팩토리얼 수식으로 다음과 같이 표현됩니다.

3. With replacement, Order doesn't matter

가장 어려운 경우입니다. n개 중 k개를 뽑습니다. 하지만 한번 뽑은 오브젝트를 넣으며(replace) 순서는 중요하지 않습니다.

n개의 distinguishiable 박스와 그 박스 내의 k개의 indistingushable 점들을 상상해 봅시다.

n = 2이고 k = 6이라면 다음과 같이 구분될 수 있습니다.
박스가 2개이므로 separator "|"는 하나로 표시됩니다. n-1개죠.
..... | .

n = 3이고 k = 4라면 다음과 같은 형태로 나타나는 경우가 있을 겁니다.
.. | . | .

즉 이는 총 n+k-1개의 .과 |을 나열해서 k개의 .을 뽑아내는 경우의 수를 의미합니다. 즉 choose k out of (n-1) + k입니다.
이는 곧 다음과 같습니다.

4. Without replacement, Order doesn't matter

n개 중 k개를 뽑는데 뽑은 대상들의 순서는 중요하지 않습니다.
처음에는 순열의 케이스 처럼 $n$부터 $n-k+1$까지 곱해줍니다.
그리고 뽑혀진 k개의 대상들의 순서가 중요하지 않기 때문에 $k!$으로 나누어줍니다.
수식은 다음과 같습니다.

References

[1] Standford Statistics 110
[2] Stanford CS109 Probability for Computer Scientists