[백준] 11729번 : 하노이탑 이동 순서 & 1914번 : 하노이 탑

---

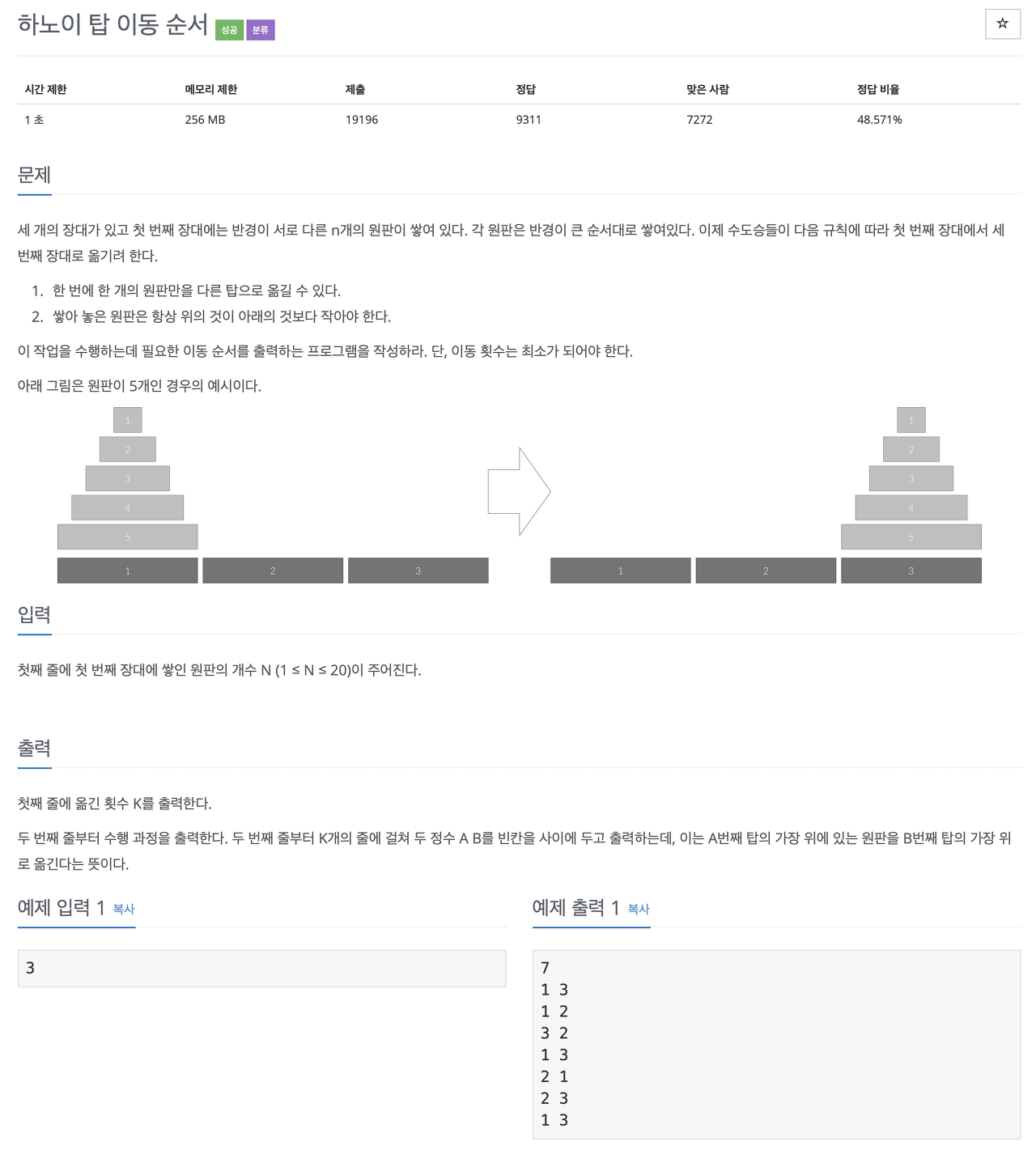
하노이 탑 원판 이동 횟수 공식 유도

하노이의 탑 문제는 재귀 호출을 이용하여 풀 수 있는 가장 유명한 예제 중의 하나이다.
알고리즘 문제를 많이 접해보지 못한 나로서는 하노이 탑 원판 이동 횟수 공식을 풀어보지 못해 이번 기회를 통해 정리 해보려고 한다.

1. 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
2. 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.

이 2개의 규칙을 따르면서 다른 기둥으로 옮기기 위한 과정을 수열로 표현 가능해야 한다.

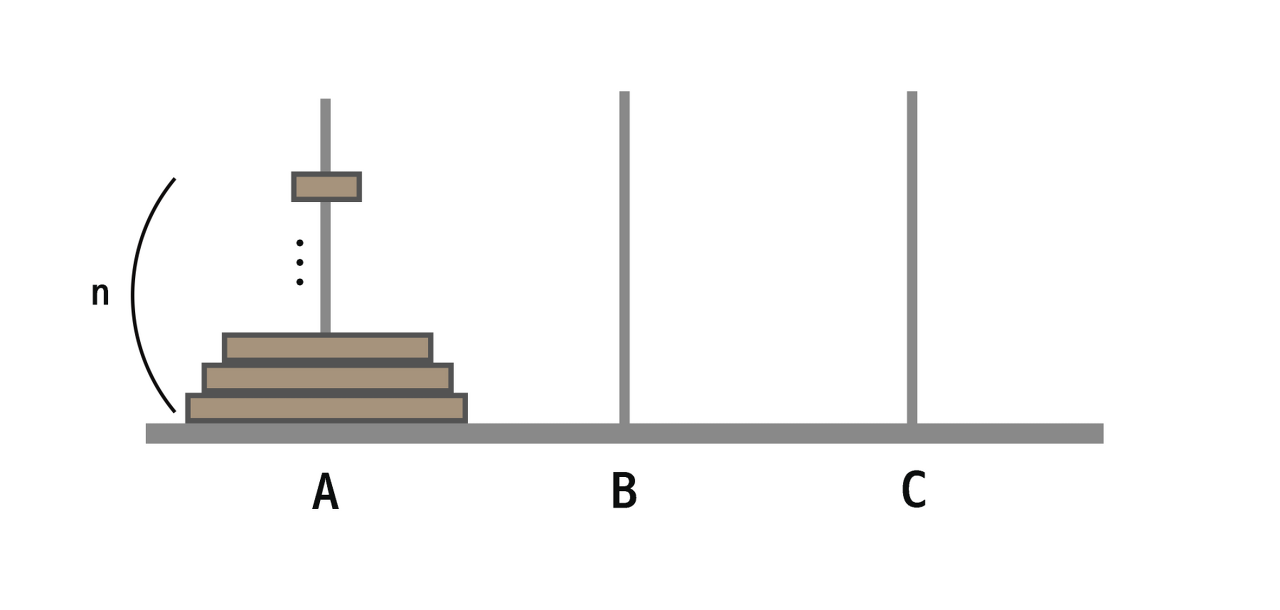
밑에 그림과 같이 n개의 원판이 있다고 가정한다.

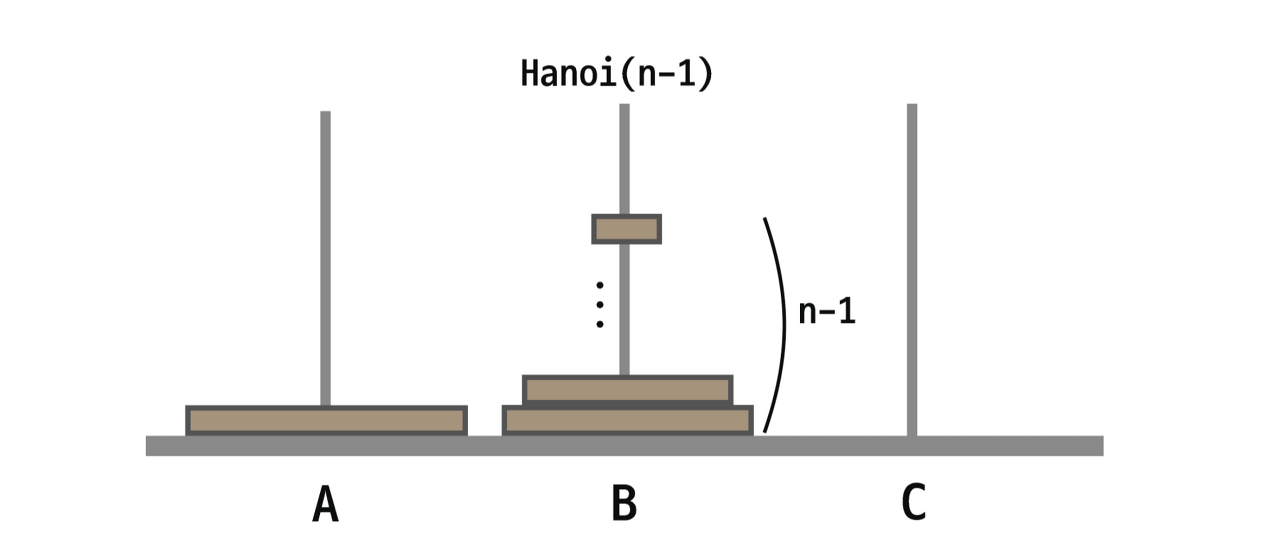
1. 가장 큰 원판을 C 로 옮기기 위해서는 n-1 개의 원판이 A 에서 B 로 가야한다.

n-1번 만큼 B로 가기위한 같은 반복을 할 것이다.
A->B 로의 이동을 Hanoi 함수라고 한다면, n-1 만큼 반복하는 것이다.
그래서 이동 횟수는 다음 그림과 같이 Hanoi(n-1)로 표현한다.

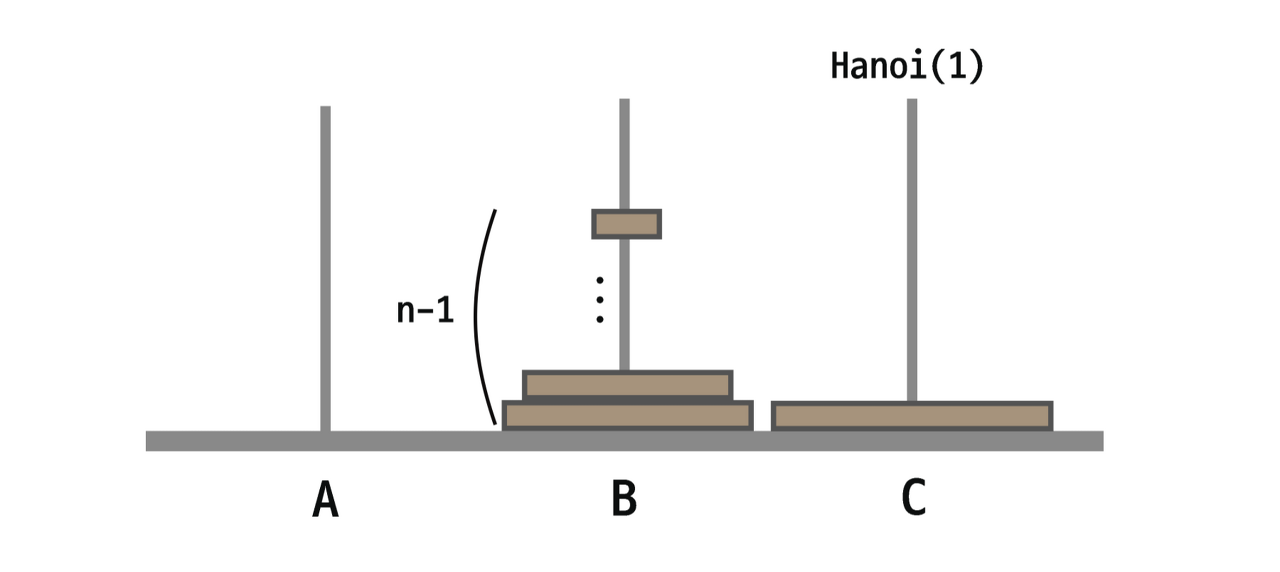
2. 그리고 A 에 있는 가장 큰 원판이 C 로 이동한다.
가장 큰 원판 하나만 이동하기에 - 이동 횟수 1

3. B 에 있는 (n-1)개의 원판을 C 로 이동한다.

1번에서와 같이, B에서 C로의 이동 횟수는 Hanoi(n-1)가 된다.

위에 3개의 과정을 공식화 해보면

Hanoi(n) = Hanoi(n-1) + 1 + Hanoi(n-1)
= 2Hanoi(n-1) + 1
이 된다.


이를 수학적으로 표현해 보면
$a_{n} = 2a_{n-1} + 1$ 이 된다.


이를 귀납적으로 정의 해보겠다.

위의 수식을 통해 다음을 구할 수 있다.
$a_1 = 1 , a_{n+1} = 2a_n+1$

위의 식에서 양변에 1을 더해 다음과 같이 정리할 수 있다.
$a_{n+1} +1 = 2(a_n+1)$

임의의 $b_n$을 잡아서 $b_n = a_n +1$로 가정한다.
$b_{n+1}=2b_n$

그러면 공비가 2인 관계로 표현 가능해진다.

$b_1 = a_1+1 = 2$
이렇게 b1이 2임을 구할 수 있다.

따라서 첫째항이 2이고, 공비가 2인 '공비수열'이 된다.
이를 정리해보면

$b_n = a_n+1 = 2^n$
$a_n = 2^n-1$

이렇게 이 공식의 일반항을 구할 수 있다.

---

이제 구현을 해보겠다.

최종 코드

import java.io.*;

public class Main {
    public static StringBuilder sb = new StringBuilder();
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());

        sb.append((int) Math.pow(2, n) - 1); //총 이동횟수
        if(n<=20) {
            sb.append("\n");
            Hanoi(n, 1, 2, 3);
        }
        System.out.println(sb);
    }
    public static void Hanoi(int n,int start,int mid,int end) throws IOException{

        //이동할 원판 수가 1개일 때 -> 이동 과정 출력
        if(n==1){
            sb.append(start + " " + end + "\n");
            return;
        }
        //A->C로 n-1개 이동
        //start 지점의 n-1개의 원판을 mid 지점으로 이동
        Hanoi(n-1,start,end,mid);

        //제일 큰 원판을 end 지점으로 이동
        sb.append(start + " " + end + "\n");

        //B->C로 n-1개 이동
        //mid 지점의 n-1개의 원판을 end 지점으로 이동
        Hanoi(n-1,mid,start,end);
    }
}

---

추가

백준 1914번 하노이탑

이 문제 또한 같은 문제인데 수가 늘어남에 따라 int가 표현할 수 있는 범위를 벗어나기 때문에 BigInteger를 사용해서 해결 가능했다.
문제 자체 해결은 같음.

import java.io.*;
import java.math.BigInteger;

public class Main {
    public static StringBuilder sb = new StringBuilder();
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BigInteger res = new BigInteger("1"); //
        int n = Integer.parseInt(br.readLine());

        if(n<=20) {
            sb.append((int)(Math.pow(2, n) - 1)).append("\n"); //총 이동횟수
            Hanoi(n, 1, 2, 3);
            System.out.println(sb);
        } else { //20보다 큰 경우
            for(int i=0;i<n;i++){
                res = res.multiply(new BigInteger("2"));//2의 n제곱
            }
            res = res.subtract(new BigInteger("1"));//빼기 1
            System.out.println(res);
        }

    }
    public static void Hanoi(int n,int start,int mid,int end) throws IOException{

        //이동할 원판 수가 1개일 때 -> 이동 과정 출력
        if(n==1){
            sb.append(start + " " + end + "\n");
            return;
        }
        //A->C로 n-1개 이동
        //start 지점의 n-1개의 원판을 mid 지점으로 이동
        Hanoi(n-1,start,end,mid);

        //제일 큰 원판을 end 지점으로 이동
        sb.append(start + " " + end + "\n");

        //B->C로 n-1개 이동
        //mid 지점의 n-1개의 원판을 end 지점으로 이동
        Hanoi(n-1,mid,start,end);
    }
}