N-Queen 문제
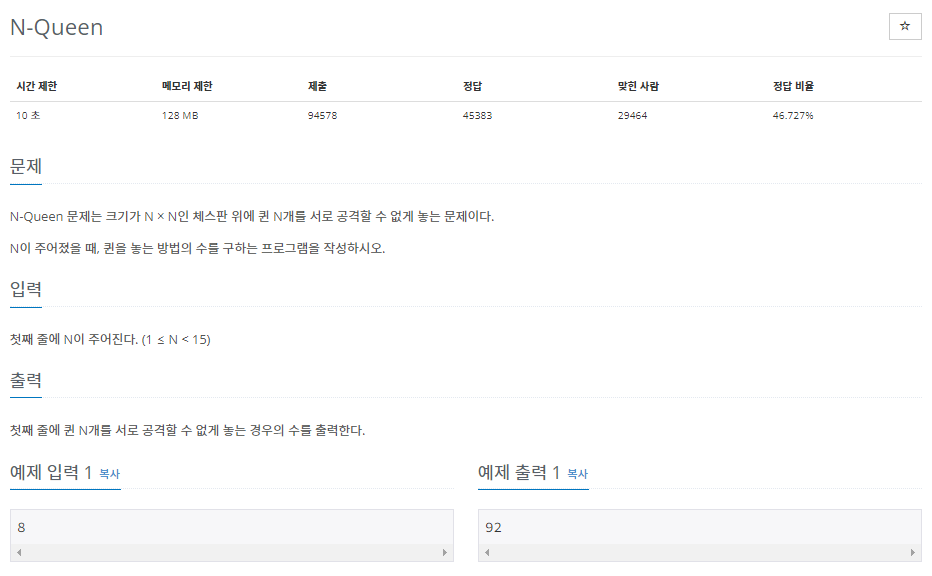
아래 그림에서처럼 상하좌우, 대각선 방향으로 끝까지 공격할 수 있기 때문에 해당 경로에는 퀸을 배치할 수 없다.
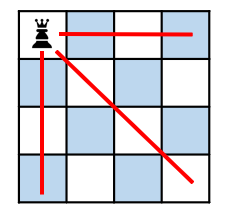
N-Queen 문제는 N의 크기가 작다면 DFS 방식으로 모든 경우의 수를 탐색하면 답을 찾을 수 있다. 하지만 N의 크기가 커질 수록 탐색할 경우의 수가 기하급수적으로 증가한다.
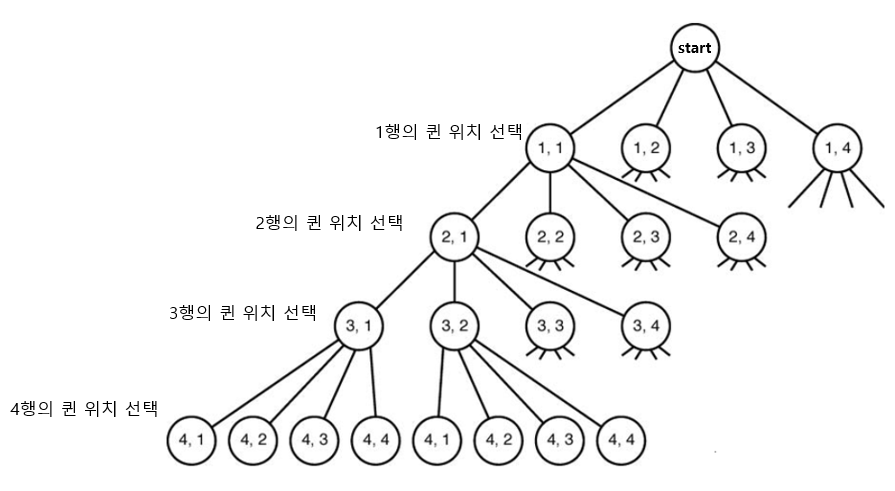
위 그림은 4x4 퀸 문제에서의 상태 공간 트리를 나타낸 것이다. 상태 공간 트리란 모든 가능한 후보 해결법을 트리로 나타낸 것이다. 위와 같은 모든 경우의 수, 즉 퀸을 모든 위치에 배치해보는 방법은 이 걸린다. 즉 매우 비효율적임.
백트래킹(Backtracking)이란?
- 해를 찾는 도중 해가 아니어서 막힌다면, 되돌아가서 다시 해를 찾아가는 기법이다.
- 해를 찾는 도중, 현재 경로가 해가 될 것 같지 않다고 판단했다면 더이상 가지 않고 되돌아간다. 이것을 가지치기(Pruning) 이라고 한다.
- 모든 가능한 경우의 수 중에서 특정 조건을 만족하는 경우만 살펴보면 된다.
백트래킹을 이용한 가지치기
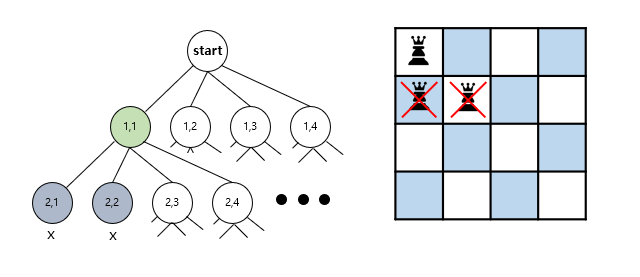
(1,1)에 퀸을 배치하고, 2행에서 어디에 퀸을 배치할 지 결정한다고 한다. (2,1)은 직선상이고, (2,2)는 대각선상이라서 해가 될 수 없는 경로기에 해당 노드로 경로를 탐색하지 않는 Pruning을 적용한다.
이후 (2,3)을 선택한다고 가정해보자.
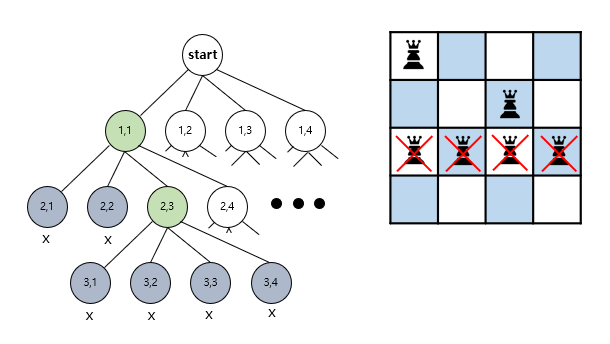
위 그림을 보면 3행에는 아무데도 퀸을 배치할 수 없다. 따라서 이 경로를 더 이상 탐색하지 않고, 다시 2행으로 돌아가 (2,4)를 선택한다.
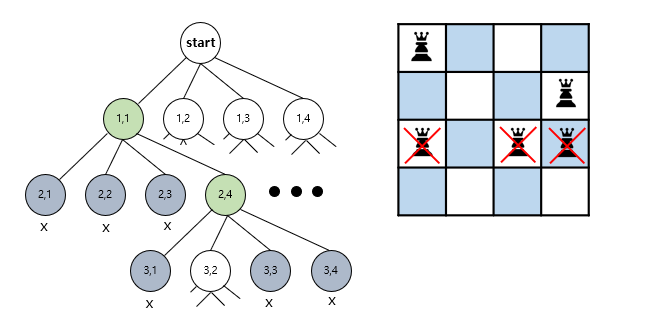
위 그림은 보면 3행의 (3,1),(3,3),(3,4) 에는 퀸을 배치 할 수 없다. 따라서 이 경로를 더 이상 탐색하지 않고 (3,2)를 선택한다.
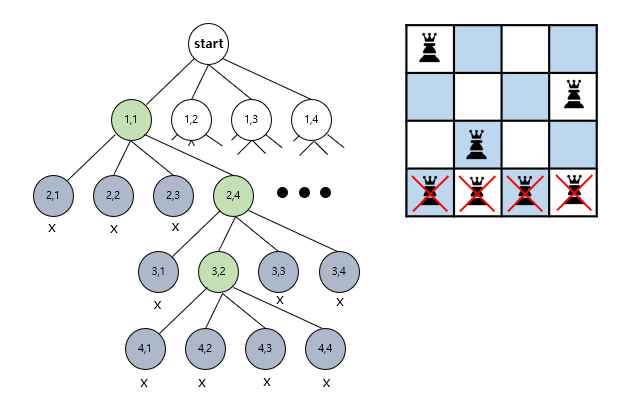
위 그림을 보면 4행에 어디에도 퀸을 배치할 수 없다. 이 때 (1,1)을 선택했을 경우 어떤 경우에도 퀸을 배치 할 수 없다는 것을 확인했다. 그렇기에 1행으로 돌아가 (1,2)를 선택한 후 다시 탐색을 진행한다.
위와 같은 방식으로 노드를 탐색, 가지치기를 진행하며 탐색하면 다음과 같은 결과를 얻을 수 있다.
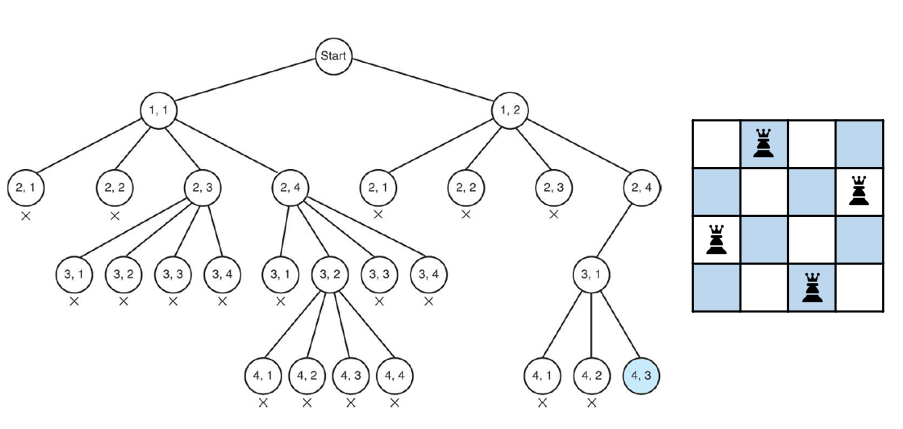
이렇게 백 트래킹을 이용해서 N-Queen문제를 해결하면, 단순 DFS 방식보다 훨씬 효율적으로 답을 구할 수 있다.
구현
Java
처음에는 NxN 크기의 체스판에 퀸을 배치하기에 2차원 배열이 필요할 것이라 생각했다.
하지만 N-Queen 문제는 무조건 한 행에 하나의 퀸을 배치하기 때문에 다음과 같이 퀸의 위치를 나타낼 수 있다.
col[1] = 2; //1행 2열에 위치
col[2] = 4; //2행 4열에 위치
col[3] = 1; //3행 1열에 위치
col[4] = 4; //4행 4열에 위치구현
import java.io.*;
public class Main {
static int N;
static int[] chess;
static int count=0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
chess = new int[N];
n_Queen(0);//시작 열
System.out.println(count);
}
public static void n_Queen(int depth){
//모든 퀸을 배치했다면
if(depth == N){
count++;
return;
}
for(int i=0;i<N;i++){
chess[depth]=i;
if(check(depth)){
n_Queen(depth+1);
}
}
}
public static boolean check(int col){
for(int i=0;i<col;i++){
//해당 열의 행과 i열의 행 비교 (같은 행에 존재하는지)
if(chess[col] == chess[i])
return false;
//열 끼리의 차와 행 끼리의 차가 같은 경우 (대각선 상에 존재하는지)
else if(Math.abs(col-i) == Math.abs(chess[col]-chess[i]))
return false;
}
return true;
}
}