문제
두 요소의 합이 target이 되는 numbers의 요소 index를 구하자
1 ≤ index1 < index2 < numbers.length
입력
- 오름차순으로 정렬되어 있는 정수 배열 numbers
- 정수 target
출력
- [index1, index2] → 합이 target이 되는 numbers의 요소 인덱스 배열 (길이 2)
나의 풀이
접근
일단 입력으로 받는 정수 배열 numbers가 오름차순으로 정렬되어 있다는 것에 주목해보자.
합이 target이 되는 요소 “2개” 만 찾으면 되니, 사실상 바로 Two Pointers 가 떠올랐다.
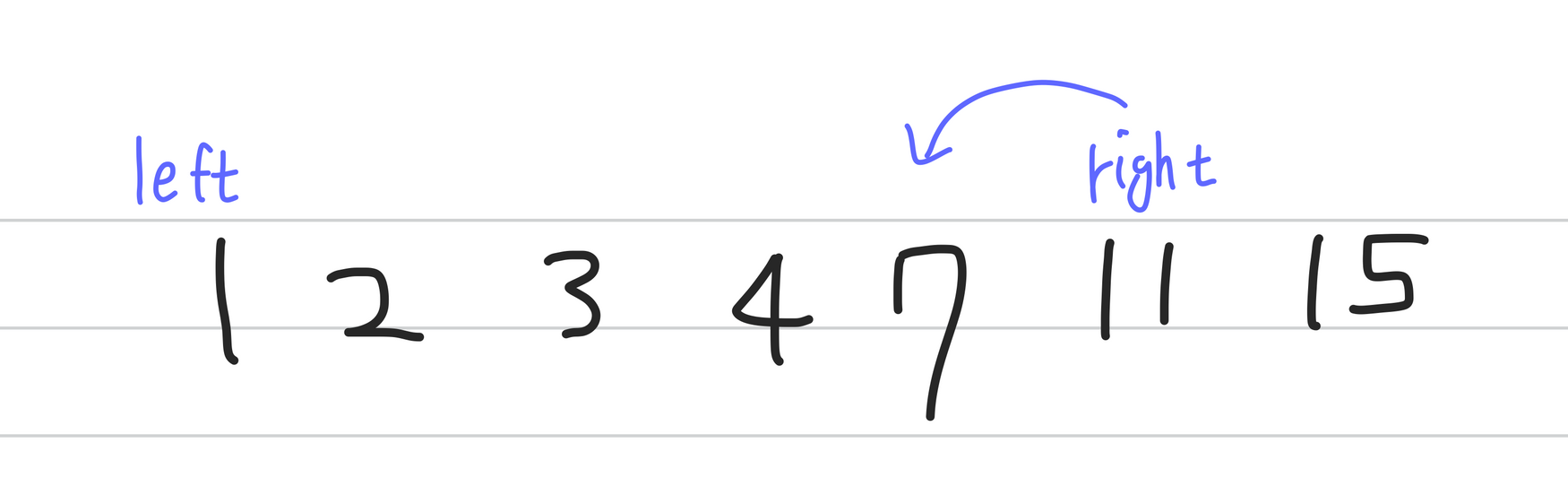
위와 같이 left와 right 포인터를 이용해 동시에 두 요소를 탐색하며 합을 검사한다.
위 사진은 numbers[left] + numbers[right] 가 target보다 값이 크므로, numbers가 오름차순으로 정렬되어 있는 것을 이용해, right 값을 1 감소시킨다.

위 사진은 numbers[left] + numbers[right] 가 target보다 값이 작으므로, numbers가 오름차순으로 정렬되어 있는 것을 이용해, left를 1 증가시킨다.
따라서 아래와 같이 구현했다.
구현 코드
class Solution:
def twoSum(self, nums, target):
left, right = 0, len(nums) - 1
while left < right:
if nums[left] + nums[right] > target:
right -= 1
elif nums[left] + nums[right] < target:
left += 1
else:
return [left+1, right+1]결과

Time: O(n)
Space: O(1)
다른 풀이
def twoSum(self, numbers, target):
dic = {}
for i, num in enumerate(numbers):
if target - num in dic:
return [dic[target-num]+1, i+1]
dic[num] = i
위 풀이는 아래와 같이 numbers에 있는 값과 index를 dictionary에 하나씩 넣는 방식을 이용한다.
- numbers에 있는 요소와 index를 키, 값으로 하나씩 순서대로 넣는다.
- 만약 target - num의 값이 dic 안에 있다면
- 해당 dic[target-num] +1, i + 1 을 return 한다
해당 풀이도 O(n)의 시간 복잡도를 가지고 있다.
사실 if target - num in dic: 이 구문에서 O(n)의 시간 복잡도를 또 가질 줄 알았는데, dictionary 자료형은 해시 맵의 구조를 사용하기 때문에, in 연산자를 사용하여 키 존재를 확인하는 것은 평균적인 상수 시간 O(1) 작업이라고 한다.
하지만 만약 dic의 자료구조가 list라면 O(n)의 시간복잡도를 가지니 주의해야겠다.