209. Minimum Size Subarray Sum

문제 링크: https://leetcode.com/problems/minimum-size-subarray-sum/

문제

nums 배열에서 총합이 target 이상이면서 그 중 길이가 최소인 SubArray를 찾는다.

입력

• 양수로만 이루어진 정수 배열 nums
• 양수 정수 target

출력

• SubArray 길이

---

나의 풀이

여러 가지 방안을 생각해보다가, 도저히 좋은 아이디어가 떠오르지 않아서 결국 무식한 방법을 써보기로 했다.

Sliding Window 기법을 사용해 모든 경우를 다 탐색하는 방법을 선택했다.

시도

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int right, sum;
        int answer = 1000000;
        for (int num : nums) {
            if (num >= target)
                return 1;
        }

        for (int left = 0; left < nums.length - 1; left++) {
            sum = nums[left];
            right = left;
            while (right < nums.length -1) {
                sum += nums[right+1];
                right++;
                if (target <= sum) {
                    answer = Math.min(right - left + 1, answer);
                }
            }
        }

        return answer == 1000000 ? 0 : answer;
    }
}

• 먼저, target보다 크거나 같은 요소가 있는 지 먼저 계산하고, 있다면 1을 return하도록 했다. → O(n)
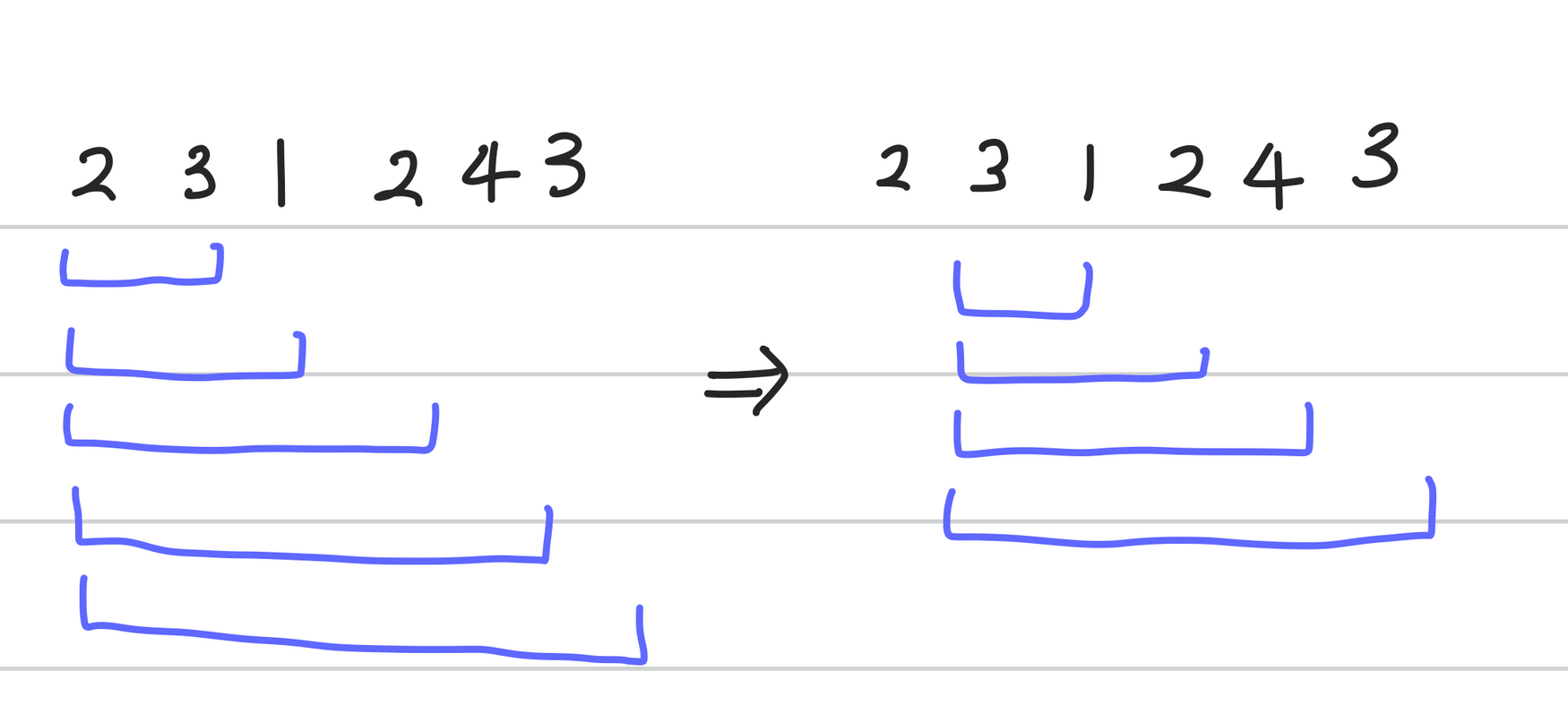
• 그리고 window의 시작점을 오른쪽으로 한 칸씩 옮겨가며 모든 경우의 수를 계산 → O(n^2)
  • 그 window의 크기 또한 한 칸씩 늘리며, window 안에 있는 요소의 합을 구한 후 만약 target 보다 크거나 같다면, answer와 비교해 최소값을 answer에 할당한다.
• 만약 answer가 초기값 그대로라면 0을, 아니라면 answer를 return 한다.

아래 사진과 같은 방식으로 진행되는 코드이다.

결과

하지만 18번째 케이스에서 시간초과가 발생해 실패했다..!

---

다른 풀이

public int minSubArrayLen(int target, int[] nums) {
        int sum = 0, from = 0, win = Integer.MAX_VALUE;
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            while (sum >= target) {
                win = Math.min(win, i - from + 1);
                sum -= nums[from++];
            }
        }
        return (win == Integer.MAX_VALUE) ? 0 : win;
    }

• 먼저, sum에 nums의 첫번째 요소부터 더해나간다.
  • 만약, sum이 target보다 크거나 같게 된다면, sum이 target보다 작아질 때까지 sum에서 처음 요소 값부터 차례대로 뺀다. 이 과정에서 win의 값도 계속 업데이트
    

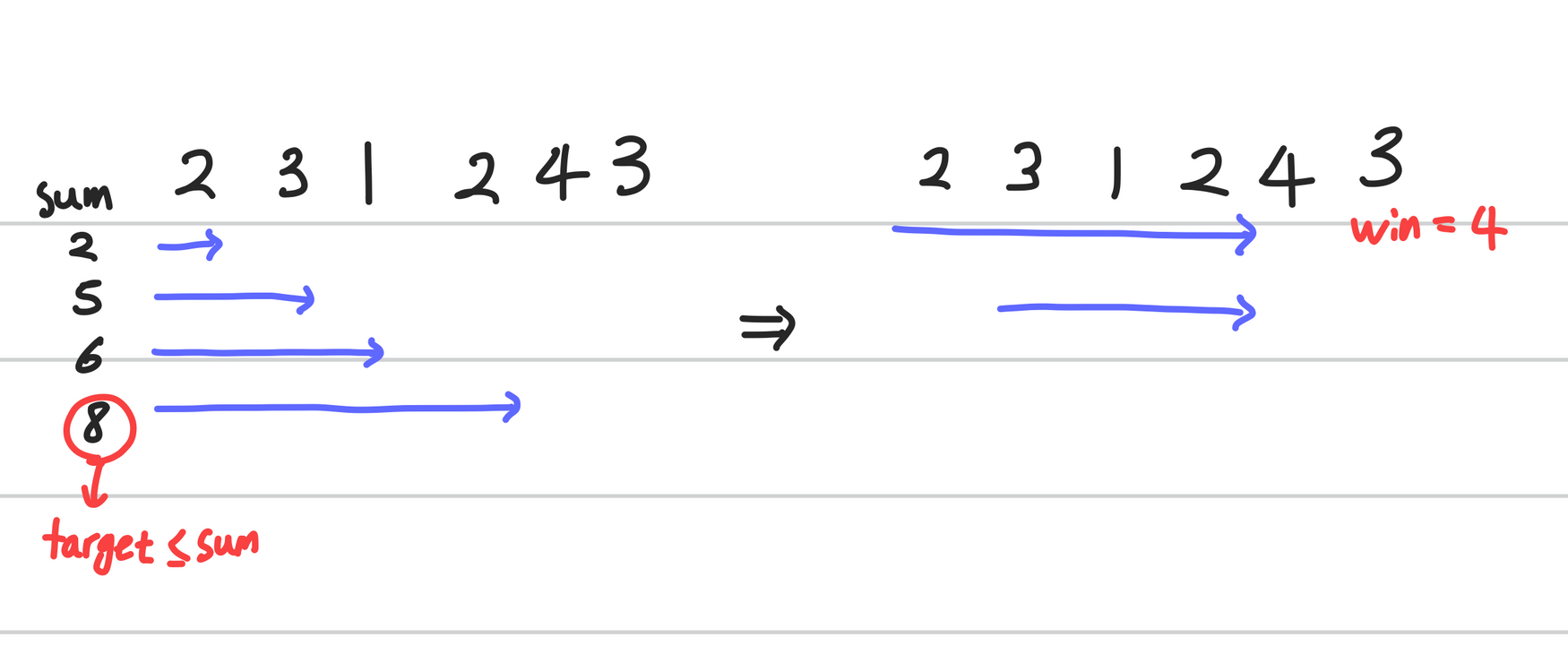
i = 3일 때의 과정을 그림으로 나타내면 아래와 같다.

2 + 3 + 1 + 2 까지 더했을 때, sum이 8이 되므로 sum ≥ target 조건에 성립되어, while문으로 실행하게 된다.

오른쪽 그림처럼 while문을 실행하는데, 첫 번째 요소 값을 빼면 바로 sum ≥ target 조건에 성립되지 않아,while문을 빠져나오게 된다.

나와 비슷하면서도 다른 점은 window의 크기를 자유자재로 바꾸면서 탐색했다는 점이다.

위의 그림에서도 보면, while문에서 sum의 값이 target보다 작아지자, 그 window를 유지한채 다음 요소까지 window 크기를 늘려가며 탐색했다는 것이다.

내 풀이 같은 경우는 어찌보면 계속 중복해서 계산하는 구간이 너무 많았지만, 이 풀이를 이용하면 계산했던 구간은 다시 재사용한다는 점으로, 시간복잡도를 O(n)으로 감소시켰다.

이런 부분합에 관련된 문제는 항상 직접적으로 구한다기 보다, 부분합의 부분합을 이용하거나, 아니면 전체에서 감소시켜가며, 부분합을 찾는 아이디어가 대부분인 것 같다.

이번 문제에서는 아무래도 부분합 “최대”를 찾아야 하는 문제이므로, 전체의 합에서 감소시켜나가는 아이디어가 문제의 핵심이었다고 생각한다.