프로그래머스 알고리즘 문제 최대공약수와 최소공배수

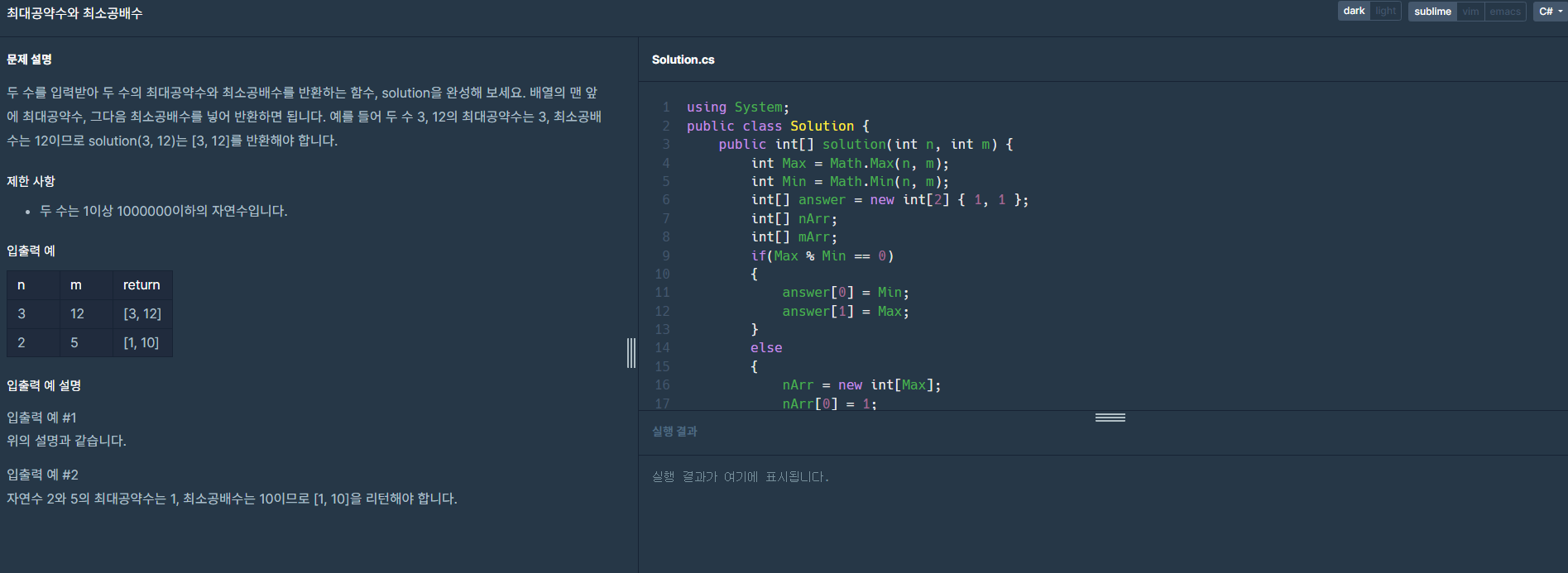
문제를 풀기 위해 최대 공약수와 최소 공배수가 무엇인지 어떻게 구하는지 알아보자

1. 최대 공약수

최대공약수는 공용되는 약수의 최대를 나타낸다.
예시로 4와 12가 있다고 하면 4의 약수 1,2,4 이다. , 12의 약수 1, 2, 3, 4, 6, 12이다. 이 중 공통되는 값 1, 2, 4중에서 가장 큰 값인 4가 최대 공약수가 되는 것이다.

2. 최소 공배수

최소 공배수는 공용되는 배수의 최소를 나타낸다.
예시로 4, 6이 있다고 하면 4의 배수 4, 8, 12, 16, 20...이며 6의 배수 6, 12, 18, 24...이다. 이중에서 가장 작은 값인 12이다.

3. 간단하게 풀자(최대 공약수)

n과 m의 최대 공약수를 컴퓨터로 구할려면 for문으로 돌려서 (1~n값 까지)비교하여 해당 값을 저장해야 된다.

int n = 4;
int m = 12;
List<int> nArr = new List<int>();
List<int> mArr = new List<int>();
int[] answer = new int[2];
for(int i = 1; i <= n; i++)
{
	if(n % i == 0)
    	nArr.Add(i);
}
for(int i = 1; i <= m; i++)
{
	if(m % i == 0)
    	mArr.Add(i);
}

nArr에는 1, 2, 4가 들어있고 mArr에는 1, 2, 3, 4, 6, 12가 들어있다.
약수까지는 쉽게 구했다

값이 크고 약수가 많을 수록 비교해야 되는 것들이 많아진다. for문으로 1~n까지 돌려서 2개값이 같은지 비교해봐야 된다.

for(int i = 1; i <= (n < m ? n : m); i++)
{
	if(nArr.Contains(i) && mArr.Contains(i))
    {
    	answer[0] = i;
    }
}

이렇게 하면 answer[0]에 최소 공배수 4가 저장된다.

4. 간단하게 풀자(최소 공배수)

n과 m의 최소 공배수를 컴퓨터로 구할려면 for문으로 돌려서 (큰 값 ~ n * m값 까지)비교하여 해당 값을 저장해야 된다.

int n = 4;
int m = 12;
List<int> nArr = new List<int>();
List<int> mArr = new List<int>();
int[] answer = new int[2] {1,1};
int max = Math.Max(n,m);
int min = Math.Min(n,m);
int nCount;
int mCount;
for(int i = 2; n != 1; i++)
{
	int nCount = 0;
	while(n % i == 0)
    {
    	n /= i;
        nCount++;
    }
    nArr.Add(i, nCount);
}
for(int i = 2; m != 1; i++)
{
	int mCount = 0;
	while(m % i == 0)
    {
    	m /= i;
        mCount++;
    }
    mArr.Add(i, mCount);
}

어렵게 최소 공배수, 최소 공배수 풀기

하지만 이렇게되면 값이 클 때 시간이 오래 걸릴 수 있다 그렇기에 수학적으로 풀어볼려고 한다.
위처럼 n = 4이고 m = 12일때 4의 약수는 2^2 이다 12의 약수는 2^2 , 3이다
이 중에서 겹치는 값 2^2가 최소 공배수이며 2^2 * 3가 최대 공약수 이다.
이를 구하기 위해서는 위처럼 for문으로 1 ~ n까지 돌려 같은지 확인해야 한다.

int n = 6;
int m = 10;
int max = Math.Max(n, m);
int min = Math.Min(n, m);
int fixedMax = max;
int fixedMin = min;

int[] answer = new int[2] { 1, 1 };
Dictionary<int, int> minArr = new Dictionary<int, int>();
Dictionary<int, int> maxArr = new Dictionary<int, int>();
minArr.Add(1, 1);
maxArr.Add(1, 1);
if (max % min == 0)
{
    answer[0] = min;
    answer[1] = max;
}
else
{
    for (int i = 2; i <= fixedMax; i++)
    {
        int minCount = 0;
        int maxCount = 0;
        while (max % i == 0)
        {
            max /= i;
            maxCount++;
        }
        while (min % i == 0)
        {
            min /= i;
            minCount++;
        }
        if (maxCount > 0) { maxArr.Add(i, maxCount); }
        if (minCount > 0) { minArr.Add(i, minCount); }
    }
    foreach (KeyValuePair<int, int> i in maxArr)
    {
        if (minArr.TryGetValue(i.Key, out n))
            answer[1] *= (int)Math.Pow(i.Key, Math.Max(n, i.Value));
        else
            answer[1] *= (int)Math.Pow(i.Key, i.Value);
    }
    foreach (KeyValuePair<int, int> i in minArr)
    {
        if (maxArr.TryGetValue(i.Key, out n))
            answer[0] *= (int)Math.Pow(i.Key, Math.Min(n, i.Value));
        else
            answer[1] *= (int)Math.Pow(i.Key, i.Value);
    }
}
Console.WriteLine("최대 공약수 : {0} , 최소 공배수 : {1}", answer[0], answer[1]);

처음에는 int형 배열을 n,m 두개를 만들고 값의 크기 만큼 갯수를 할당하여 약수의 값 - 1의 인덱스에 갯수를 넣었다. 하지만 이는 용량도 많이 차지하면서 속도도 매우 느려서 구현을 포기했다.

두번째는 List, Queue <int[]>을 2개 만들어 비교하는 방법
이 방법은 .contains를 사용해 값이있는지 확인하여 비교하면 되서 첫번째꺼랑 현재 작성한것이랑 비슷한 속도를 낸다.

이렇게 만들면 더욱 복잡하고 for과 while문을 많이 쓴다. 그러면서 최악일때 시간복잡도는 전의 코드보다 별로다.
수학적 접근을 잘 활용하면 보다 깔끔하고 시간 복잡도가 작은 것을 만들 수 있지만 이 처럼 더욱 괴상해질 수도 있다.
(단순하게 필자가 코딩을 못해서 그럴수도 있다. 만약 이보다 깔끔한 방법을 알고있으면 알려주세요 수정하겠습니다.)