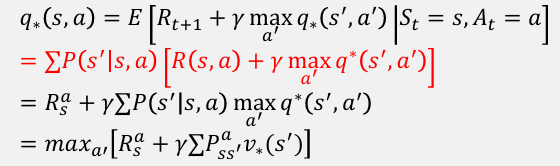Bellman Equation
Retrun and State Value Function
Retrun G: 한 에피소드의 reward(보상)
State value function V(S): 주어진 상황의 상태 에서 측정되는 reward이다.
Bellman equation
동적 프로그래밍 (dynamic programming)과 강화학습의 기본적인 개념이다.
특정 policy를 따르는 동안 상태의 값(value)와 그 상태로부터 얻을 수 있는 기대 누적 보상(return) 사이의 관계를 표현한다.
Dynamic Programming
Richard Bellman이 제안한 것으로 Bellman을 코드로 나타낸 것이다. 복잡한 문제를 단순한 문제와 작은 문제로 구분하여 재귀적으로 해결하는 문제 해결 기법이다.
예시) 피보나치 수열
Bellman Expectation Equation
Bellman Expectation Equation은 policy에 따른 상태의 값을 예상되는 즉각적인 보상과 다음 상태들의 기대값으로 표현한다.
For state-value function
In MRP model

In MDP model

Action-Value Function
에이전트 𝜋가 상태 에 대한 작업 을 선택할 때의 평균을 반환한다. 정책 𝜋에 따른 구체적인 action이 얼마나 좋은지 추정한다. 이것들 Q-value 라고 부른다.
Notation: or
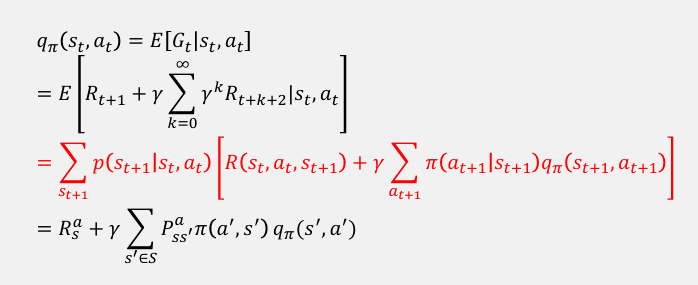
Bellman Optimality Equation
• 벨만 방정식은 모든 policy 𝝅에 대한 상태 값을 계산하는 방법을 보여준다.
• Bellman Optimality Equalies는 최적의 policy 𝝅에 초점을 맞춘다.
optimal State-Value Function
최적의 policy에 따른 상태의 값은 상태로부터 최상의 조치에 대한 기대 수익과 같아야 한다는 사실을 표현한다.
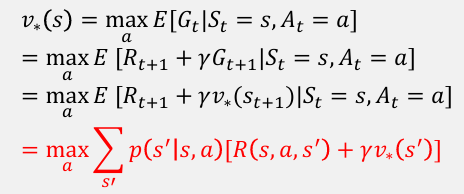
Optimal Action-Value Function