Markov Decision Process
Markov Property
미래의 사건은 현재의 상태만으로 예측 가능하다.
시간에 따른 확률적 상태 전이를 나타내는 수학적 모델이다. 다음과 같이 수식으로 나타낼 수 있다.
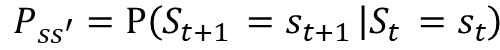
은 미래이고 는 현재를 나타낸다.
MP ≡ <𝑆, 𝑃>
- S : State space =
- P: Transition probability model (matrix)
Python Example
import numpy as np
import copy
def mp(p, day):
p2 =copy.deepcopy(p)
if day<1:
print("error")
return 0
elif day==1:
return p
else:
for i in range(day):
p2 = np.matmul(p, p2)
return p2
# main
p= [[0.25, 0.75], [0.4, 0.6]]
mp(p, 3)Markov Reward Process
MP에 reward R과 discount factor 𝛾을 더한 수학적 모델
MRP ≡ <𝑆,𝑃,𝑅,𝛾>
- R: Reward
- 시간 t에서 상태 S에 있을 때 시간 t+1에서 기대되는 보상
- 즉각적인 보상
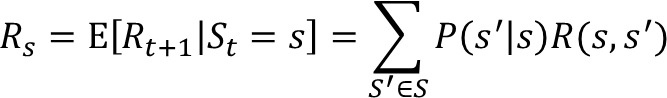
- 𝛾: Discount Factor
- return값이 무한대로 빠지는 것을 방지하기 위해 사용된다.
- discount factor가 작으면 return이 현재 보상에 초점을 맞추고 discount factor가 크면 먼 미래의 보상에 초점을 맞춘다.
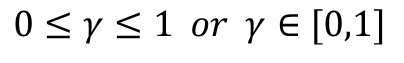
-
Episode
- 시작 상태에서 종료 상태까지의 한 시리즈를 에피소드라고 한다.
-
Return (누적합)
- episode에서 reward의 합
- state transition probability와 상관없고 회차가 주어지면 state transition probability은 항상 1.0이다.
- 수식은 다음과 같다.
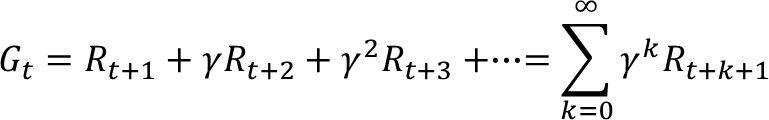
Reward Python Example
import numpy as np
#reward matrix
R =[[0, 2, 0, 0, 1, 0],
[0, 0, -2, 0, 1, 0],
[0, 0, 0,100, 2, 5],
[0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, -3, 0],
[1, 0, 0, 0, 0,-10]]
# episode generator
episode =[]
episode.append(0)
done =True
inx=0
while(done):
state = rnd_state(episode[inx])
episode.append(state)
inx=inx+1
# print(state)
if state==3:
done=False
print(episode)
#state selector
def rnd_state(n):
epi =0
if n==0:
epi =np.random.choice([1,4], size=1)[0]
elif n==1:
epi =np.random.choice([2,4], size=1)[0]
elif n==2:
epi =np.random.choice([3,4,5], size=1)[0]
elif n==4:
epi =np.random.choice([1,4], size=1)[0]
elif n==5:
epi =np.random.choice([0,5], size=1)[0]
else:
epi =3
print("error")
return epi
#Calculate Return G
G =0
gamma =0.5
for i in range(1,len(episode)):
G =G +(gamma**(i-1) *R[int(episode[i-1])][int(episode[i])])
print(f'ReturnG: {G}')Markov Decision Process
MRP에 에이전트의 액션 A가 추가된 모델이다. MP나 MRP 모델의 상태 전이는 시간별 상태 전이 확률에 의해 자동으로 수행된다.
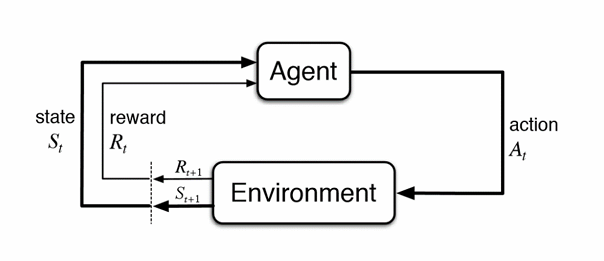
- Notation
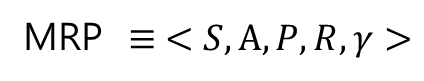
A는 action의 집합으로 예를 들면 A={Go, Back, Jump, Attack, ...}으로 나타낼 수 있다.
- policy ()
agent는 policy에 따라 상태 에서 액션 를 결정한다.
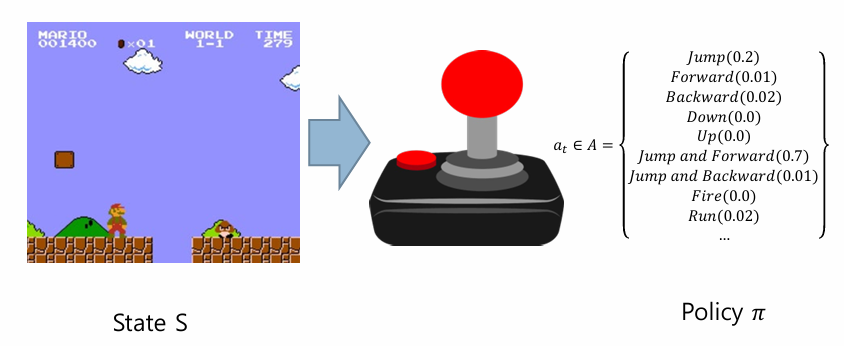
위의 그림과 같이 에서 로 갈 때 모든 액션들을 통합하여 policy 라고 한다.
State Transition probability in MDP
State Transition probability and reward considering policy
Deterministic Environment
episode가 정해져 있는 환경으로 무작위성이 없고 상황 S에서 S'로의 확률이 1 또는 0이다. 예를 들면, 게임과 같은 상황이다.
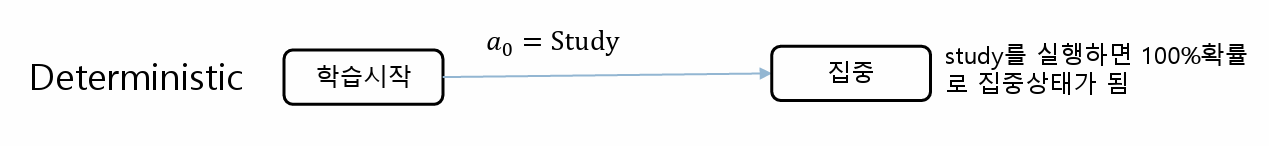
Stochastic Environment
무작위성이 포함되어 있으며, 동일한 action에 대해 여러 상태가 발생할 수 있다. 즉, 확실하게 결정이 되지 않은 상태이다. 우리의 일상생활을 예로 들 수 있다.

