BOJ 1002 터렛

김재섭·2021년 3월 23일

1002 BOJ 1002 백준 백준 1002 알고리즘 터렛

백준

목록 보기

1/10

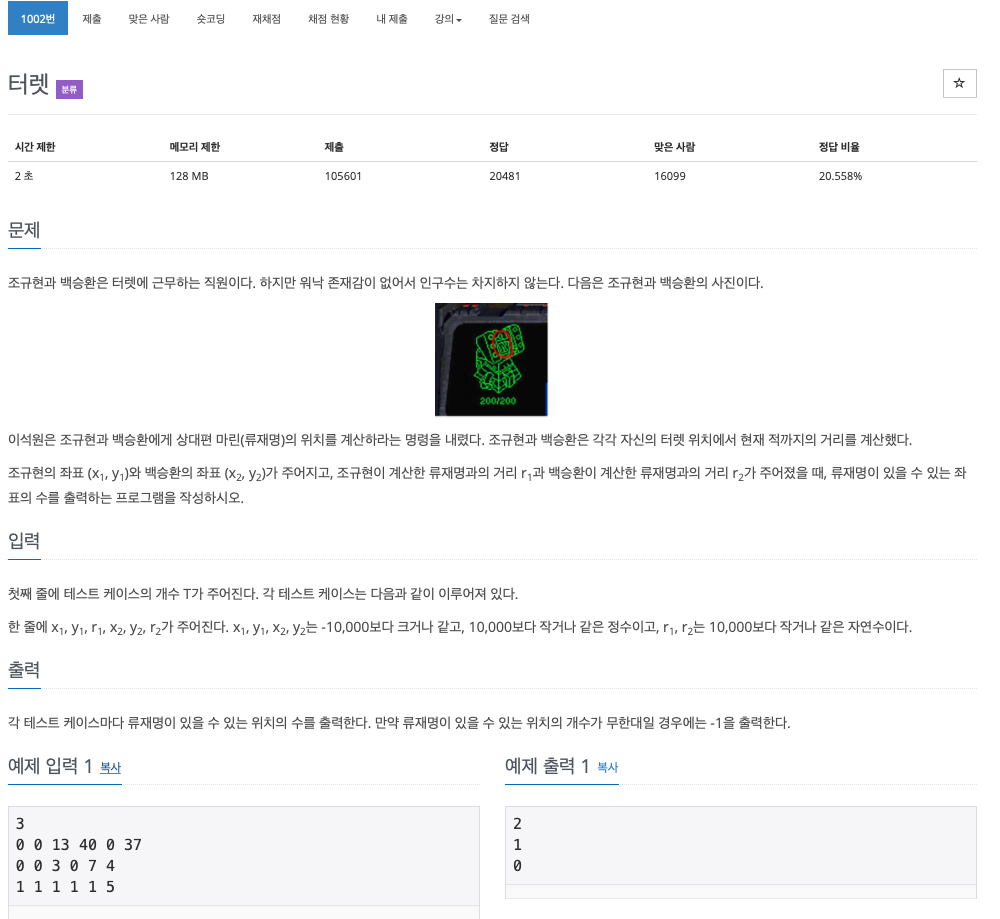
문제

https://www.acmicpc.net/problem/1002

아이디어

문제를 봤을 때 좌표 상에 두 점을 찍고 반지름을 가지고 원을 그려봤을 때 접하는 점을 출력하면 되겠다고 생각했지만 수학 상식의 부족으로 구현하지 못했다.

초기 아이디어

두 원을 배열 상에 그린다. (배열의 원 내부의 모든 좌표에 +1을 해준다.)
겹치는 부분은 2가 되기 때문에 좌표를 추려낸다

틀린 아이디어였다. 원의 내부까지 모두 색칠하면, 거리가 13이 아닌 점들도 포함된다.

두 번째 아이디어

원의 내부는 색칠하지 말고 원주에 색칠해서 겹치는 점만 추려낸다.

이 아이디어는 가능 할 것 같지만 인덱스 제어가 어렵고, 문득 두 원의 외적, 내적, 두 점이 겹치는 경우를 추려내는 수학 공식이 있던 것이 생각나서 검색했다.

세 번째 아이디어

https://mathbang.net/101

위 링크에서 수학 공식을 찾고, 여러 블로그에서 코드를 찾아봤다.

여러 코드를 보다보면 두 원간의 거리인 d를 구할 때 맨하탄 거리 공식이 아닌 유클리드 거리 공식을 사용하는데,

별 이유 없이 맨하탄 거리를 자주 사용했기 때문에 차이를 알 수 없어서 다시 이유를 찾아 나섰다.

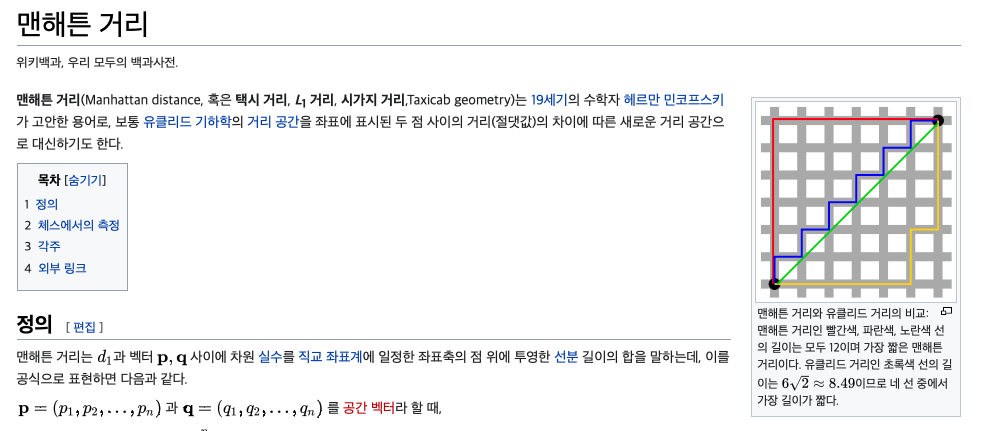
https://ko.wikipedia.org/wiki/맨해튼_거리

위 이미지를 보면 우리가 필요한 거리는 초록색 선인데 맨하탄 거리는 단지 좌표 간의 차이를 거리로 두기 때문에 빨간, 파란, 노란색 선이 되는 것이다. 때문에 피타고라스 공식으로 나머지 선분의 길이를 구하듯 유클리드 거리 공식을 통해 d를 계산한다.

코드

#include <iostream>
#include <cmath>

using namespace std;

int T;
int x[2], y[2], r[2];
double d;

int main(void)
{
    //freopen("input_1.txt", "r", stdin);

    cin >> T;

    while (T--) {
        cin >> x[0] >> y[0] >> r[0] >> x[1] >> y[1] >> r[1];

        if (x[0] == x[1] && y[0] == y[1]) {
            if (r[0] == r[1])
                cout << -1 << endl; // 원이 완전히 겹침
            else
                cout << 0 << endl; // 큰 원 안에 작은 원이 있고 반지름이 다름

            continue;
        }   

        d = sqrt((x[1]-x[0]) * (x[1]-x[0]) + (y[1]-y[0]) * (y[1]-y[0]));

        if (d == abs(r[1]-r[0]) || d == (r[1]+r[0])) { // 한 점에서 겹치는 경우
            cout << 1 << endl;
            continue;
        }   

        if (r[0]+r[1] < d || d < abs(r[1]-r[0])) { // 원이 완전히 떨어진 경우, 큰 원 안에 작은 원이 있는 경우
            cout << 0 << endl;
            continue;
        }   

        if (abs(r[1]-r[0]) < d && d < (r[1]+r[0])) { // 두 원이 두 점에서 겹치는 경우
            cout << 2 << endl;
            continue;
        }   
    }   

    return 0;
}