Asymmetric key cryptography

🔎 대칭키 암호학 (Symmetric key cryptography): 송신자와 수신자 사이 비밀 키 공유
→ 키의 관리와 분배 어려움

---

🔎 비대칭키 암호학 (Asymmetric key cryptography)

= 공개키 암호학 (public key cryptography)

• 송신자와 수신자 사이 비밀 키를 공유하지 않음
• 공개키-개인키 쌍 사용
  공개키: 모두 다 알고 있음
  비밀키: 본인만 알고 있음
• 많은 연산 필요. 속도 느림
  

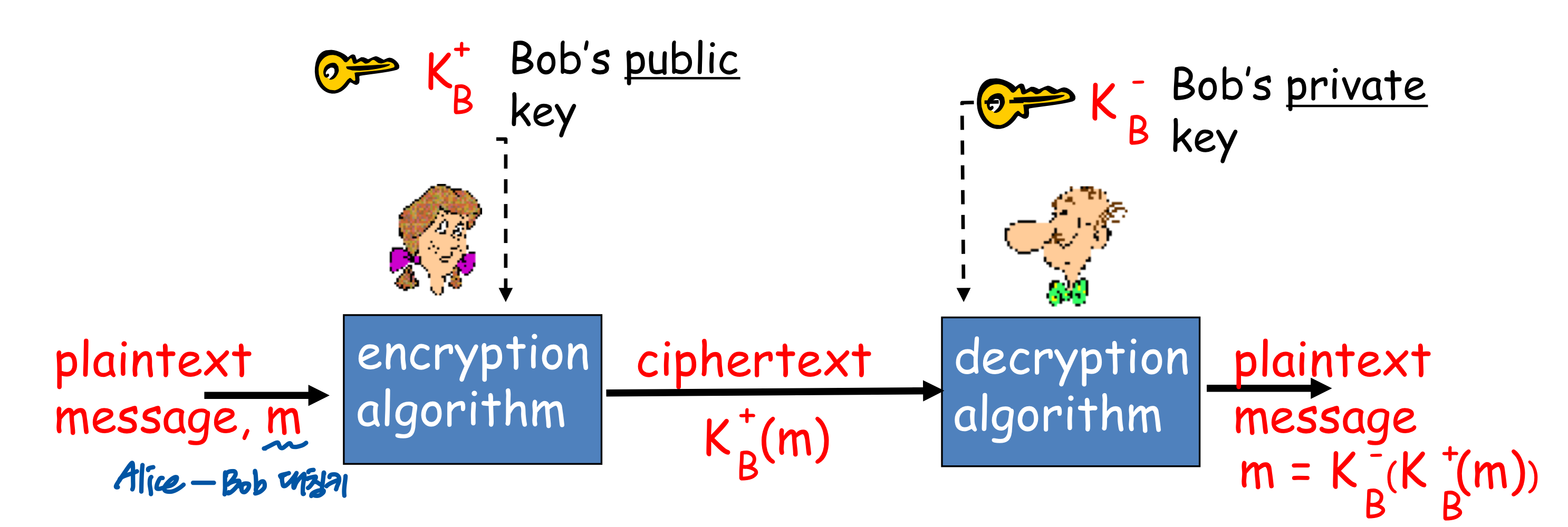
➡️ 암호화

📤 송신자 Alice: Bob의 공개키로 암호화하여 메세지 전달
📥 수신자 Bob: Bob의 개인키로 복호화하여 메세지 확인 오직 Bob만이 메세지를 복호화 할 수 있음

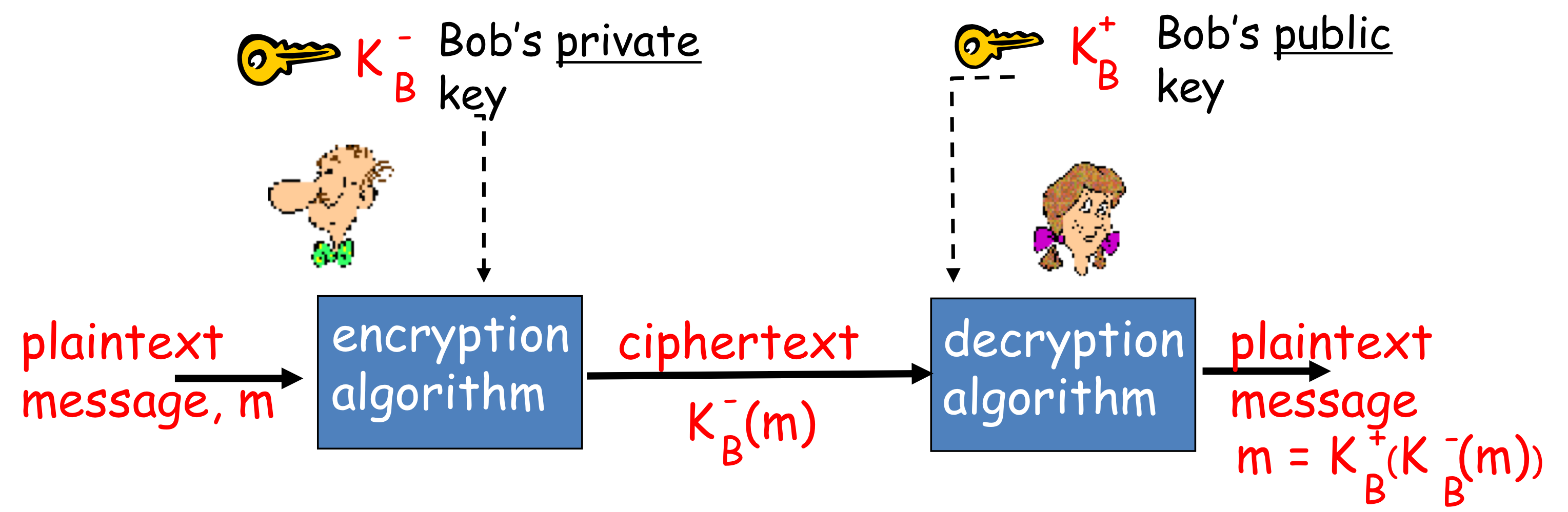
➡️ 전자서명

📤 송신자 Bob: Bob의 개인키로 암호화하여 본인이 서명했음을 증명하는 메세지 전달
📥 수신자 Alice: Bob의 공개키로 복호화하여 Bob이 서명한 메세지 확인

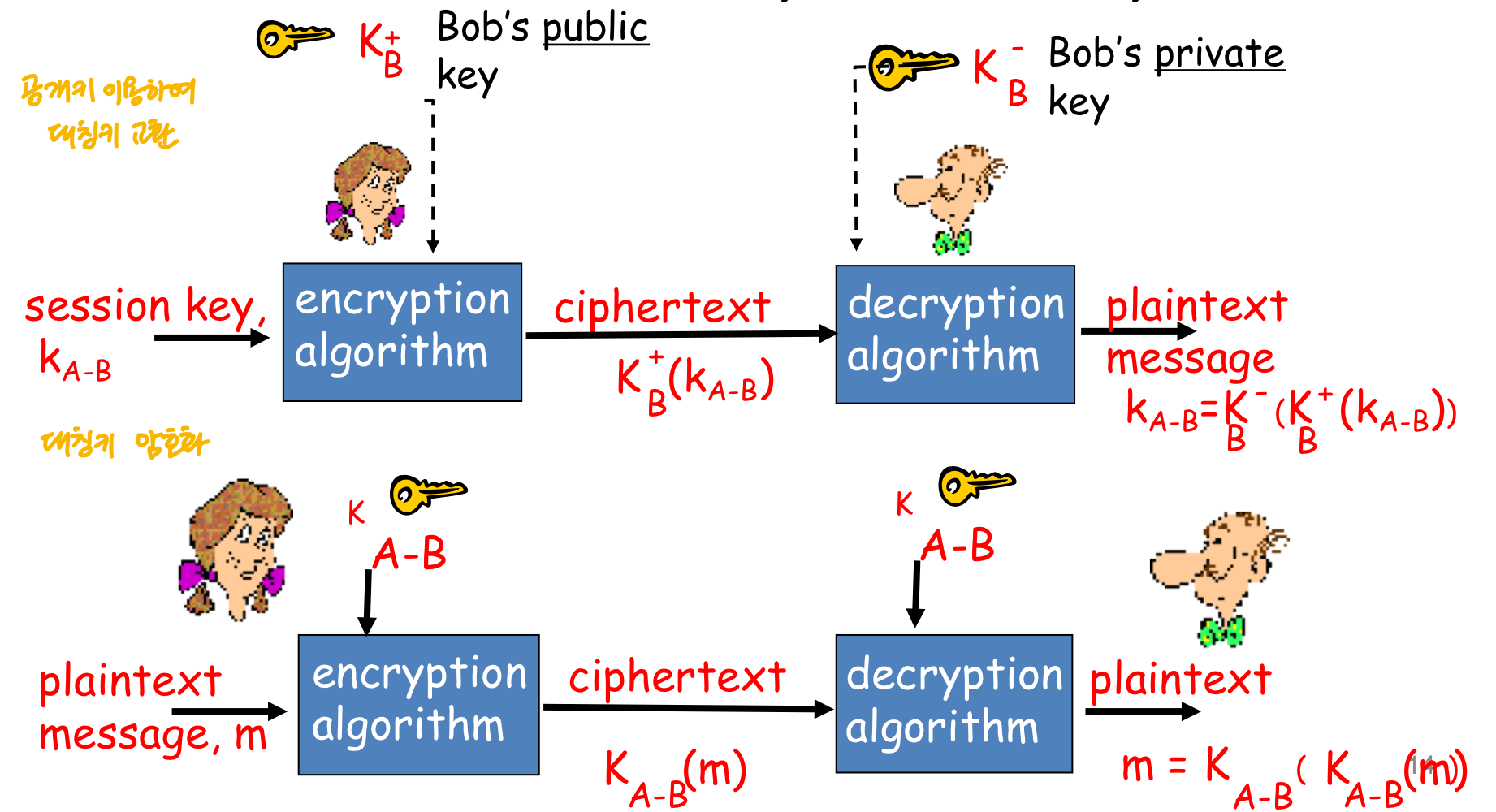
➡️ Used for establishing symmetric key

대칭키 설립에 사용

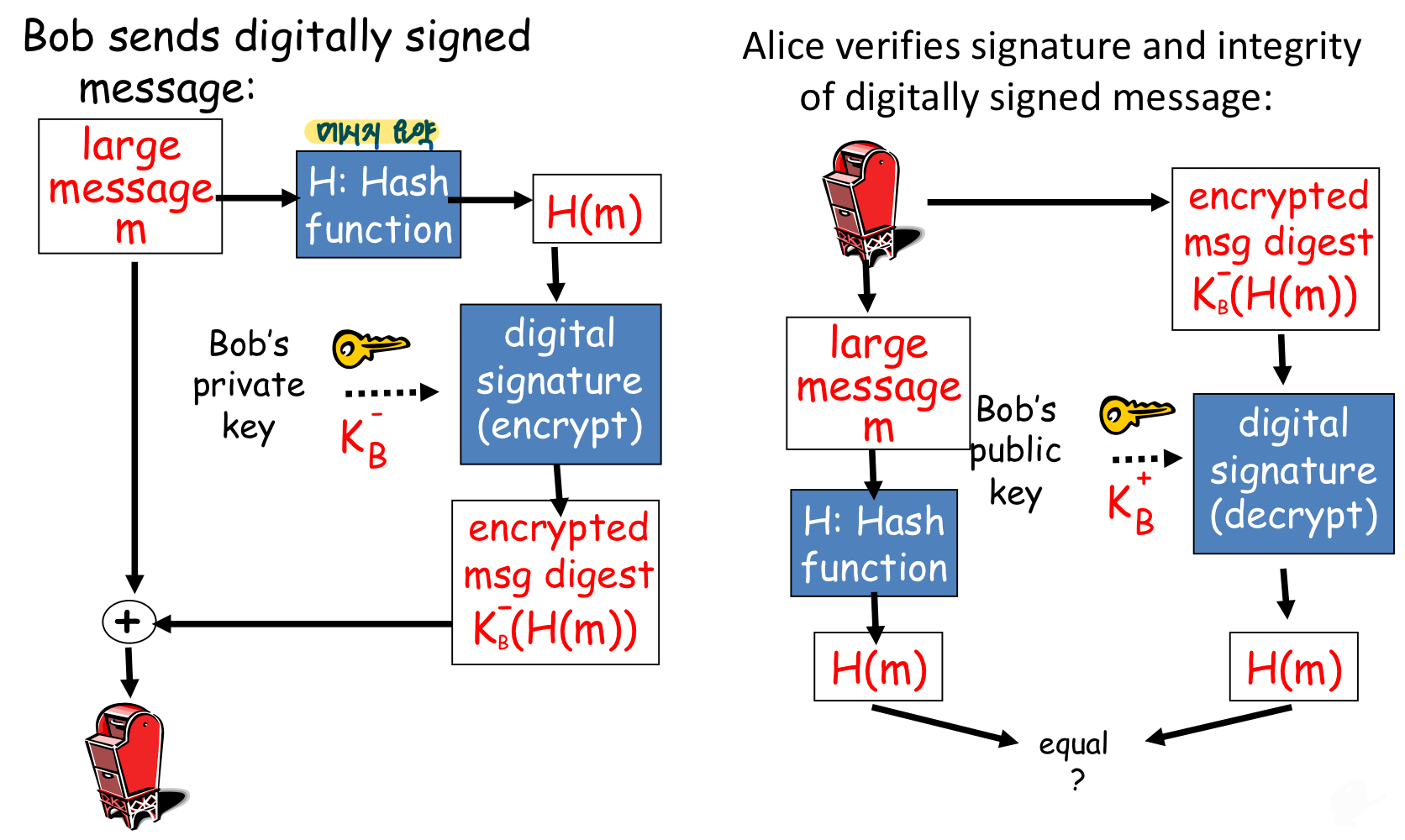
➡️ Used for signing message digest

요약한 메세지 서명에 사용

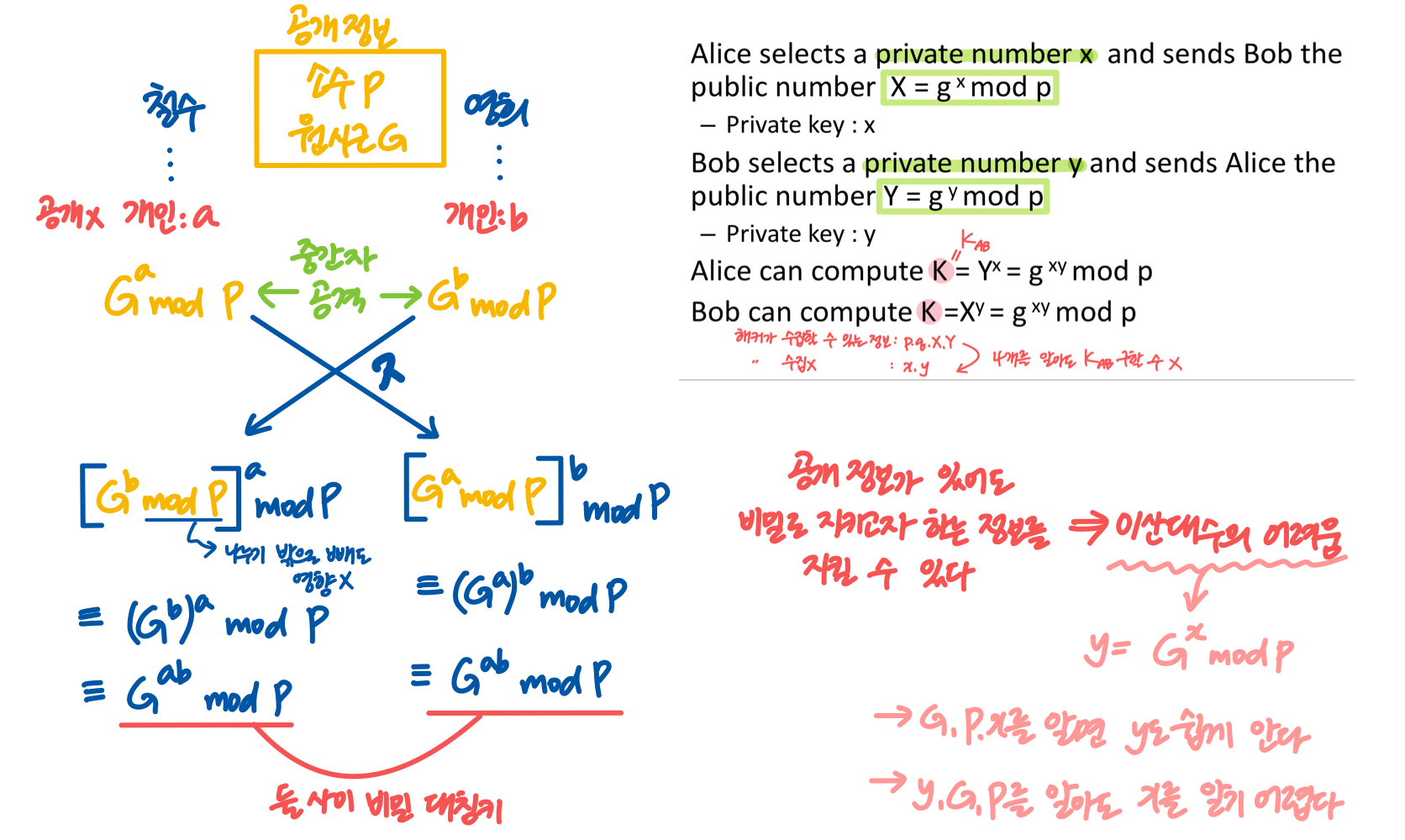
🔐 Diffie-Hellman

• 암호 이론
  → 이산로그 계산의 어려움 이용
  → 유한 필드의 지수화 쉬움 이용
• 공개키 방식을 사용하여 대칭키 공유
  (대칭키 암호화 하기 전에 diffie-hellman을 이용하여 대칭키 공유)
• 기밀성 제공
• 암호화x, 전자서명, 무결성 제공x
  ⚠️ 공개키-개인키는 오직 대칭키를 얻을 때에만 사용

❓과정
→ 송신자와 수신자 각각 개인키와 공개키 생성 후, 각자의 공개키 교환
→ 상대방의 공개키를 자신의 개인키와 합치면 비밀키 획득

1. Alice-Bob: 큰 소수 p, p보다 작은 g 생성 p,g는 공개키
2. Alice: 난수 x 생성. Bob에게 X = g^x mod p 전달 x는 개인키
   Bob: 난수 y 생성. Alice에게 Y = g^y mod p 전달 y는 개인키
3. Alice: Y^x = g^xy mod p 계산
   Bob: X^y = g^xy mod p 계산
   ➡️ Y^x = X^y Alice-Bob의 대칭키
   

🔐 RSA

• 암호 이론
  → 소인수분해 이용. 큰 수의 인수분해 어려움 이용
• 암호화o, 기밀성, 부인 봉쇄, 전자서명 제공
• 무결성 제공x

❓과정
→ 송신자가 수신자에게 공개키 요청
→ 수신자가 송신자에게 본인의 공개키 전송
→ 송신자는 전달받은 공개키를 이용하여 메세지를 암호화 후, 수신자에게 메세지 전달
→ 수신자는 개인키로 암호화된 메세지 복호화

1. 두 개의 큰 소수 p와 q 생성
2. n = p*g
   ø(n) = (p-1)(q-1) 생성
3. 랜덤으로 암호화 키 e 1<e<ø(n) 이고 ø(n)와 서로소 관계인 수 생성
4. e*d mod ø(n) = 1을 만족하는 복호화 키 d 계산
   ➡️ 공개키: P(e, n) 개인키: P(d,n)

암호화 과정

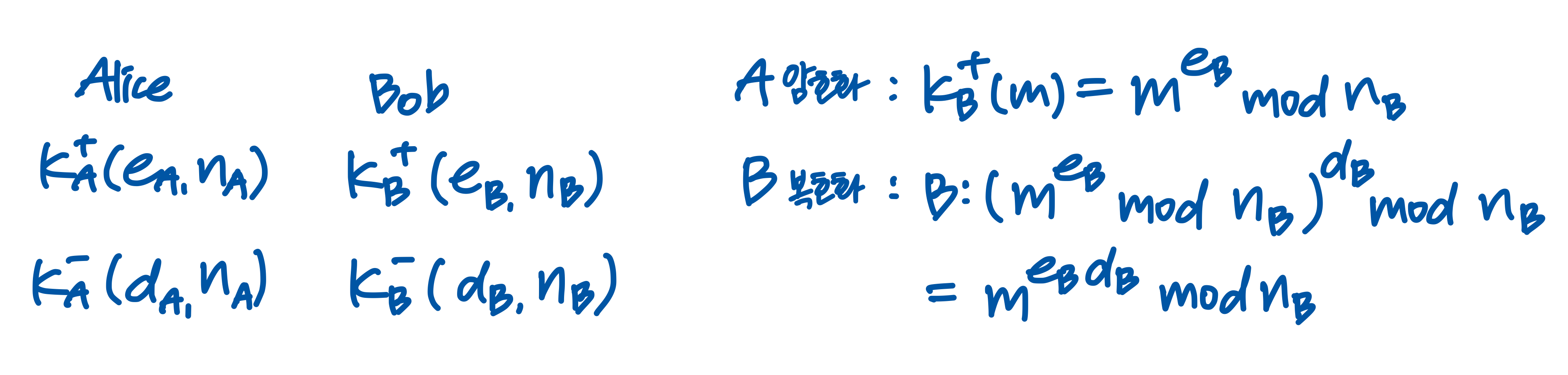
전자서명 과정

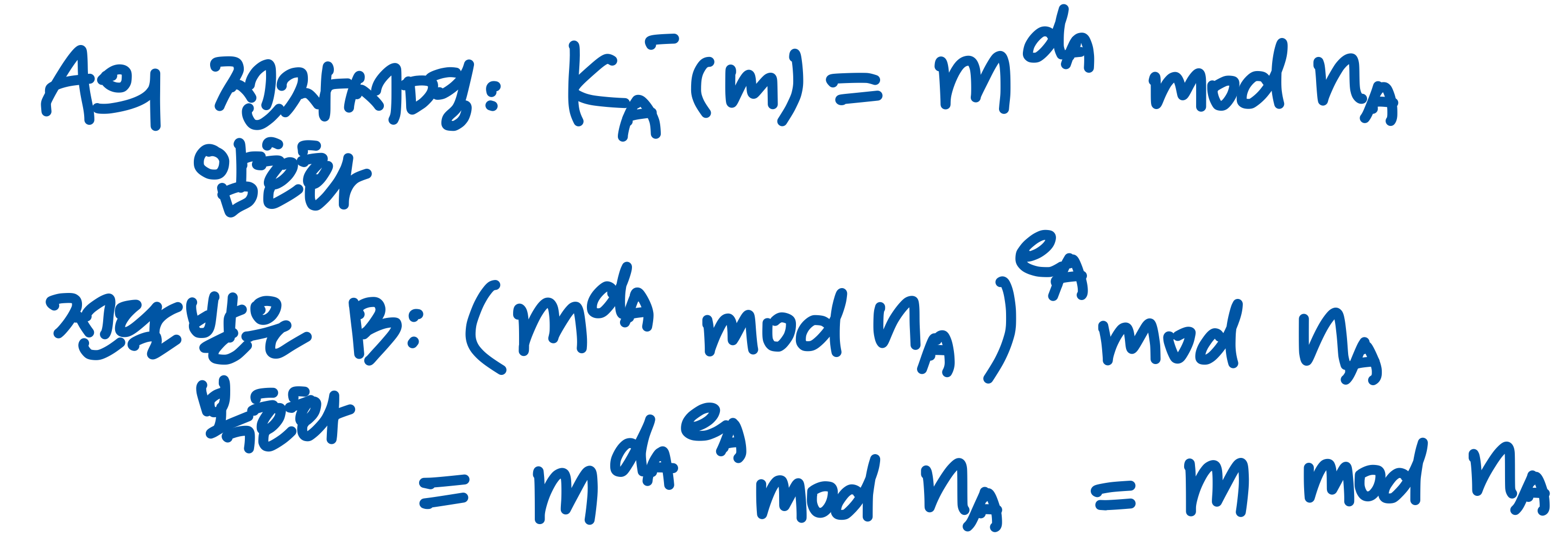
References:
https://com24everyday.tistory.com/299