Deep Learning이란?

• 딥러닝은 머신러닝의 방법론 중 하나
• 선형함수가 아닌 것을 학습 가능
• 인공신경망을 굉장히 깊게 구성하여 학습

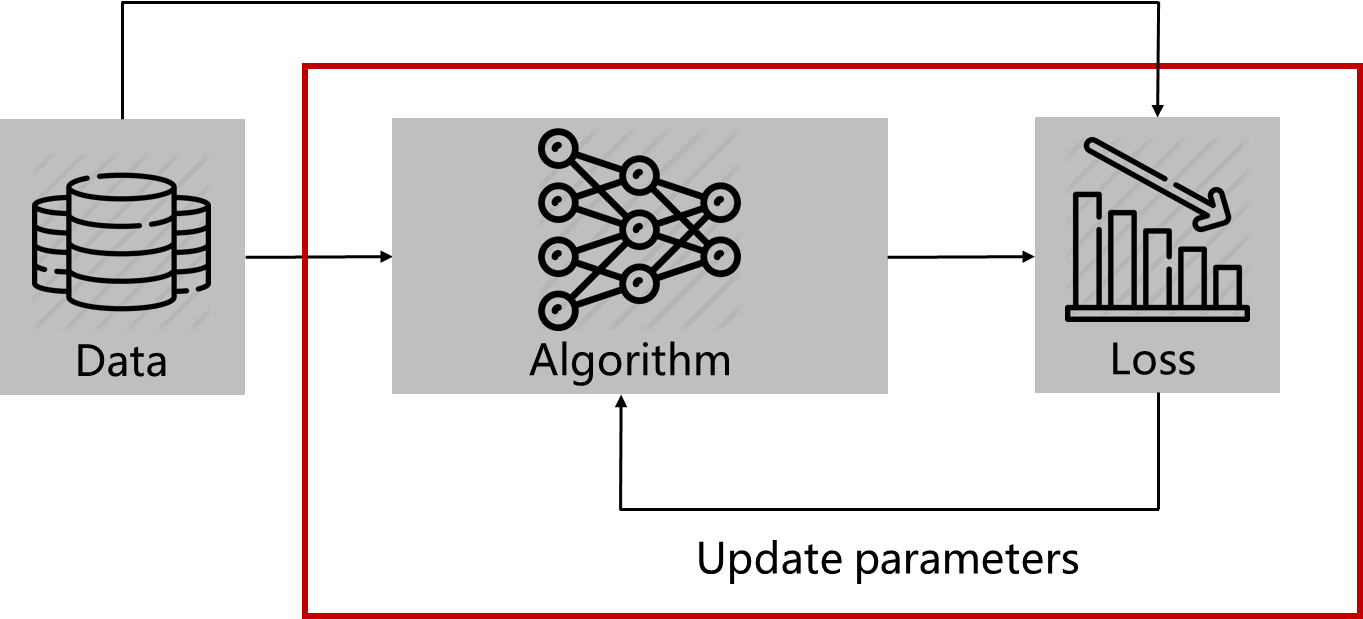
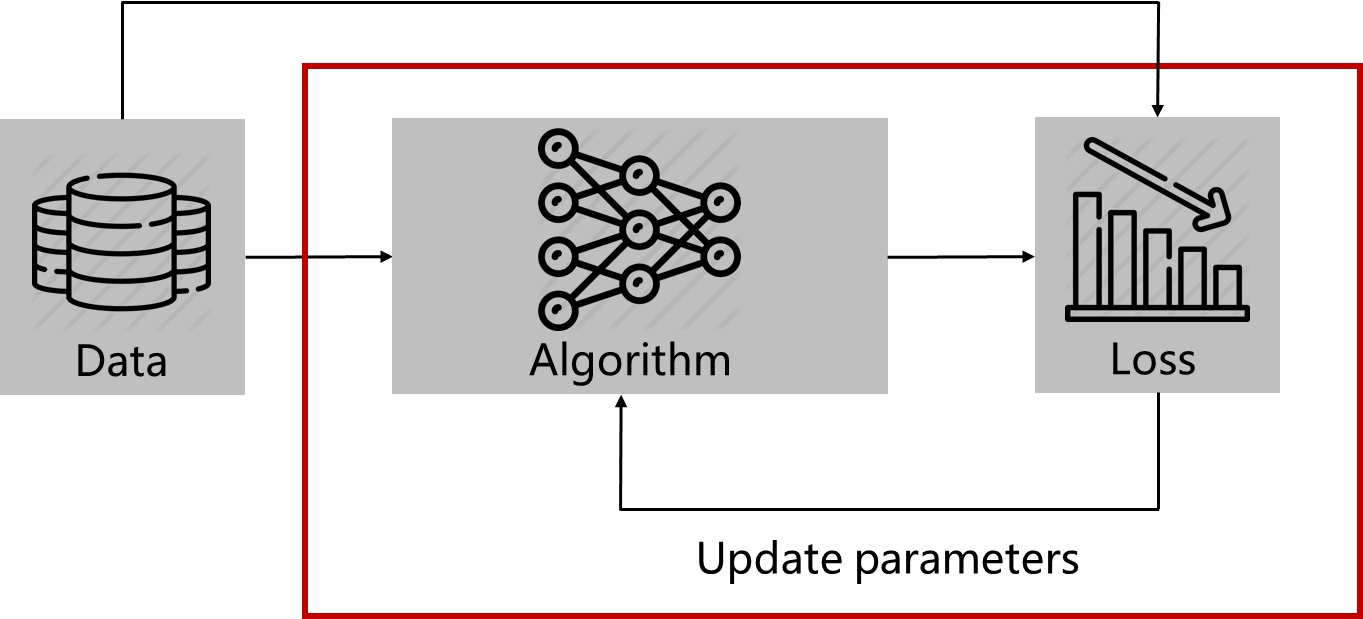
Deep Learning(Machine Learning) Framework

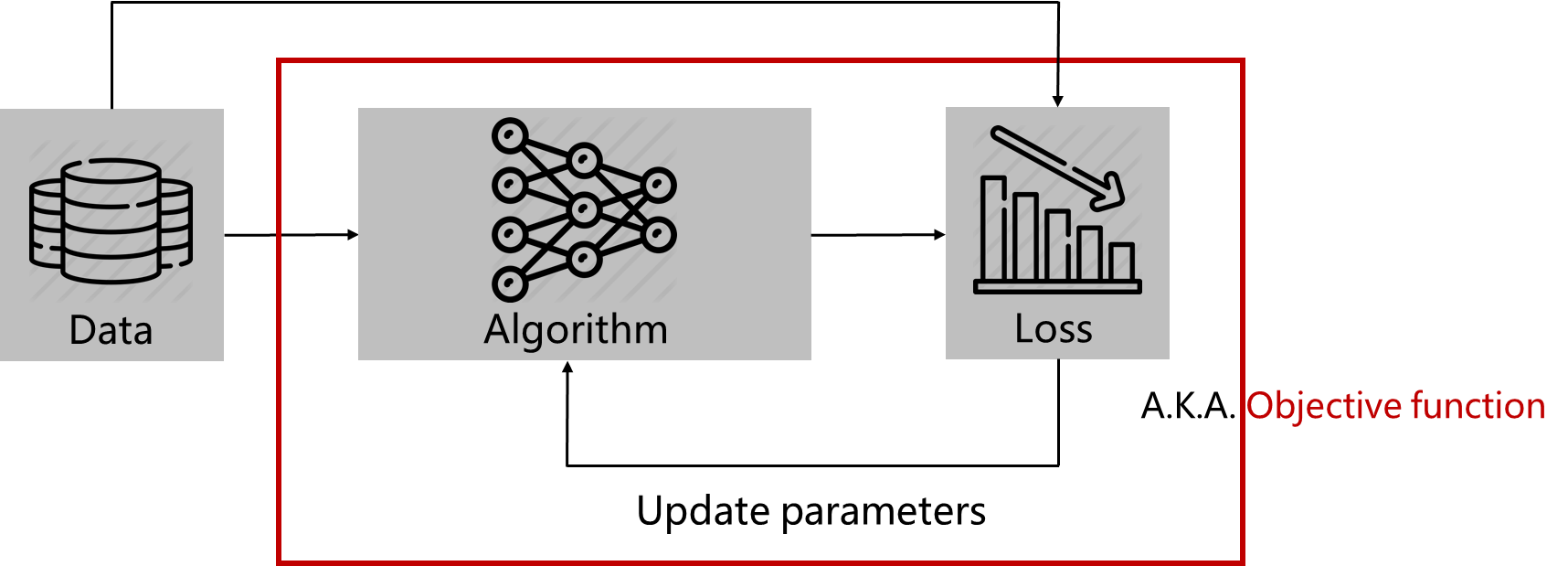
1. Data 준비
2. 알고리즘(파라미터) 통과
3. Loss Function을 통해서 어떤 값을 계산
4. Loss 값을 최대화 또는 최소화 시키는 방향으로 파라미터 업데이트
5. 위 과정을 epoch 만큼 반복

Example : Stock price prediction

• Rule-based system: 전문가가 특정 규칙을 정해서 결과 도출
  
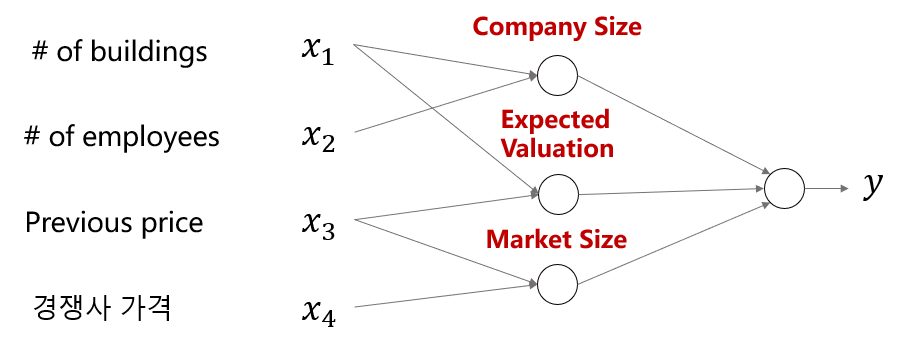
• Neural Networks : 전문적 지식을 요구 X
  
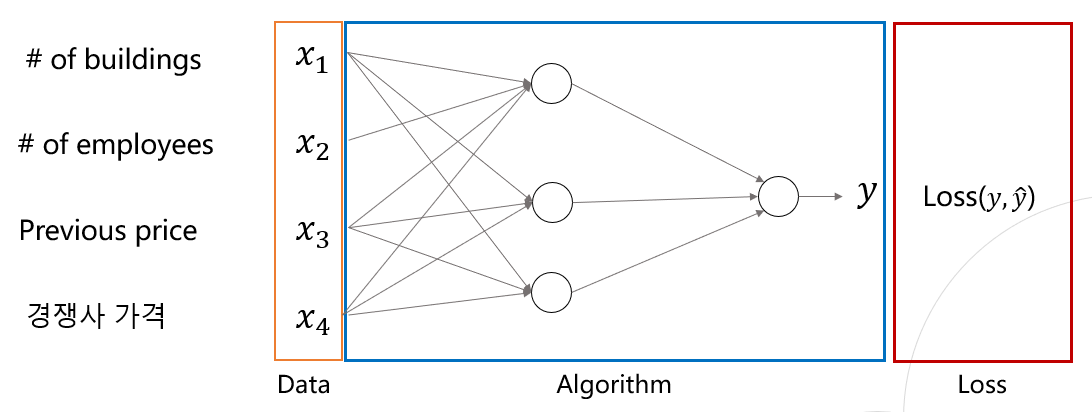
  • 1. Without experts, prior knowledge
  • 2. Machine Learning

Line, Circle and Activation Function

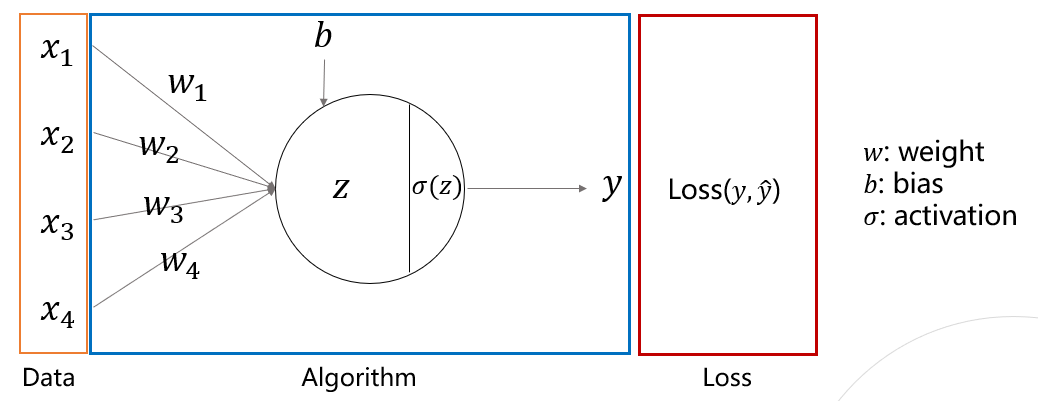
• Line: edge(선), arrow(화살)
  • 각 선은 파라미터를 가지고 다음 노드로 파라미터 값을 곱해주어 전달
• Circle: neuron (뉴런), node(노드)
  • 들어오는 값들을 모두 더하고, 비선형 활성화 함수를 통과시킴

Practice: 의료 데이터 (Regression)

• 모델 디자인 하기
  
• 앞에서 만든 프레임워크와 같이

1. 데이터를 알고리즘에 넣고
2. Loss Function을 통해서 Loss 값을 얻어
3. Loss 값이 최소화 되도록 알고리즘의 파라미터 업데이트
4. 위 과정을 반복

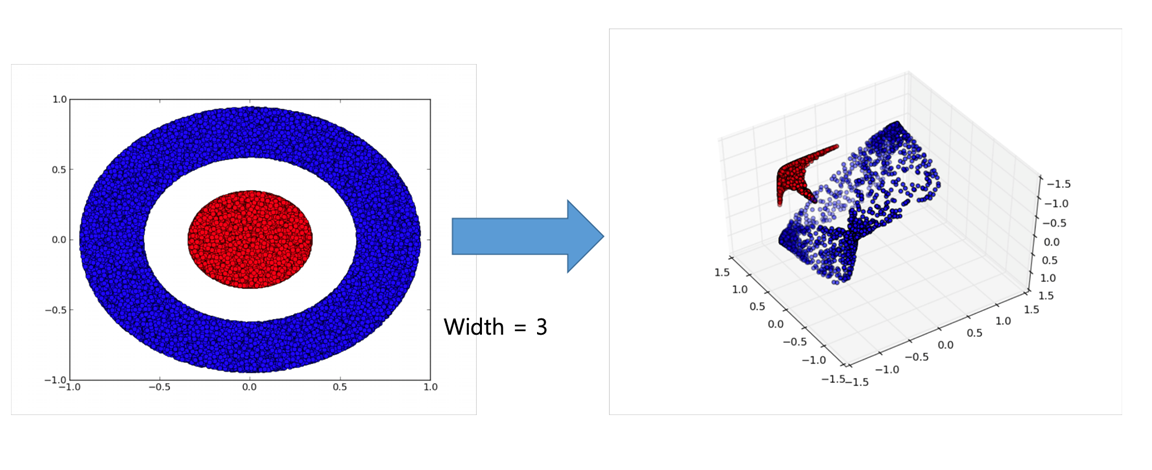
Neural Network가 deep 해지면 이점

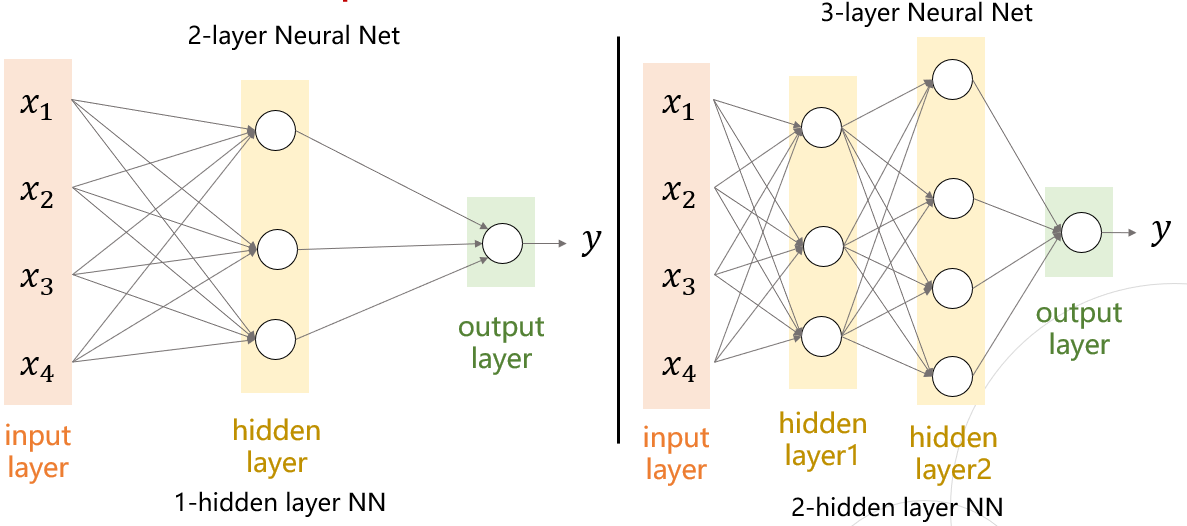
• 비선형인 Acivation Function과의 결합을 통해서 레이어가 깊어져 더 많은 표현 가능
  

Quiz

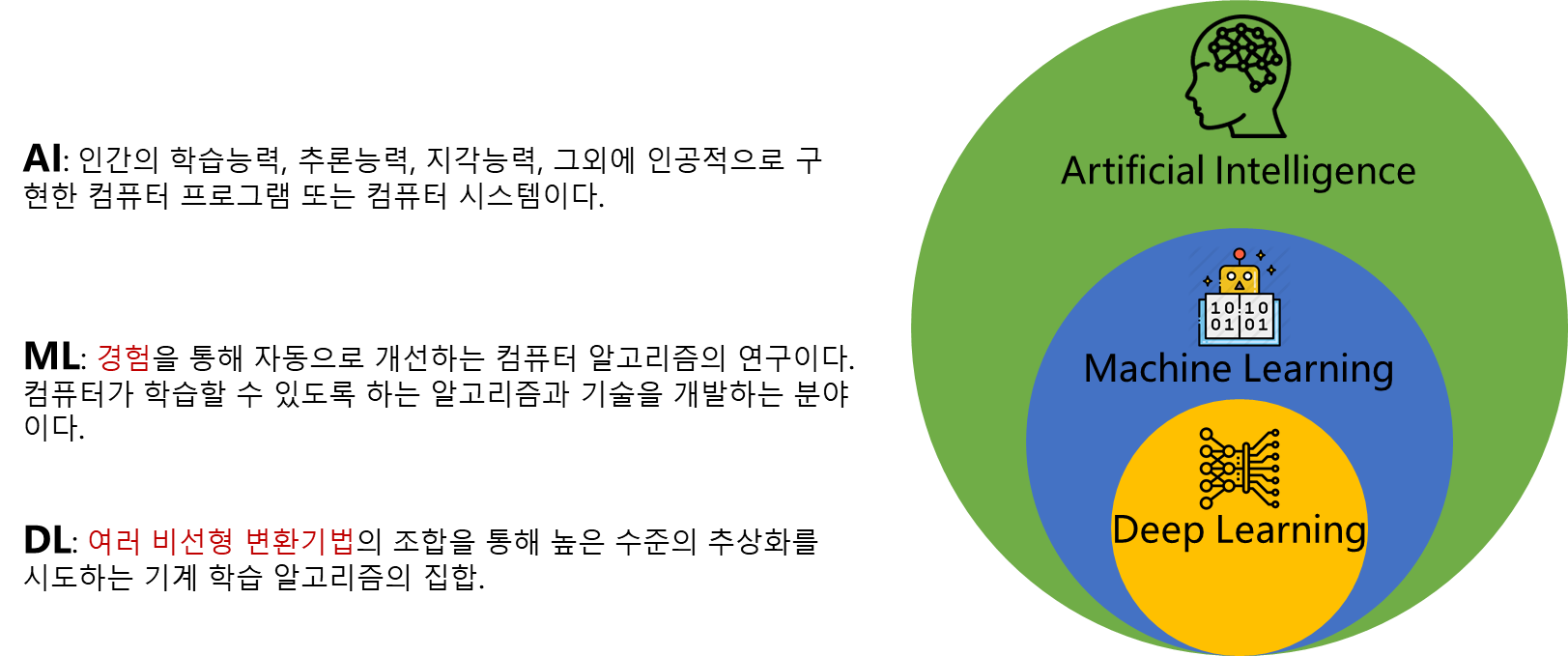
1. AL, ML, DL의 차이?
   

2. ML의 일반적인 framework를 서술해보자!
   

3. NN 모델은 왜 practical하고 useful할까?
   

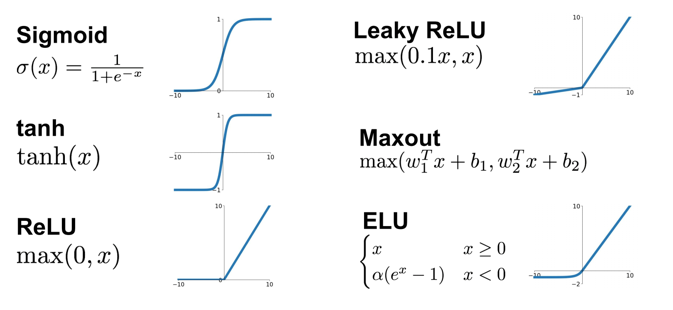
4. 활성화함수가 하는 역할은 무엇인가?
   --> 비선형성을 만들어 준다!!

Activation Function (활성화 함수)

• Activation Function이 없다면 NN은 항상 선형 함수
• 다 층의 많은 개수의 node는 비선형(non-linear)구조를 만들어 문제를 쉽게 해결하도록 만듦
  

Optimization

• How to optimize it?
• How to organize the loss function?

Gradient Descent

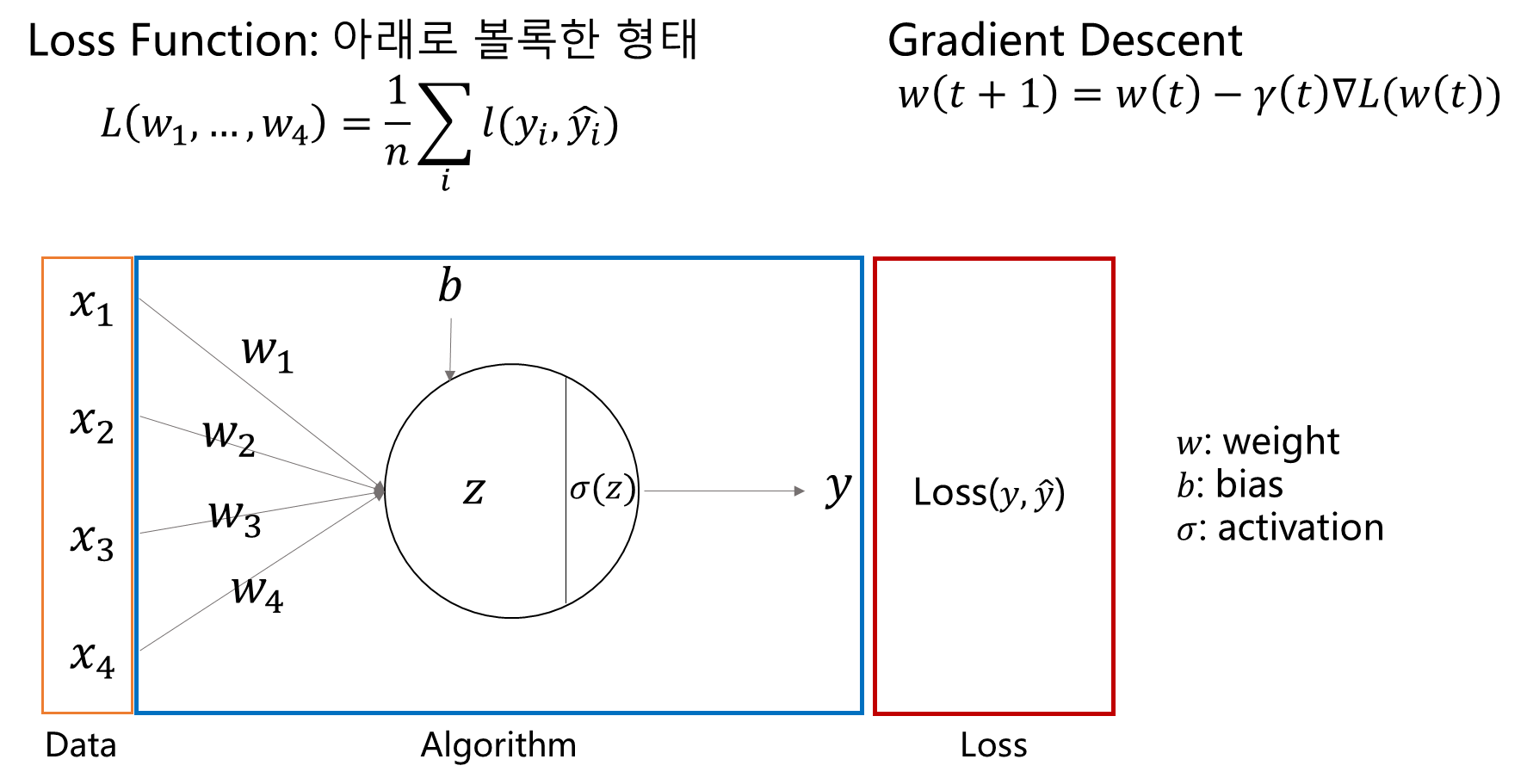
• 모든 y와 $\hat y$에 대해서 손실함수를 계산해야함.
• 또한 손실함수의 모양은 아래로 볼록한 형태여야함.
• $w(t+1) = w(t) - lr\cdot\frac{\partial L}{\partial w(t)}$ --> 파라미터 업데이트 식
  

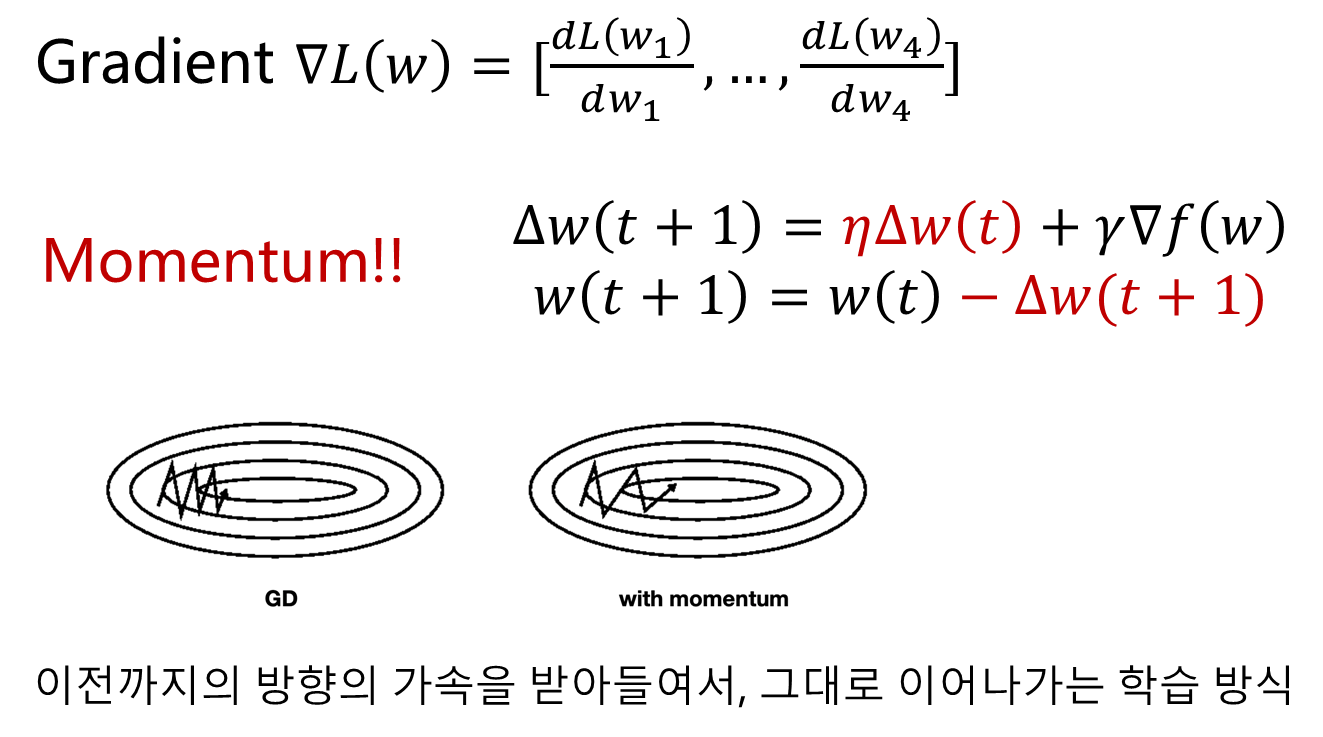
• 기존 방식 lr에 관성을 주어 optimize 속도와 정확도를 높임.

• RMSProp와 Adam역시 Gradient Descent, Momentum에 이어서 발전된 optimizer중 하나

Batch SGD

• Batch: 데이터 묶음
• Batch Gradient Descent
  • $w \leftarrow w- \eta \cdot \nabla L(w)$
• Mini-batch Gradient Descent
  • $w \leftarrow w- \eta \cdot \nabla (\sum_iL(y_i,y_i(w)))$
• Stochastic Gradient Descent --> 확률적 요소가 있으므로 stochastic
  • $w \leftarrow w- \eta \cdot \nabla L(y_i,y_i(w))$

Learning rate decay

• Eta(learning rate)로 적당한 값은?
  • 1. Step decay
       처음 $\uparrow$, 갈수록 $\downarrow$
  • 2. Exponential decay
       $\eta = e^{-t}$
  • 3. Cosine decay
       $sin\theta[0,\frac{\pi}2]$

Pytorch

Pytorch의 비중이 점점 늘어나는 이유?

• 1. 간편성
  • Numpy와 유사함.
  • 매우 pythonic함.
  • Debugging이 쉬운편임.
  • Tensorflow는 버전 업데이트가 잦음.
  • 버전 충돌 이슈가 자주 생김. 불편함.
• 2. 대중성
  • 다양한 최신 기술의 구현이 잘 되어 있음.
  • 반면, Tensorflow는 아님.
  • Google-Deepmind Engineer/Researcher들도 불만을 가짐.

  Numpy

• 다차원 배열 처리에 대해서 빠르고 효율적임
  

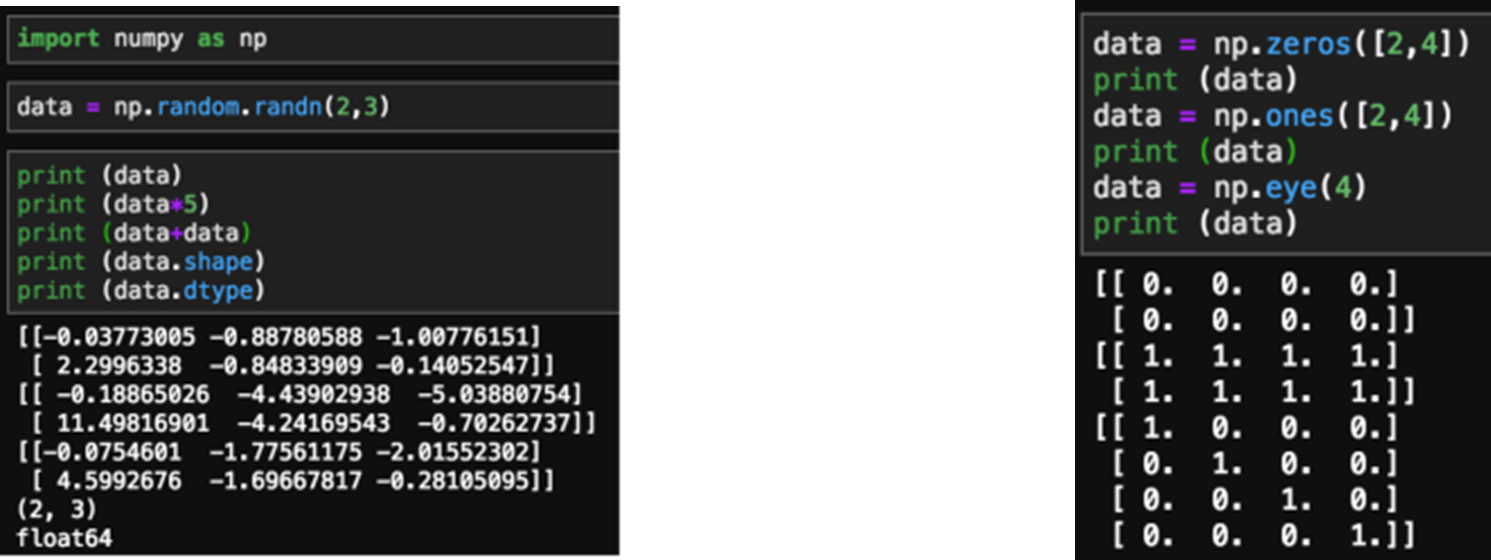
• Matrix 연산, 벡터 내적

  

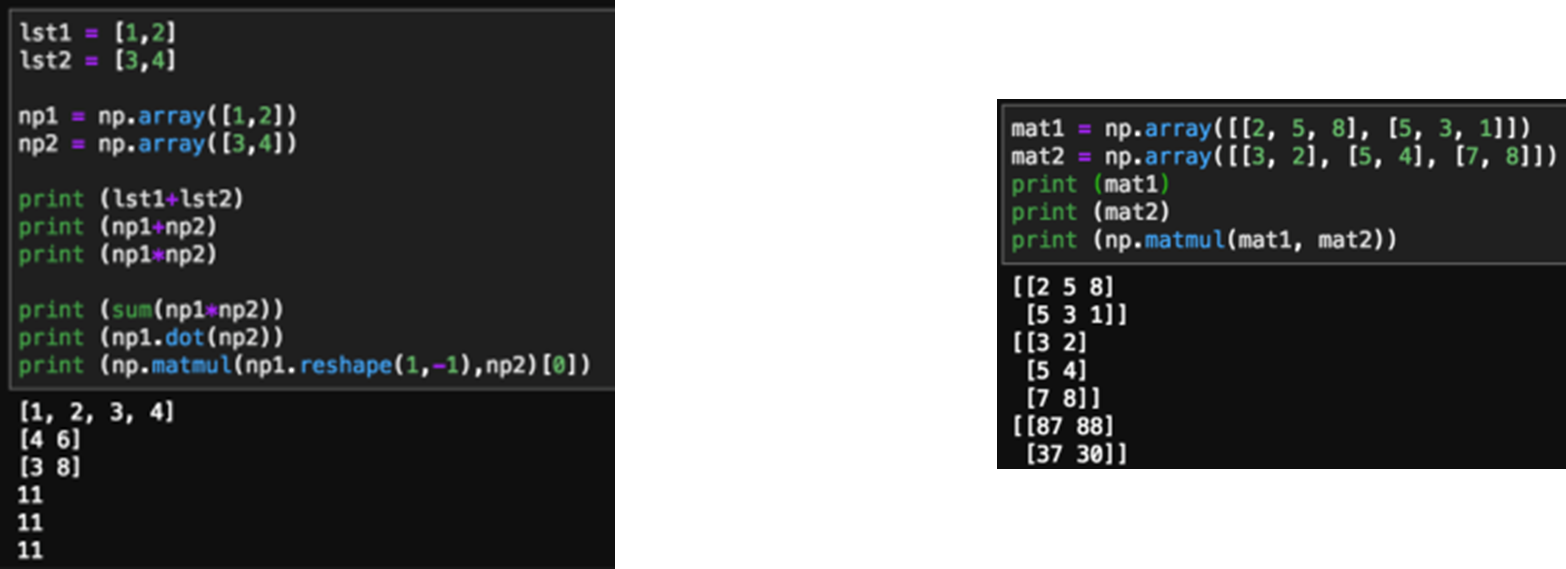
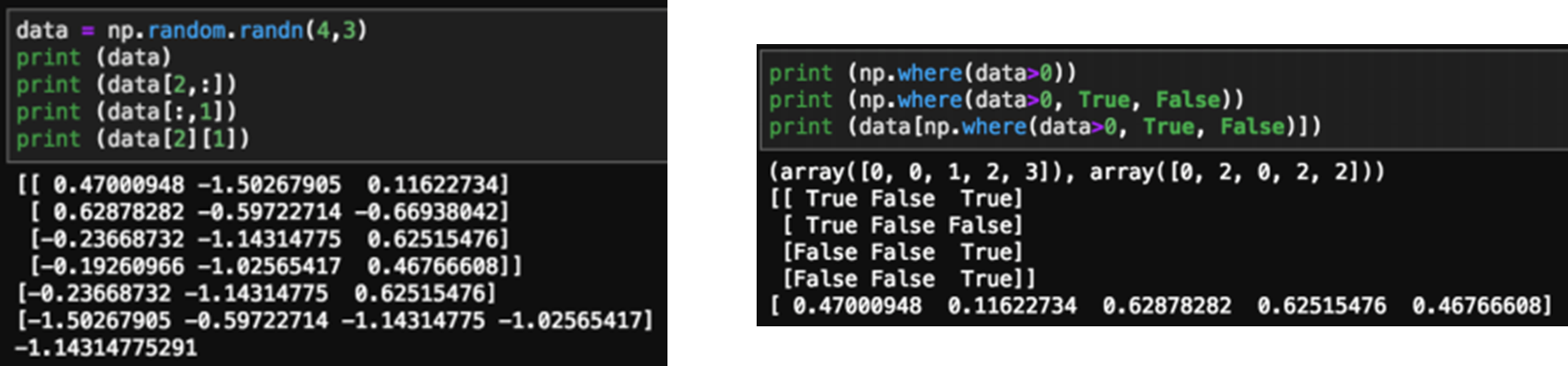
• Indexing/Slicing, Condition
  

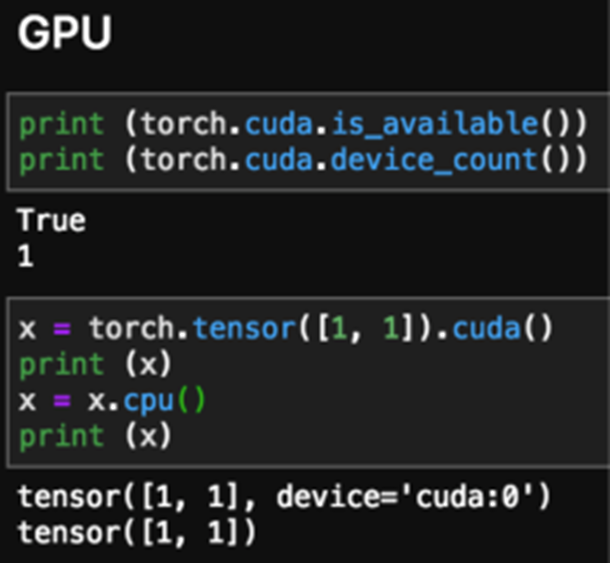
GPU

시나리오

import

import torch 								# pytorch(tensor 생성)
import torch.nn as nn 						# pytorch(네트워크 생성)
import matplotlib.pyplot as plt 			# 시각화
from sklearn import datasets 				# 데이터셋 준비

print(torch.cuda.is_available()) 			# GPU 확인

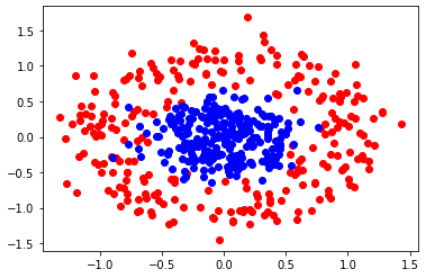
데이터 준비

n_pts = 500 									# 생성 샘플 개수
X, y = datasets.make_circles(n_samples=n_pts, random_state=123, noise=0.2, factor=0.3) # 데이터 생성

x_data = torch.Tensor(X) 						# x 데이터 텐서에 넣기
y_data = torch.Tensor(y.reshape(500, 1)) 		# y 데이터 텐서에 넣기

def scatter_plot():								# 데이터 시각화로 확인
	plt.scatter(X[y==0, 0], X[y==0, 1], color='red')
    plt.scatter(X[y==1, 0], X[y==1, 1], color='blue')

scatter_plot()

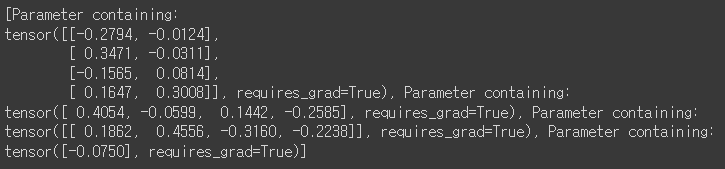
네트워크 모델

class Model(nn.Module):										# class 형태로 네트워크 생성

    def __init__(self, input_size, H1, output_size):		# input,hidden, output layer node 수
        super().__init__()									
        self.linear1 = nn.Linear(input_size, H1)			# layer1 정의
        self.linear2 = nn.Linear(H1, output_size)			# layer2 정의

    def forward(self, x):									# 모델 forward 구조
        x = torch.sigmoid(self.linear1(x))
        x = torch.sigmoid(self.linear2(x))
        return x

    def predict(self, x):
        return 1 if self.forward(x) >= 0.5 else 0

model = Model(2, 4, 1)
print(list(model.parameters()))

Loss

criterion = nn.BCELoss() 										# binary cross entropy Loss
optimizer = torch.optim.Adam(model.parameters(), lr=0.01) 		# Adam Optimizer

Optimizer

epochs = 1000
losses = []

for i in range(epochs):
    optimizer.zero_grad() 										# 1. 파라미터 gradient 초기화
    y_pred = model(x_data) # y_pred = model.forward(x_data)		
    loss = criterion(y_pred, y_data)

    print("epochs: {}, loss: {}".format(i, loss.item()))

    losses.append(loss.item())
    loss.backward() 											# 2. gradient 계산
    optimizer.step() 											# 3. 파라미터 업데이트