Neural Networks (1) _ Loss Function

1. 크로스 엔트로피

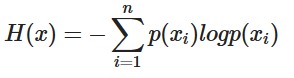
• 크로스 엔트로피는 분류 문제에서 모델의 예측 성능을 측정하는 데 사용되는 중요한 손실 함수입니다. 이 함수는 "모든 샘플에 대해 실제 클래스에 대한 우리의 예측 확률의 -log를 합한 것"으로 해석할 수 있습니다.

1) 예측확률

• 모델은 각 클래스에 대해 어떤 확률을 예측합니다. 예를 들어, 이미지가 고양이인지 개인지를 구분하는 모델이 있다고 가정해 봅시다. 모델은 각 이미지에 대해 '고양이일 확률'과 '개일 확률'을 예측합니다.

2) 실제 클래스와의 비교

• 각 샘플(예: 이미지)에 대해, 우리는 모델이 예측한 '실제 클래스에 해당하는 확률'을 확인합니다. 실제로 고양이인 이미지에 대해, 모델이 '고양이일 확률'을 얼마나 높게 예측했는지가 중요합니다.

3) 크로스 엔트로피 공식의 해석

크로스 엔트로피 손실 함수의 공식은 다음과 같이 해석될 수 있습니다:

• -log(probability): 모델이 실제 클래스에 대해 예측한 확률을 취합니다. 그리고 이 확률의 로그를 취한 다음, 음수를 취합니다 (-log(probability)). 왜 로그를 사용할까요? 로그 함수는 확률이 낮을수록 손실을 크게 만들고, 확률이 높을수록 손실을 작게 만들어 모델이 올바른 클래스에 더 높은 확률을 할당하도록 독려합니다.

• 합산(Summation): 이 연산은 모든 샘플에 대해 수행됩니다. 즉, 각 샘플에 대한 -log(예측 확률) 값을 모두 더합니다. 이렇게 함으로써, 모델이 데이터셋의 모든 샘플에 대해 얼마나 잘 수행하는지 전체적인 측정을 할 수 있습니다.

4) 예시

• 예를 들어, 고양이와 개를 구분하는 모델이 있고, 하나의 고양이 이미지에 대해 모델이 '고양이일 확률'로 0.9 (90%)를 예측했다고 가정해봅시다. 크로스 엔트로피는 이 경우 -log(0.9)가 됩니다. 반대로, 모델이 0.1 (10%)의 낮은 확률을 예측했다면, 크로스 엔트로피는 -log(0.1)이 되어 훨씬 더 큰 손실 값을 갖게 됩니다. -log 함수는 확률이 1에 가까울수록 y값이 0과 가까워지므로 loss가 작아집니다.

5) 요약

• 크로스 엔트로피는 모델이 실제 클래스를 얼마나 '확신'하며 예측하는지를 측정하는 방법입니다. 모델이 올바른 예측에 높은 확률을 할당할수록 손실은 줄어들고, 잘못된 예측에 높은 확률을 할당할수록 손실은 커집니다. 이를 통해 모델이 더 정확한 예측을 하도록 학습됩니다.

• 크로스엔트로피는 주로 분류 문제에서 사용되는 손실 함수입니다. 이 함수는 모델의 예측이 실제 레이블과 얼마나 잘 일치하는지를 측정합니다. 모델이 올바른 예측을 할수록 손실은 작아지고, 잘못된 예측을 할수록 손실은 커집니다. 이렇게 함으로써, 모델이 정확한 예측을 하도록 유도합니다.

2. 그라디언트 디센트(Gradient Descent)

그라디언트 디센트는 머신러닝에서 가장 널리 사용되는 최적화 알고리즘 중 하나입니다. 이 방법은 손실 함수의 최소값을 찾기 위해 사용됩니다. 기본적으로, 그라디언트 디센트는 손실 함수의 '경사(기울기)'를 따라 하강하여, 함수의 최소값을 찾는 과정입니다.

1) 역할

• SGD는 손실 함수를 최소화하기 위해 모델의 가중치를 업데이트하는 최적화 알고리즘입니다.

2) 작동 방식

• SGD는 데이터셋의 각 샘플 또는 소규모 배치에 대해 손실 함수의 기울기(Gradient)를 계산하고, 이 기울기의 반대 방향으로 가중치를 조금씩 업데이트합니다. 이 과정은 손실 함수의 최소값을 찾는 데 도움이 됩니다.

3. 크로스엔트로피와 그라디언트 디센트의 결합

크로스엔트로피 손실 함수는 SGD의 한 단계에서 사용되는 손실 값으로, SGD가 가중치를 어떻게 업데이트할지 결정하는 데 도움을 줍니다. 즉, SGD는 크로스엔트로피 손실 값을 기반으로 가중치를 최적화합니다.

1) 손실 최소화

• 크로스엔트로피를 사용하여 각 단계에서의 모델 손실을 계산합니다. 이 손실은 모델이 얼마나 잘못 예측하고 있는지를 나타냅니다.

2) 손실 함수의 경사 계산

• 모델의 각 매개변수에 대한 손실 함수의 그라디언트(기울기)를 계산합니다. 이 그라디언트는 손실을 줄이기 위해 매개변수를 어떻게 조정해야 하는지를 알려줍니다.

3) 매개변수 업데이트

• 계산된 그라디언트를 사용하여 모델의 매개변수(예: 가중치)를 업데이트합니다. 이는 손실 함수의 최소값을 향해 매개변수를 조금씩 이동시키는 과정입니다.

4. Backpropagation

1) 역할

• Backpropagation은 신경망에서 손실 함수의 기울기(Gradient)를 계산하는 메커니즘입니다. 이는 신경망의 출력 오차를 기반으로 하여, 가중치에 대한 오차의 기울기를 역방향으로 계산합니다. 즉, 네트워크의 출력부터 시작하여 입력 레이어로 거슬러 올라가면서 각 레이어의 가중치에 대한 오차의 기울기를 계산합니다.

2) 목적

• Backpropagation의 목적은 각 가중치가 전체 오차에 얼마나 영향을 미치는지를 파악하는 것입니다. 이 정보는 네트워크가 학습하는 동안 가중치를 어떻게 조정해야 할지 결정하는 데 사용됩니다.

3) Backpropagation과 SGD의 결합

• 신경망 학습 과정에서, backpropagation은 먼저 실행되어 각 가중치에 대한 손실 함수의 기울기를 계산합니다. 이후, 이 기울기는 SGD에 의해 사용되어 실제 가중치의 업데이트를 수행합니다.
• SGD는 backpropagation으로부터 얻은 기울기 정보를 바탕으로, 각 가중치를 업데이트합니다. 이는 보통 가중치 = 가중치 - 학습률 * 기울기의 형태로 수행됩니다.

4) 예시

인풋값 1.37일때, f(x) = 1/x를 미분하면 -(1/x^2)이고 결과는 -0.53

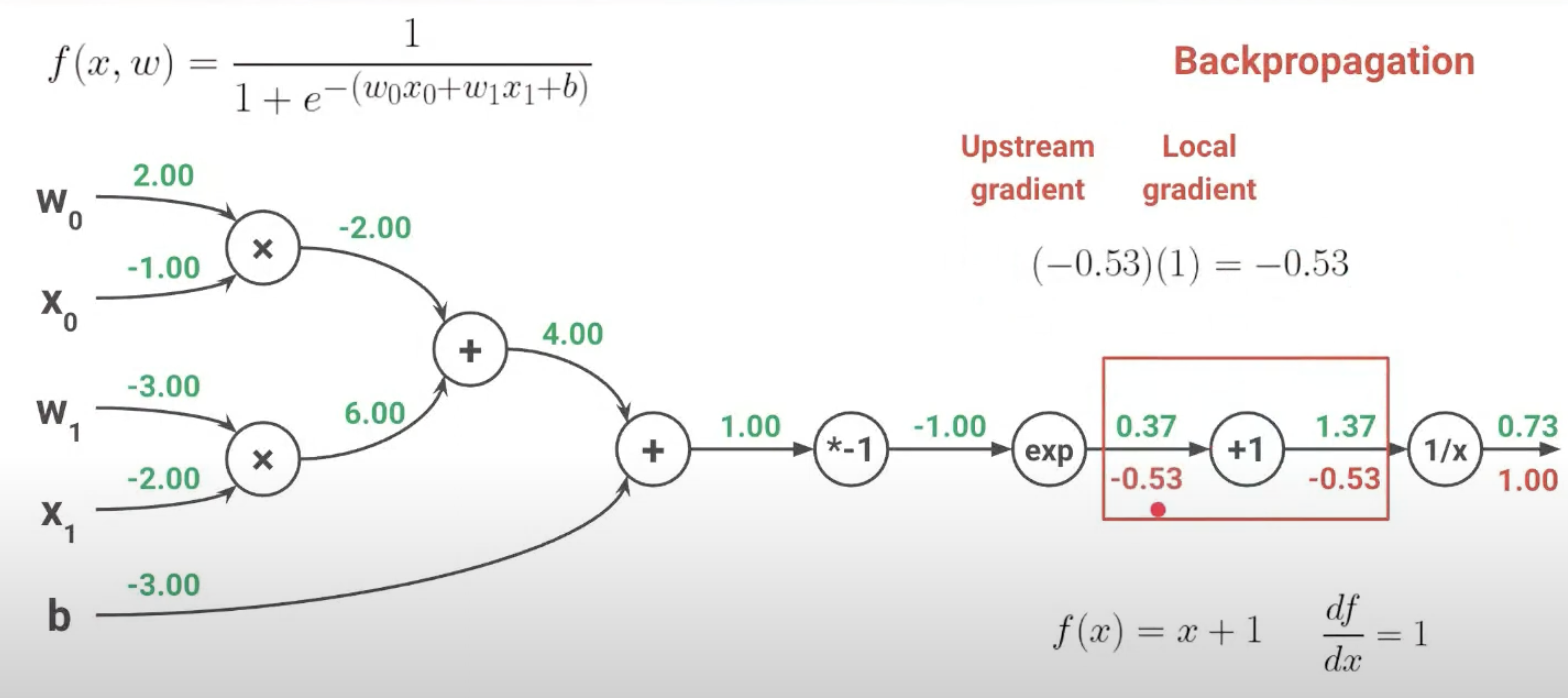
인풋값 0.37일때,f(x) = x + 1이고 이를 미분하면 1이다. 따라서 결과는 1 * -0.53

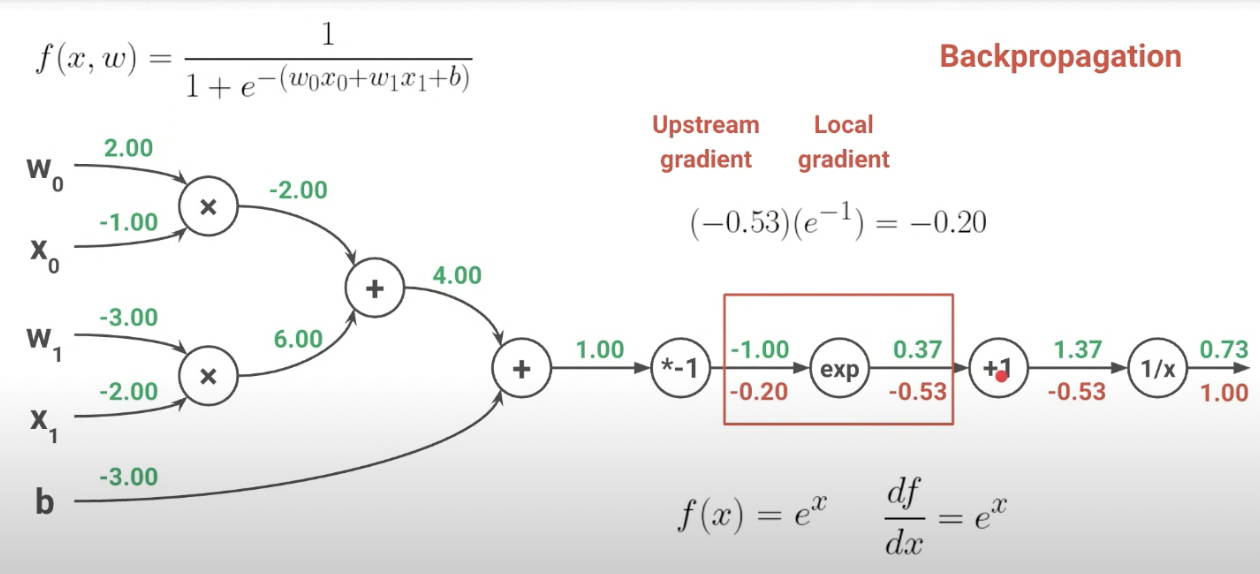
인풋값 -1일때, f(x) = e^-1 이고 이를 미분하면 e^-1이다. 따라서 결과는 -0.53 * e^-1

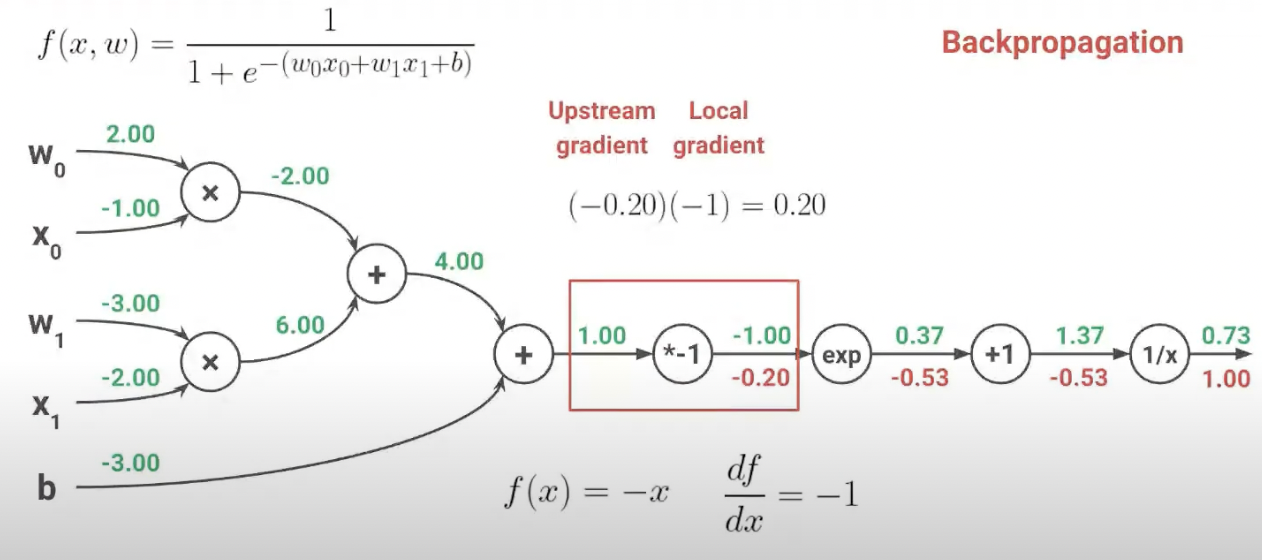
인풋값이 1일때, f(x) = -x이고 이를 미분하면 -1이다. 따라서 결과는 -0.2 * -1

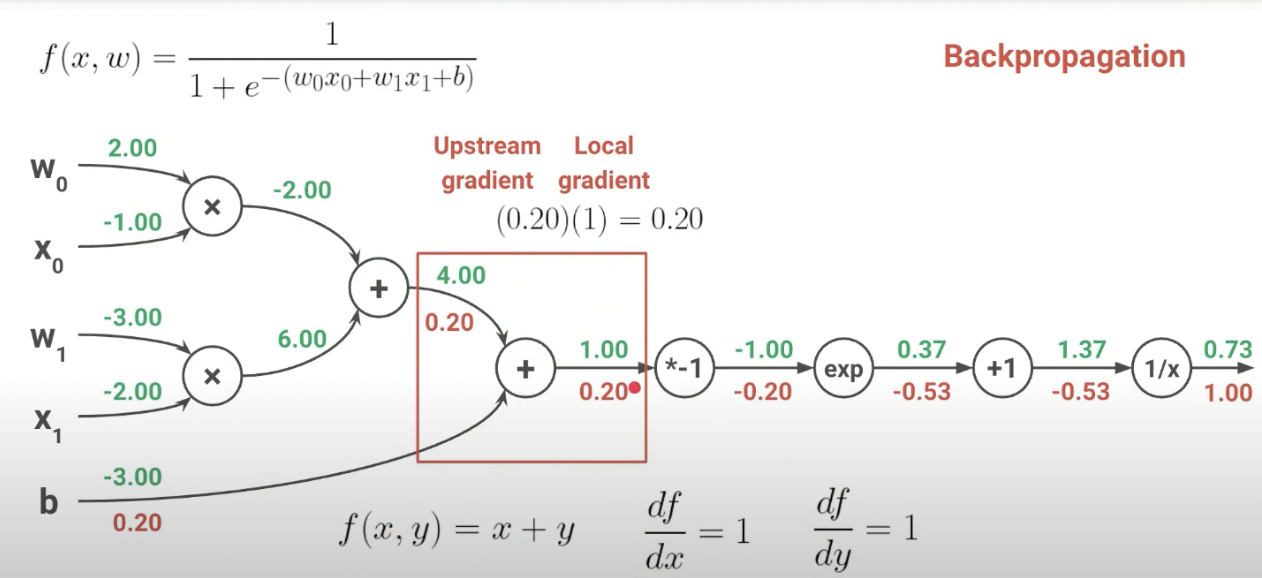
f(x,y) = x + y일때, x쪽 미분하면 1, y쪽으로 미분하면 1이므로 0.2를 전달

f(w,x) = wx일때 x를 미분하면 w, w를 미분하면 x이다. 따라서 w는 0.2 -1, x는 0.2 2