KMP 알고리즘

일반적인 search 알고리즘의 예시

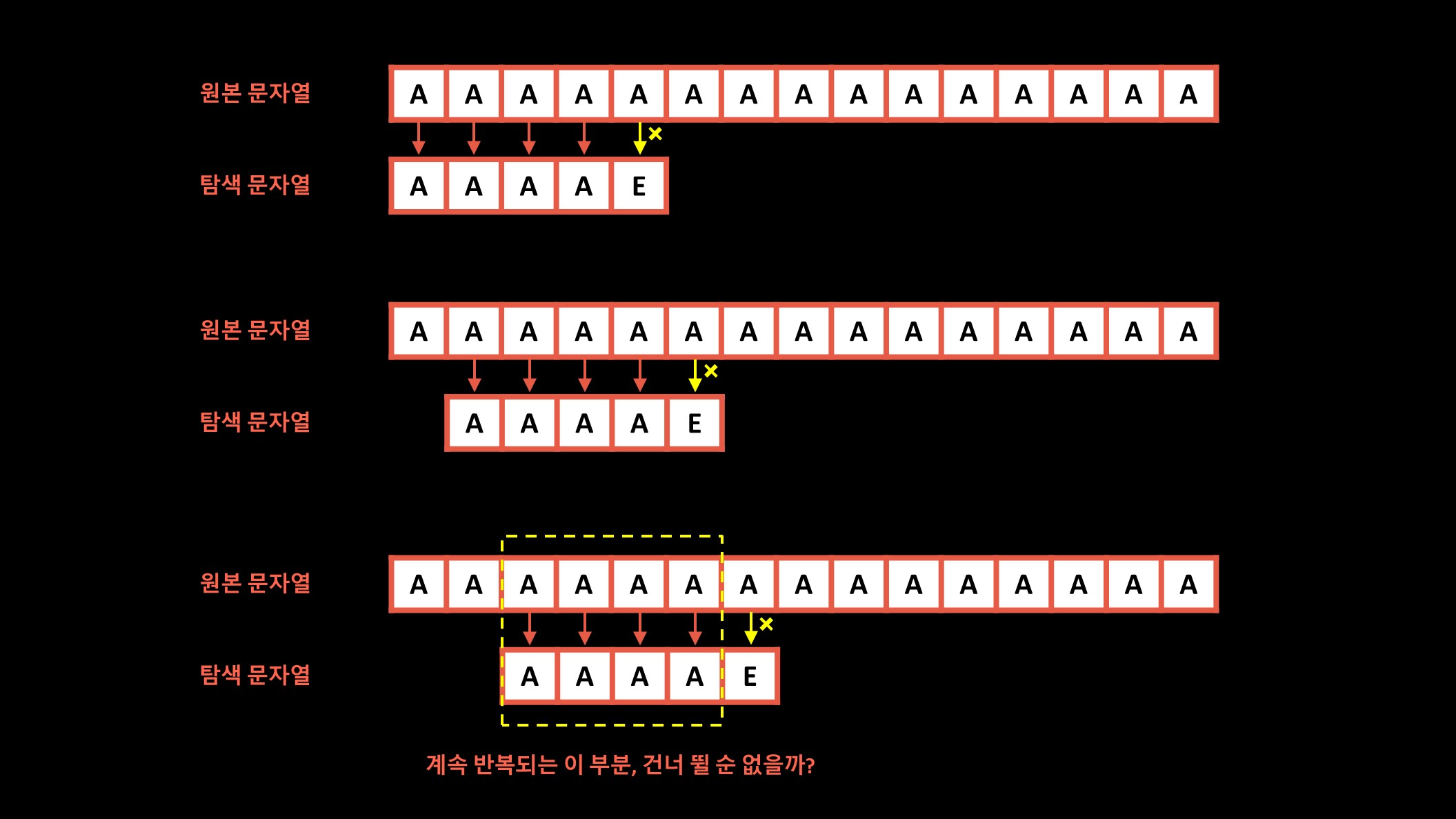
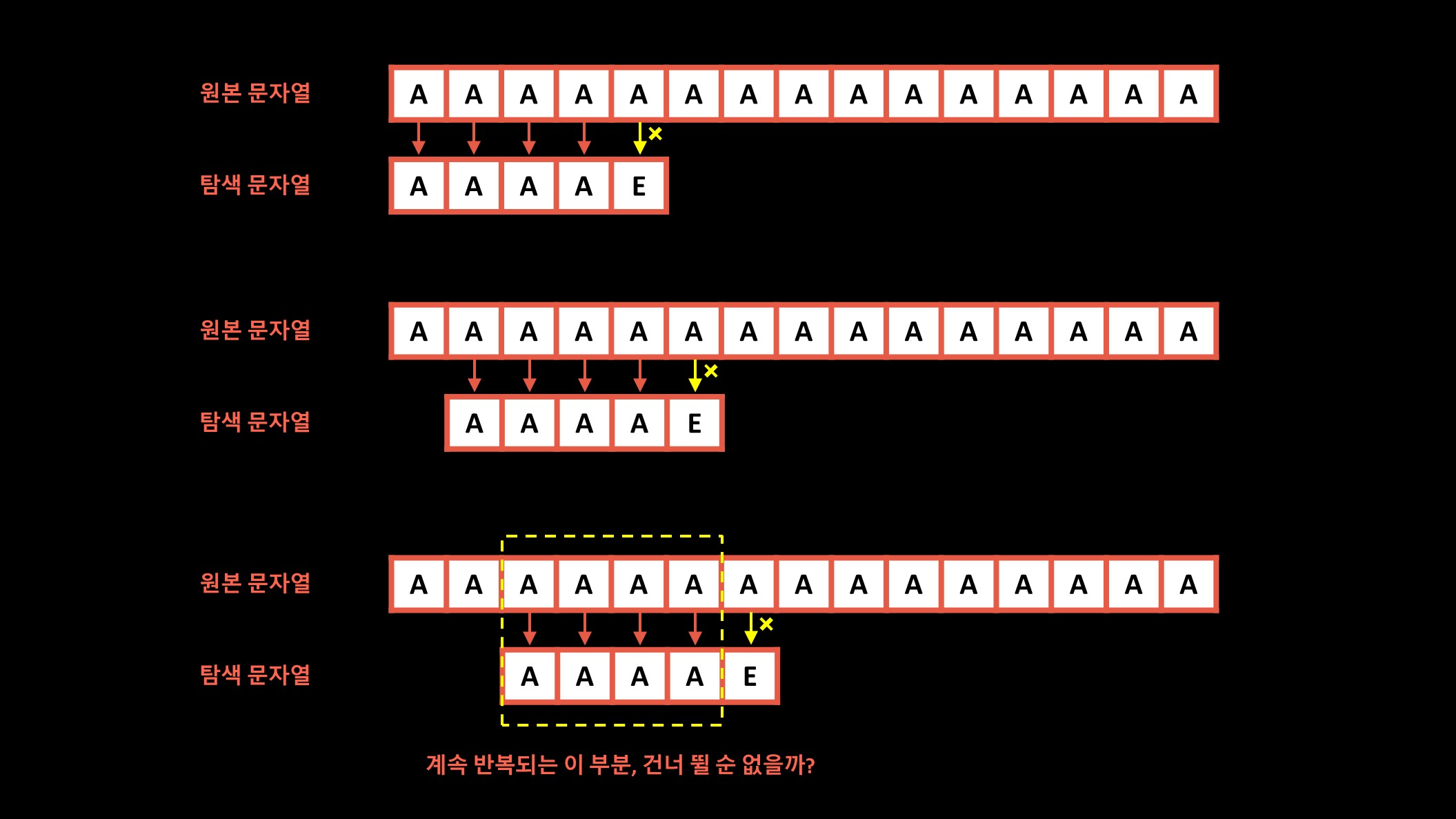
우리가 일반적으로 두 문자열의 공통부분을 탐색할 때 이용하는 방법은 Brute Force 알고리즘이다. 이런 식으로 계속 탐색해나가다보면 원본 문자열의 길이가 N, 탐색 문자열의 길이가 M 일 때 시간복잡도가 O(NM) 이 된다. 하지만 이 방식은 너무 느리기 때문에 KMP 알고리즘을 통해 이 시간 복잡도를 줄여야 한다.

KMP 알고리즘의 시간복잡도

KMP 알고리즘은 시간복잡도 O(n+m)으로 앞서 생각했던 O(NM)보다 월등히 빠르다.

KMP 알고리즘의 원리

접두사와 접미사란 문자열의 가장 앞쪽과 가장 뒤쪽에서 같은 문자열이 나오는 경우를 말한다.
이것을 기본 개념으로 생각하고 KMP 알고리즘을 보면

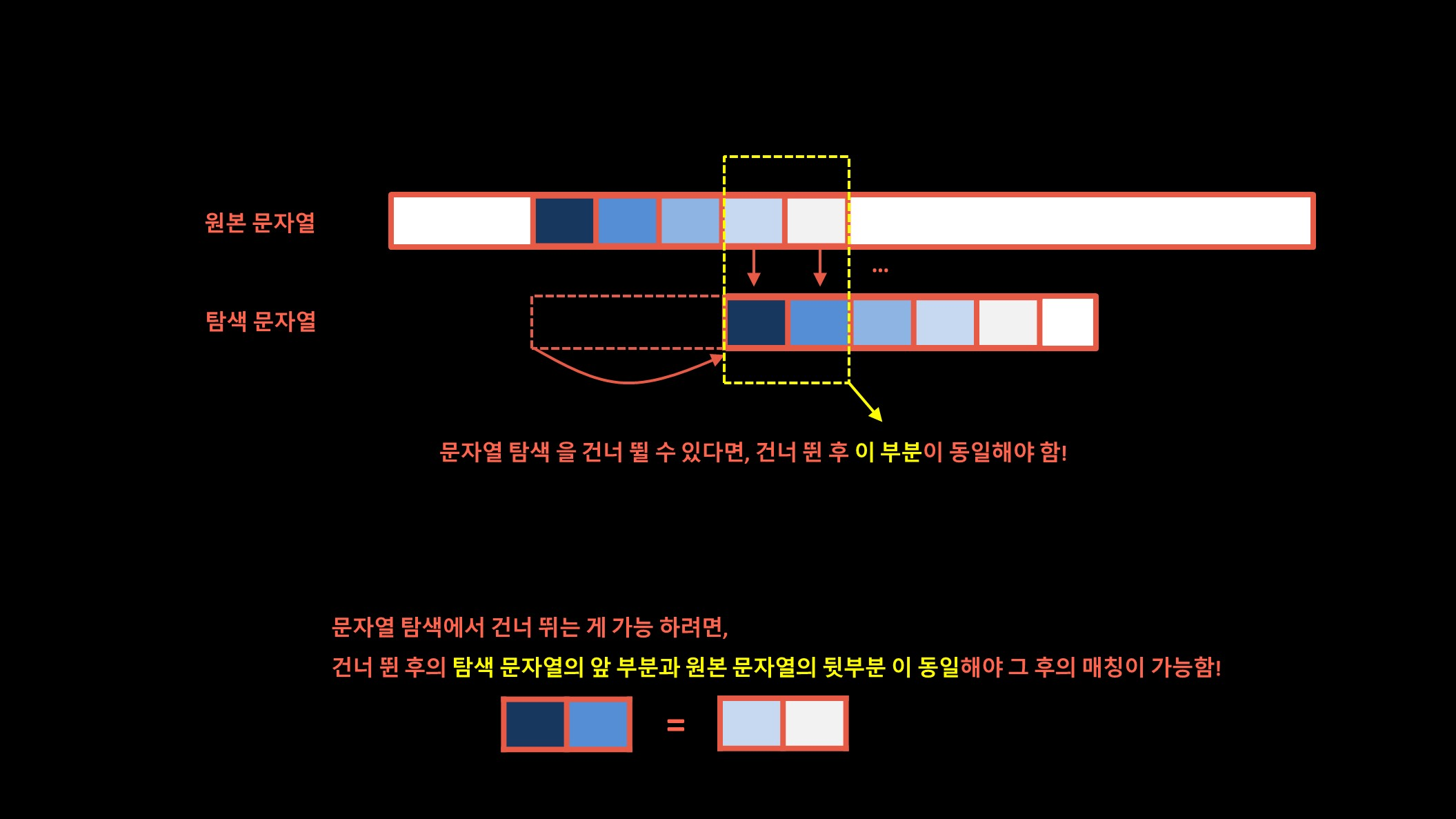
다음과 같은 원리로 알고리즘이 동작을 한다.
문자열 탐색을 건너뛰고 그 뛴 부분이 동일해야 한다.
만약 일정 부분 건너뛰었는데 원본 문자열과 탐색 문자열이 일치하지 않으면 의미가 없으므로 탐색 문자열의 앞 부분과 원본 문자열의 뒷 부분이 동일한 부분까지는 문자열 탐색을 건너 뛸 수 있다.

KMP 알고리즘의 핵심은 탐색 문자열의 앞부분과 원본 문자열의 뒷부분이 동일한 부분까지는 문자열 탐색을 건너 뛸 수 있다는 것이다.

KMP 알고리즘의 구현

백준 7575번 바이러스 문제

우선 전처리 테이블이 필요하다.

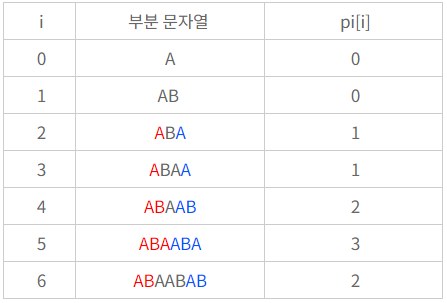
pi는 접두사와 접미사의 최대 길이를 저장해 주는 배열이다.
이것을 코드로 구현하면

전처리 테이블

def makeTable(tmp): # tmp는 패턴
    table = [0] * k # 패턴의 길이와 같은 크기의 테이블을 생성
    i = 0 # i를 이용해서 테이블을 갱신해 나간다.
    for j in range(1,k):
        while i > 0 and tmp[i]!=tmp[j]: # i랑 j랑 다르면 i는 table[i-1]로 돌아간다. 돌아가서 다시 j와 비교한다. 최대 공통 부분들이 Table에 들어 있기 때문에 계속 갱신해 주다가 0이 되면 0을 저장하고 다음 j로 넘어가는 식으로 동작한다.
            i = table[i-1]
        if tmp[i] == tmp[j]: # 만약 같으면 i값에 1을 더하고 table에 넣는다. 
            i += 1
            table[j] = i # i,j 둘다 하나씩 증가시킨다.
    return table

KMP 함수 구현

def kmp(s,f,tmp):
    i = 0 # i를 통해 table 값을 갱신시킨다.
    for j in range(len(s)): 
        while i > 0 and s[j] != f[i]: # i와 j를 비교해서 다르면
            i = tmp[i-1] # 다르게 나온 곳-1번째 table 인덱스로 다시 되돌아가서 다시 비교한다.
        if s[j] == f[i]: # 모든 문자열이 전부 일치하면
            if i == k-1: # i가 패턴의 길이보다 하나 작으면 
                return 1 # 패턴을 찾은 것이므로 1을 반환
            else:
                i += 1 # 모든 문자열이 전부 일치하지 않으면 i를 하나씩 늘려서 비교한다.
    return 0 # 패턴을 못찾은 경우 0을 반환

바이러스인지 판별하는 함수

for i in range(len(m[0])-k+1): # 코드의 길이는 접두사부분까지만 돌리면 되므로 0 부터 패턴의 길이만큼 뺀것+1을 돌리면 된다. 
    t = makeTable(m[0][i:i+k]) # k개의 길이만큼 코드가 같아야 하므로 그것을 패턴으로 makeTable 한다.
    for j in range(1,n): # 프로그램의 개수가 3개 이므로
        c = kmp(m[j],m[0][i:i+k],t) # kmp를 통해 비교해서 k개 이상 겹치는 코드가 존재하는지 판단
        if not c: # 코드가 존재하지 않으면
            c = kmp(m[j][::-1],m[0][i:i+k],t) # 뒤집어서도 비교해본다.
        if not c: # 만약 그래도 존재하지 않으면
            break # 반복문을 탈출하여 No 출력
        if j==n-1: # 만약 바이러스임을 감지하면 Yes 출력
            print('YES')
            exit(0) # 그대로 프로그램 종료
print('NO')

출처 : https://injae-kim.github.io/dev/2020/07/23/all-about-kmp-algorithm.html, https://cantcoding.tistory.com/13?category=873347,https://cantcoding.tistory.com/35