Contribution

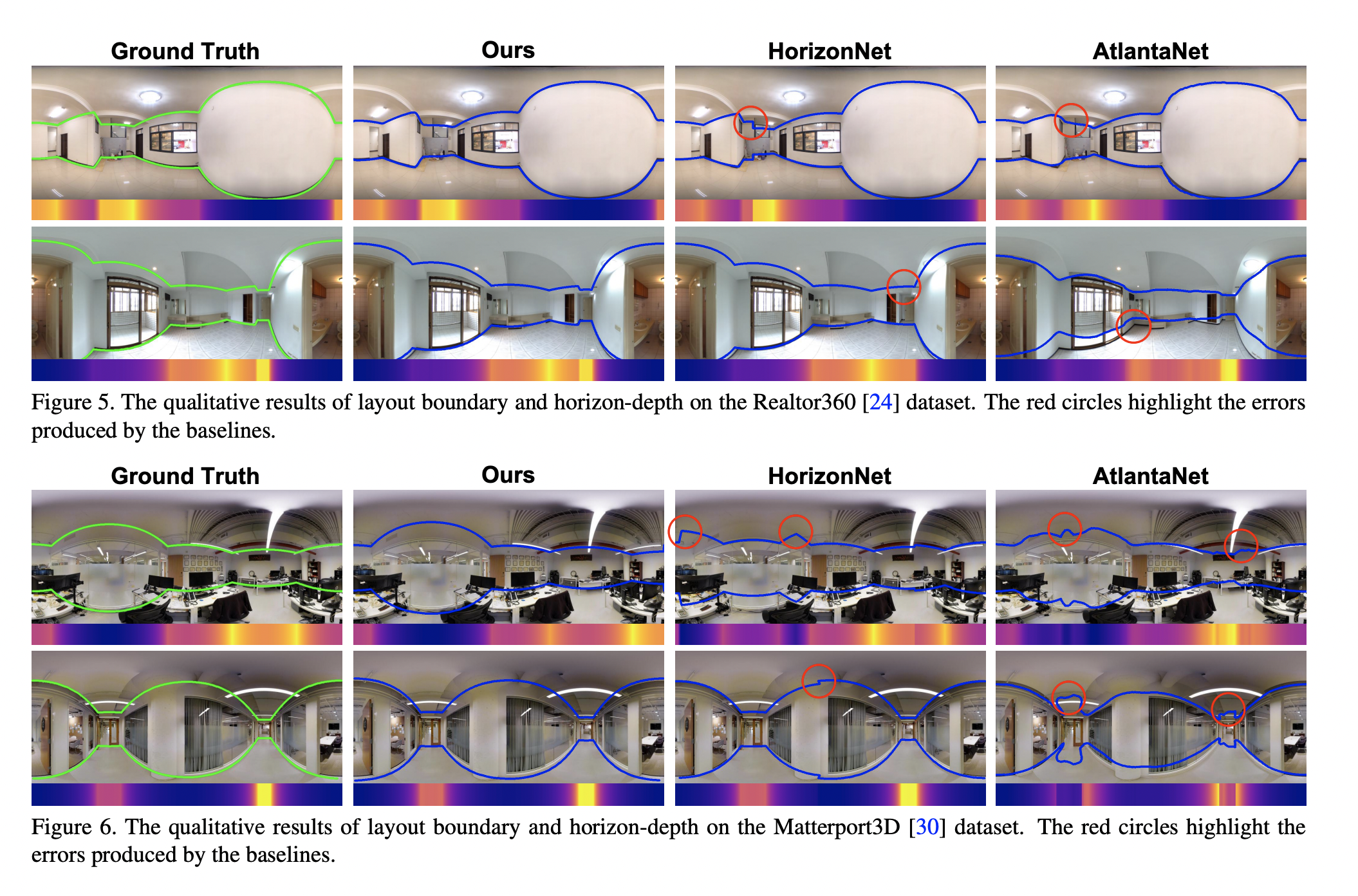
HorizonNet과 같은 기존의 Layout estimation 모델들은 2D Panorama 상에서의 좌표로 loss를 정의하지만 2D 상에서 동일한 오차가 서로 다른 depth value를 가지게 된다.
-> "horizon depth를 활용하자"

Methods

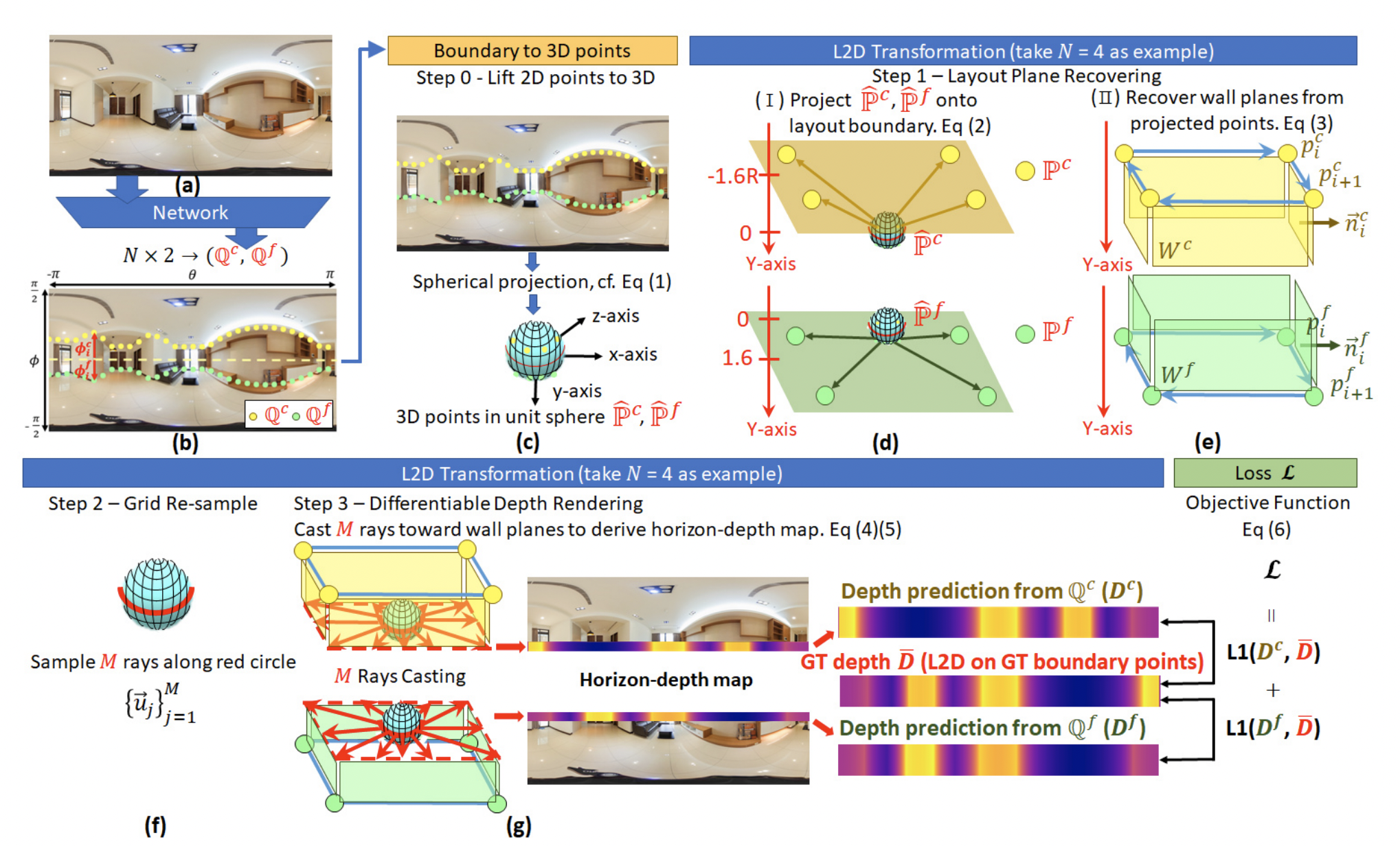
• 벽과 floor/ceiling과의 경계에 해당하는 좌표의 집합 $\mathbb{Q}^f, \mathbb{Q}^c$를 구한다.
• Unit sphere 상에서의 cartesian 좌표계로 변환하여 $\hat{\mathbb{P}}^f,\hat{\mathbb{P}}^c$로 정의한다.

  $\begin{aligned} &S(\theta, \phi)=\left(p_{x}, p_{y}, p_{z}\right) \\ &p_{x}=\cos (\phi) \cdot \sin (\theta) \\ &p_{y}=\sin (\phi) \\ &p_{z}=\cos (\phi) \cdot \cos (\theta) \end{aligned}$

• $\hat{\mathbb{P}}$의 모든 점들을 boundary로 projection 한다. $R$는 카메라의 높이와 카메라 center로부터 천장까지의 거리의 비율을 의미한다.

  $\begin{aligned} p_{i}^{f} &=\hat{p}_{i}^{f} * \frac{1.6}{\hat{p}_{i}^{f}(y)}, &p_{i}^{c} =\hat{p}_{i}^{c} * \frac{-1.6 R}{\hat{p}_{i}^{c}(y)} \end{aligned}$

• $y$축의 unit vector인 $\hat{y}$와 boundary 좌표의 벡터를 외적하여 벽의 normal vector $\vec{n}$을 구한다. $t_i$는 plane 방정식의 offset을 의미하며 $N$개의 벽에 대한 plane 방정식 집합 $\{W_i\}_{i=1}^N$을 구한다.
• $M$개의 ray와 wall plane의 교차점을 통해 horizon-depth map을 얻는다.

  $d_{j, i}^{f}=-\cfrac{t_{i}^{f}}{\vec{u}_{j} \cdot \vec{n}_{i}^{f}}$

• Loss function으로는 L1 loss를 사용한다.
  $\mathcal{L}=||D^f-\bar{D}||_1+||D^c-\bar{D}||$

Results

Reference

• https://github.com/fuenwang/LED2-Net