3.1 Node Embeddings
-
Recap: Traditional ML for graphs
- Given an input graph, extract node, link and graph-level features, learn a model that maps features to labels
- Input graph → Structured features → Learning algorithm → Prediction
-
Graph tepresentation learning
- Graph representation learning alleviates the need to do feature engineering every single time → Automatically learn the features
- Learn how to map node in a d-dimensional space and represent it as a vector of d numbers
- Call it this vector of d numbers as feature representation or embedding
- This vector captures the structure of the underlying network that we are interested in analyzing or making predictions over
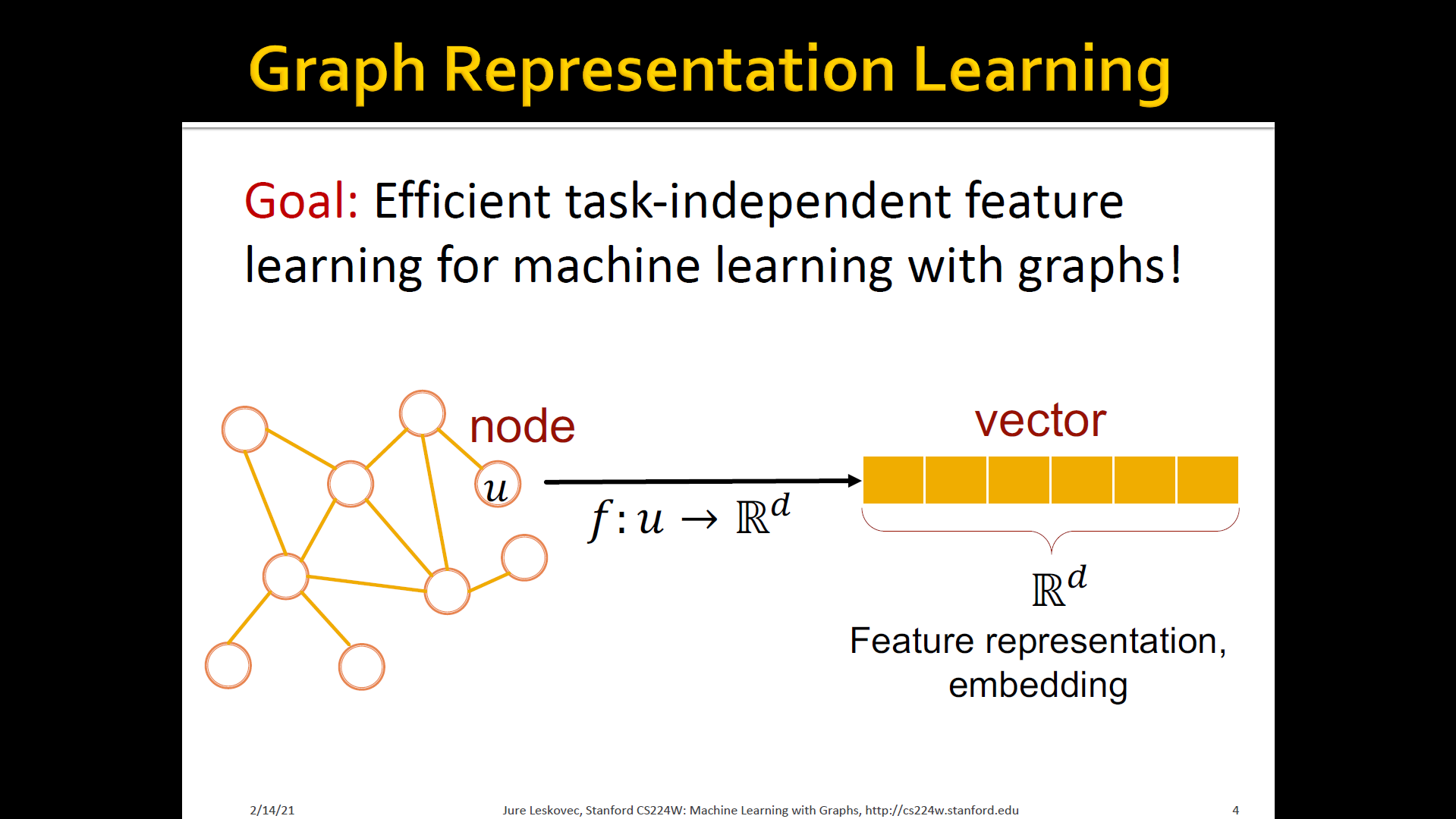
- This vector captures the structure of the underlying network that we are interested in analyzing or making predictions over
-
Why embedding?
- Task: Map node into an embedding space
- Similarity of embeddings b/t nodes indicates their similarity in the network
- For example: Both nodes are close to each other (connected by an edge)
- Encode network structure information
- Potentially used for many downstream predictions
- Node classification, Link prediction, Graph classification, Anomalus node detection, Clustering and so on
Encoder and Decoder
- Assume we have a graph :
- is the vertex set
- is the adjacency matrix (assume binary)
- For simplicity: no node features or extra information is used
-
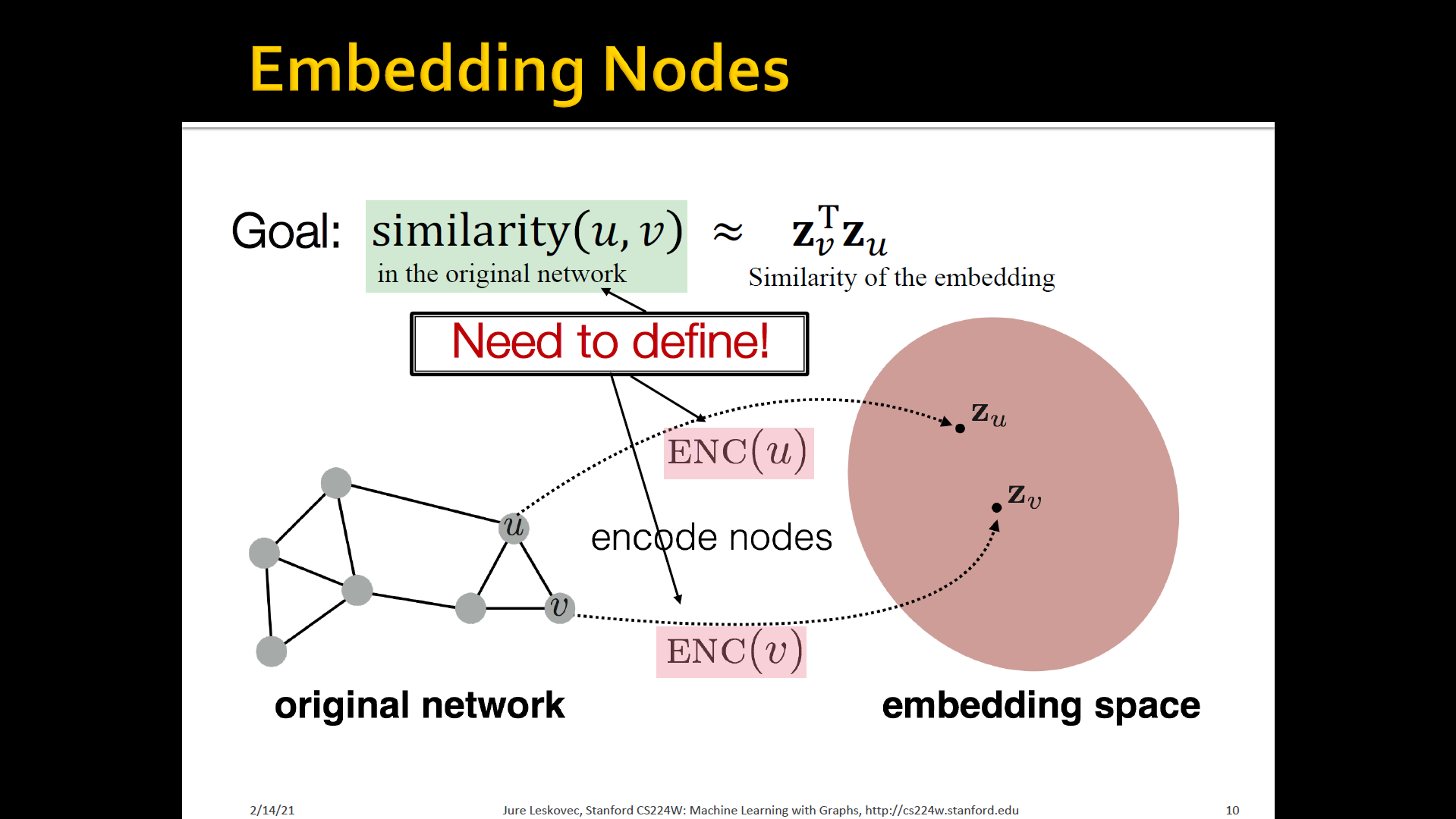
Embedding nodes
- Encode nodes so that similarity in the embedding space (e.g, dot-product) approximates similarity in the graph
- To learn encoder that encodes the original networks as a set of node embeddings
-
Learning node embeddings
- Encoder maps from nodes to embeddings
- Define a node similarity function (i.e, a measure of similarity in the original network)
- Decode maps from embeddings to the similairty score
- Optimize the parameters of the encoder
-
Two key components
- Encoder: maps each node to a low-dimensional vector
- Similarity function: specifies how the relationships in vector space map to the relationships in the original network
-
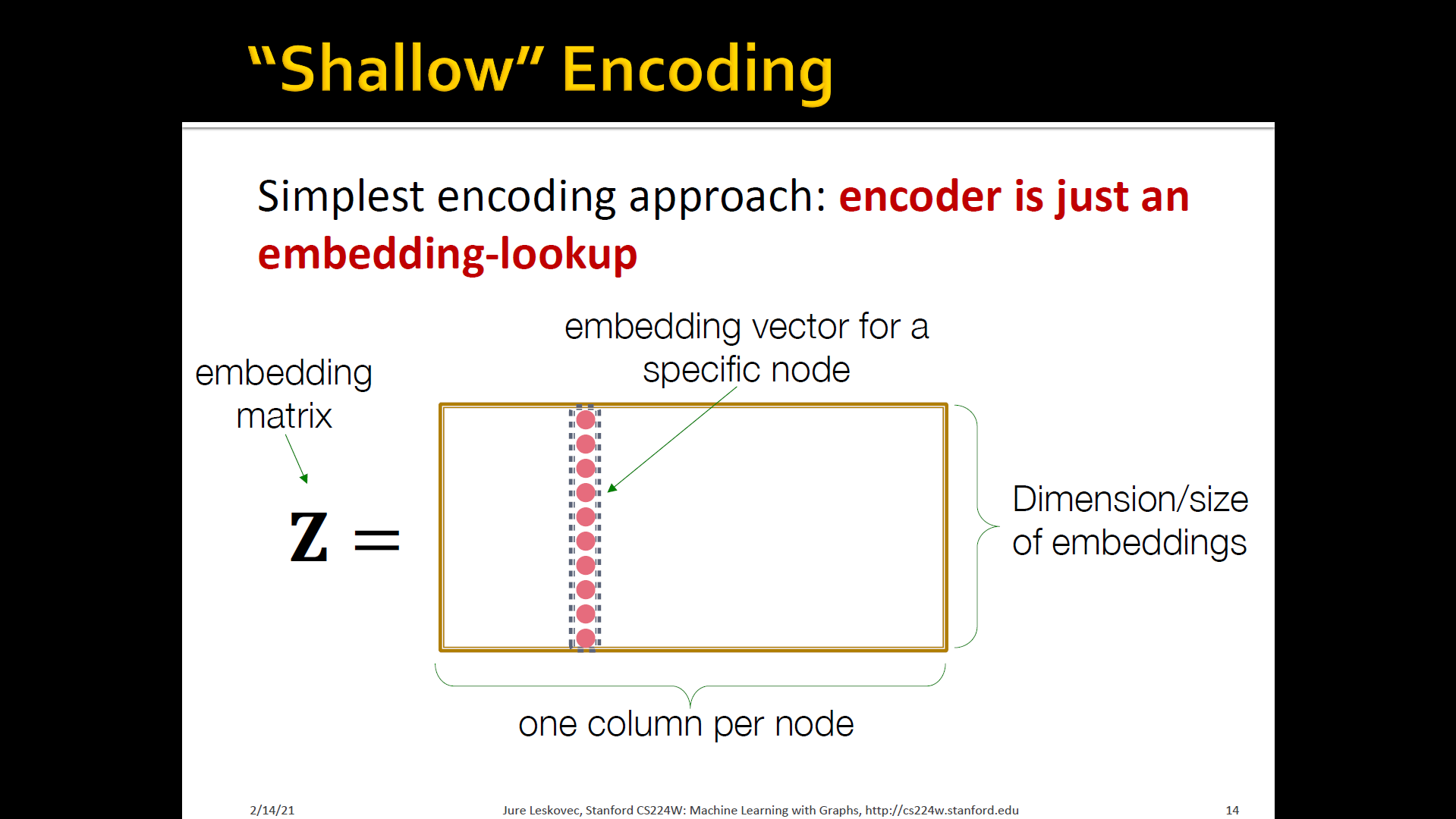
Shallow eEncoding
- Simplest encoding approach: Encoder is just an embedding-lookup
- Each node is assigned a unique embedding vector (i.e, we directly optimize the embedding of each node): DeepWalk, Node2Vec


-
Encoder + Decoder framework
- Shallow encoder: embedding lookup
- Parameters to optimize: which contains node embeddings for al nodes
- Decoder: based on node similarity
- Objective: maximize for node pairs that are similar according to our node similairty function
-
How to define node similarity?
- Should two nodes have a similar embedding if they
- are linked?
- share neighbors?
- have similar "structural roles"?
- Similarity definition that uses random walks, and how to optimize embeddings for such a similarity measure
- Should two nodes have a similar embedding if they
Summary
3.2 Random walk approaches for node embddings
- Notation
- Vector : The embedding of node (what we aim to find)
- Probability : The (predicted) probability of visiting node on random walks starting from node . (Our model prediction based on
- Non-linear functions used to produce predicted probabilities
- Softmax function: Turns vector of real values (model predictions) into probabilities that sum to 1
- Sigmoid function: S-shaped function that turns real values into the range of (0, 1)
- Random walk
- Given a graph and a starting point(node), we select a neighbor of it at random, and move to this neighbor
- Then we select a neighbor of this point at random, and move to it
- The (random) sequence of points visited this way is random walk on the graph
- Random walk embeddings: probability that and co-occur on a random walk over the graph
- Estimate probability of visiting node on a random walk starting from node using some random walk strategy
- Optimize embeddings to encode these random walk statistics
- Similarity in embdding space(Here: dot product = ) encodes random walk "similarity"
- Why random walks?
- Expressitivity: Flexible stochastic definition of node similarity that incorporates both local and higher-order neighborhood information
- IDEA: if random walk starting from node visits with high probability, and are similar (high-order multi-hop information)
- Efficiency: Do not need to consider all node pairs when training; only need to consider pairs that co-occur on random walks
- Expressitivity: Flexible stochastic definition of node similarity that incorporates both local and higher-order neighborhood information
- Un-supervised feature learning
- Intuition: Find embedding of nodes in -dimensional space that preserves similarity
- IDEA: Learn node embedding such that near by nodes are close together in the network
- Given a node , how do we define neraby nodes?
- ... neighborhood of obtained by some random walk strategy
- Feature learning as Optimization
- Given
- Our goal is to learn a mapping
- Log-likelihood objective
- is the neighborhood of node by strategy
- Given node , we want to learn feature representations that are predictive of the nodes in its random walk neighborhood
-
Random walk optimization
- Run short-fixed length random walks starting from each node in the graph using some random walk strategy
- For each node collect , the multiset of nodes visited on random walks starting from
- can have repeat elements since nodes can be visited multiple times on random walks
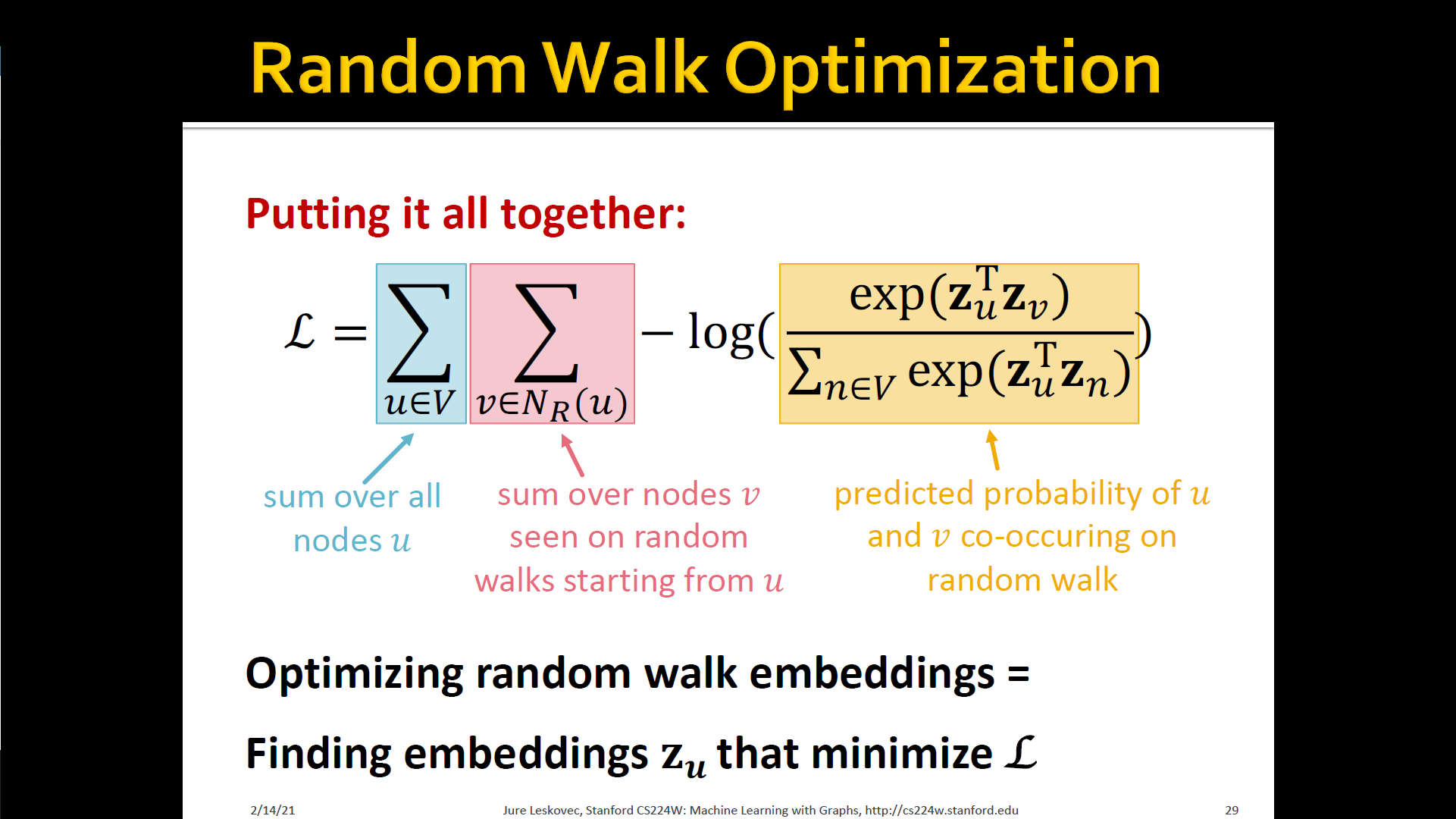
- Optimize embeddings according to: Given node , predicts its neighbors
- → maximum likelihood objective
- Equivalently,
- Intuition: Optimize embeddings to maximize the likelihood of random walk co-occurrences
- Parameterize using softmax:




-
Stochastic Gradient Descent
Random walks summary
Node2Vec
- How sould we randomly walk?
- So far, we have described how to optimize embeddings given a random walk strategy
- What strategies should we use to run these random walks?
- Simplest idea: Just run fixed-length, unbiased random walks strating from each node (DeepWalk)
- The issue is that such notion of similarity is too constrained
- Simplest idea: Just run fixed-length, unbiased random walks strating from each node (DeepWalk)
- Overview of Node2Vec
- Goal: Embed nodes with similar network neighborhoods close in the feature space
- We frame this goal as a maximum likelihood optimization problem, independent to the downstream prediction task
- Key observation: Flexible notion of network neighborhood of node leads to rich node embeddings
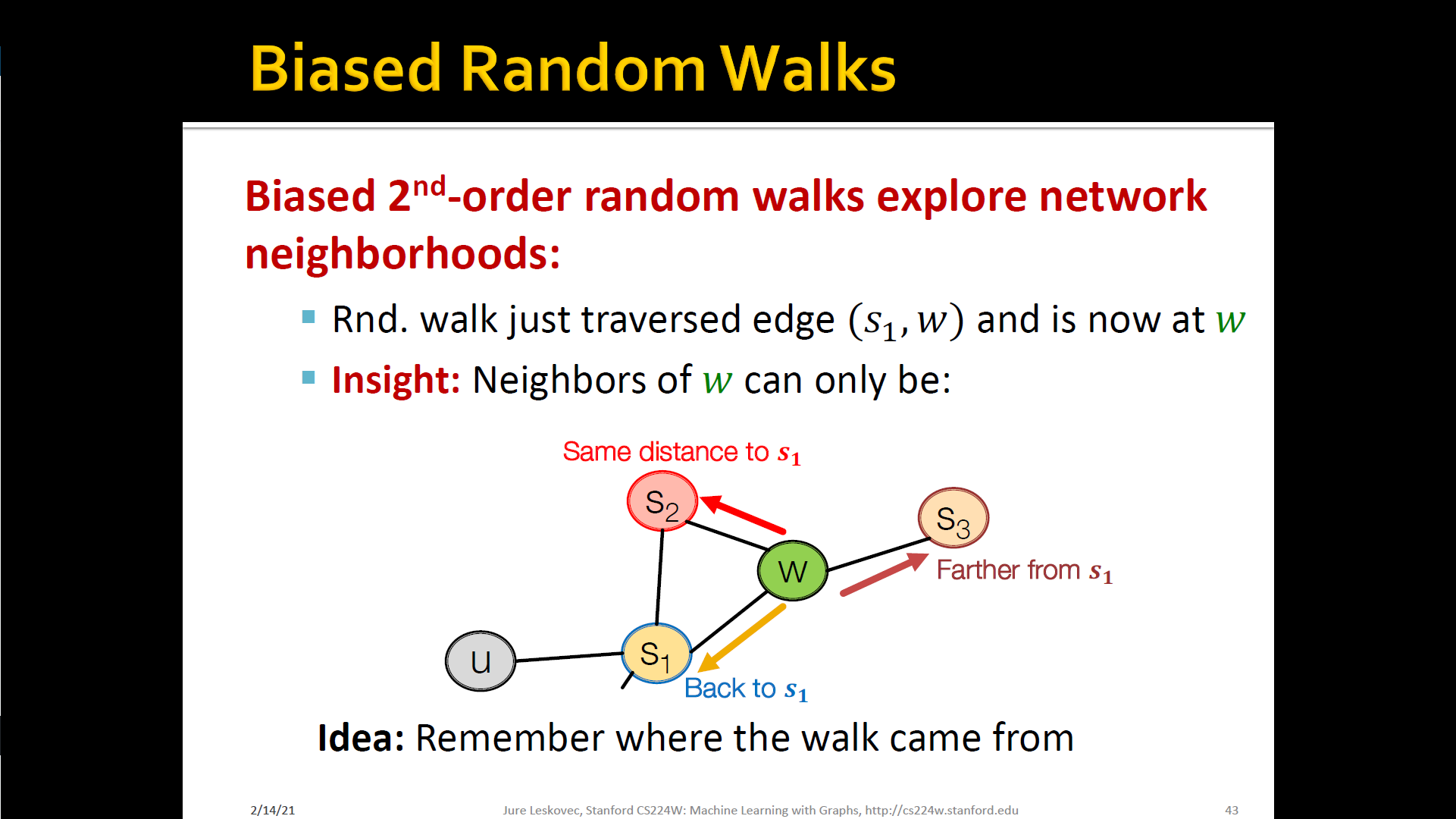
- Develop biased order random walk to generate network neighborhood of node
- Node2Vec : Biased walks
- IDEA: use flexible, biased random walks that can trade-off b/t local and global vies of the network
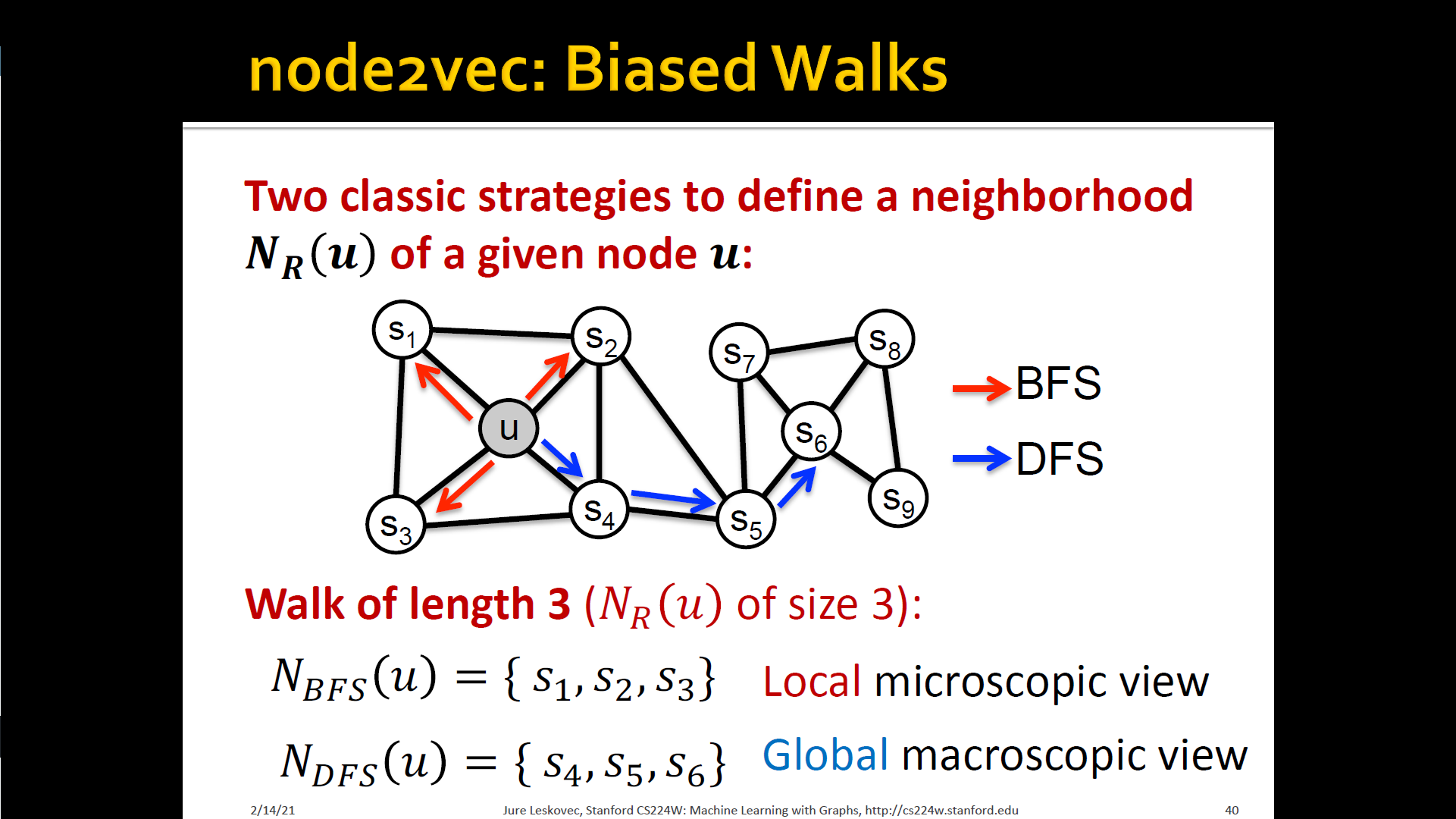
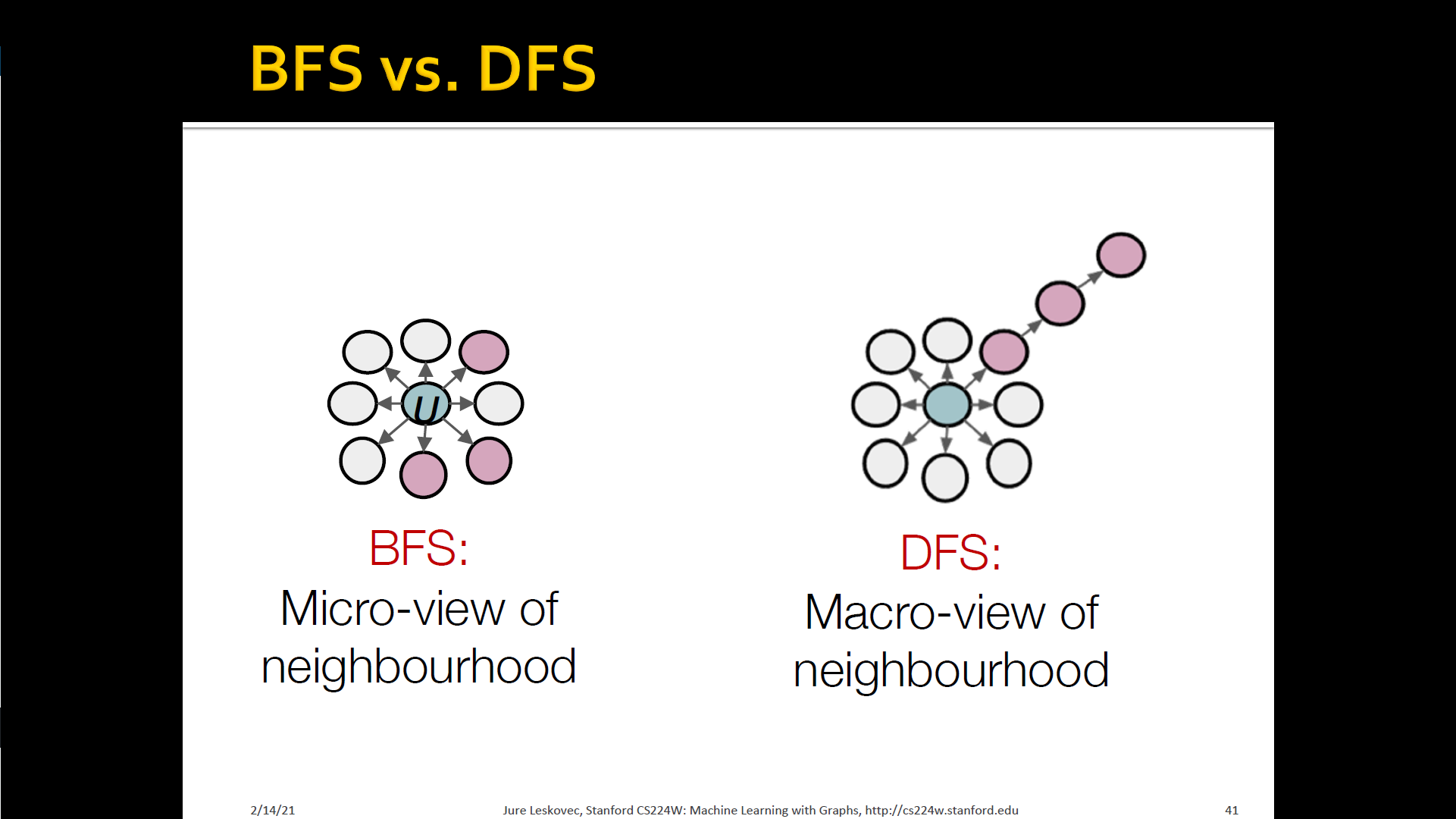
- IDEA: use flexible, biased random walks that can trade-off b/t local and global vies of the network
-
Interpolating BFS and DFS
- Biased fixed-length random walk that given a node generates neighborhood
- Two parameters
- Return parameter : Return back to the previous node
- In-out parameter : Moving outwards(DFS) vs. Inwards(BFS)
- Intuitively, is the "ratio" of DFS vs. BFS
- Two parameters
- Biased fixed-length random walk that given a node generates neighborhood
-
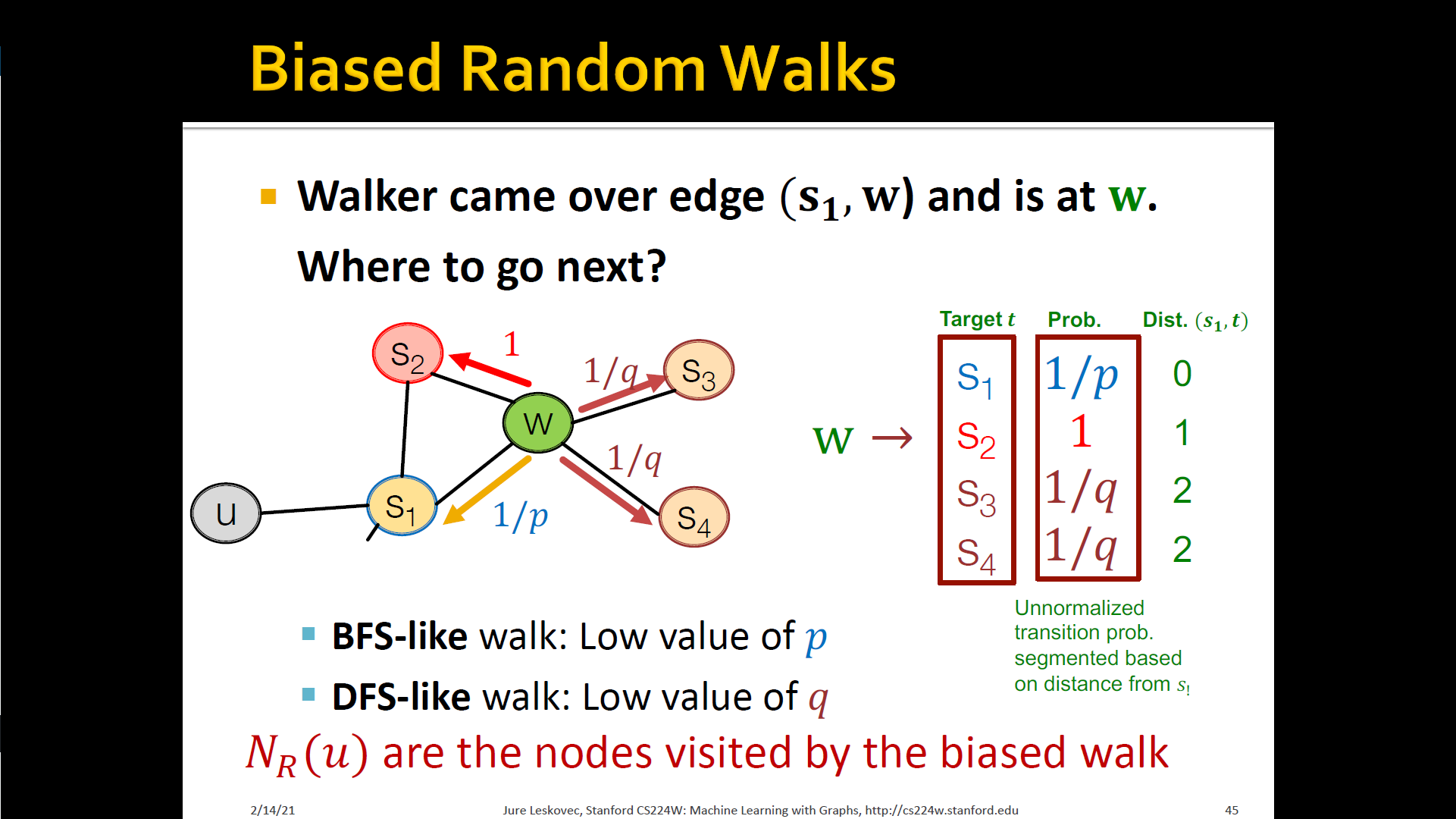
Biased random walks
- Node2Vec algorihthm
- Compute random walk probabilities
- Simulate random walks of length starting from each node
- Optimize the Node2Vec objective using Stochastic Gradient Descent
- Linear-time complexity
- All 3 steps are individually parallelizable
- Other random walk ideas
- Different kinds of biased random walks
- Alternative optimization schemes
- Network pre-processing techniques
Summary
3.3 Embedding entire graphs
- Graph embedding : Want to embed a subgraph or an entire graph
- Tasks
- Classifying toxic vs. non-toxic molecules
- Identifying anomalous graphs
- Approach 1
- Run a standard node embedding technique on the (sub) graph
- Then just sum (or average) the node embeddings in the (sub) graph
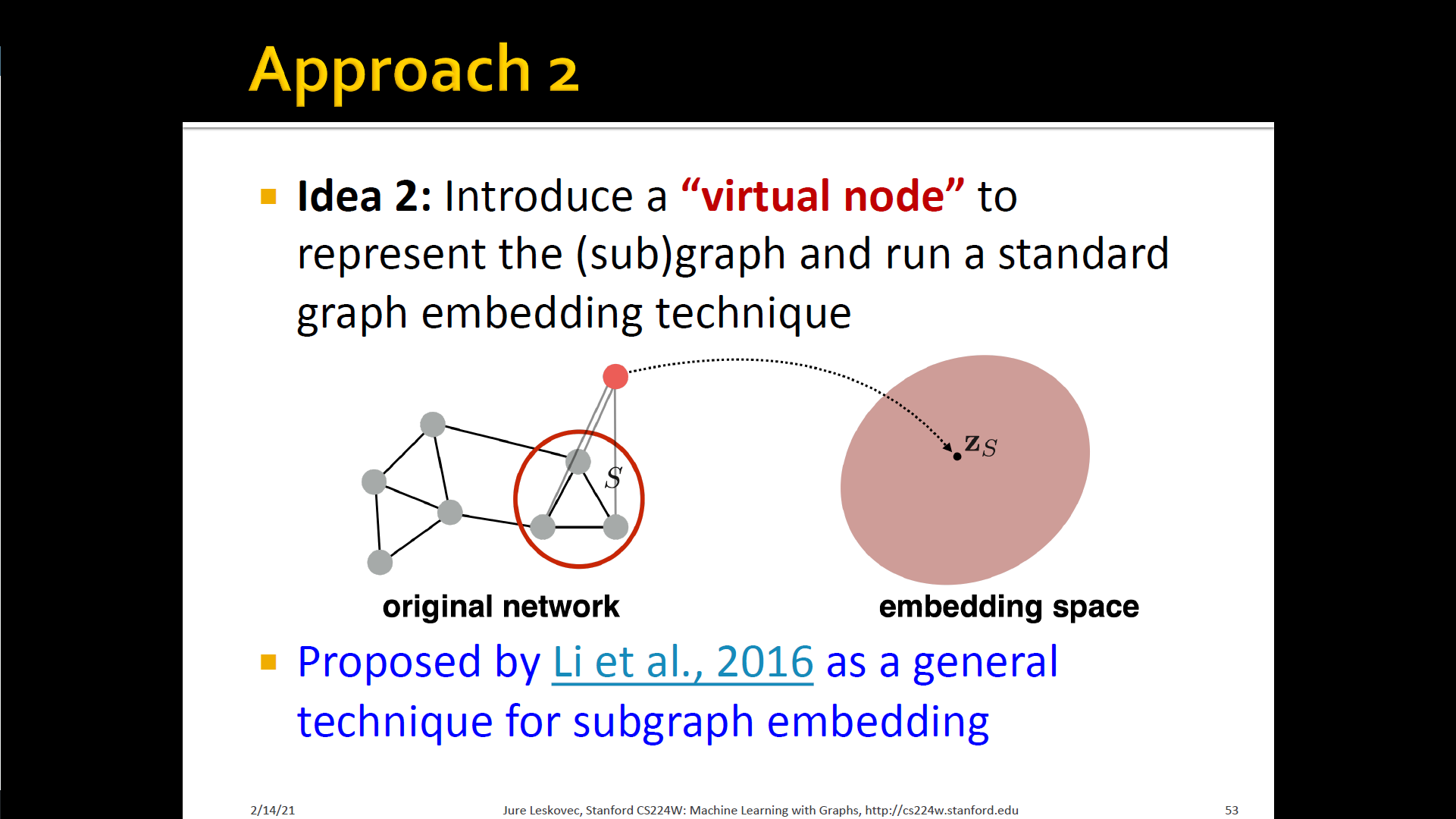
- Approach 2
- Introduce a "virtual node" to represent the (sub) grpah and run a standard node embedding technique

- Introduce a "virtual node" to represent the (sub) grpah and run a standard node embedding technique
-
Approach 3 : Anonymous walk embeddings
- States in anonymous walks correspond to the index of the first time we visited the node in a random walk


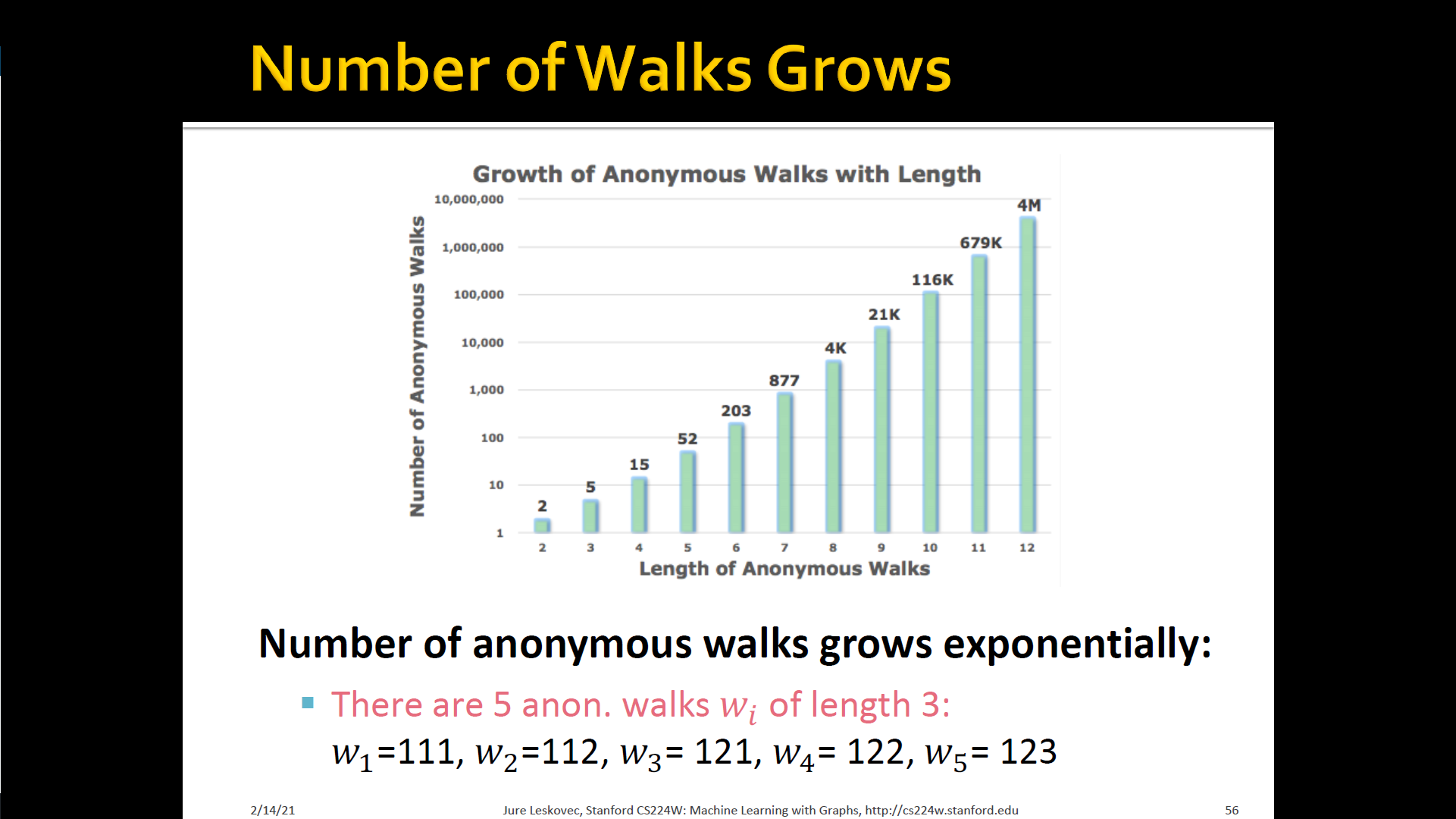


- States in anonymous walks correspond to the index of the first time we visited the node in a random walk
-
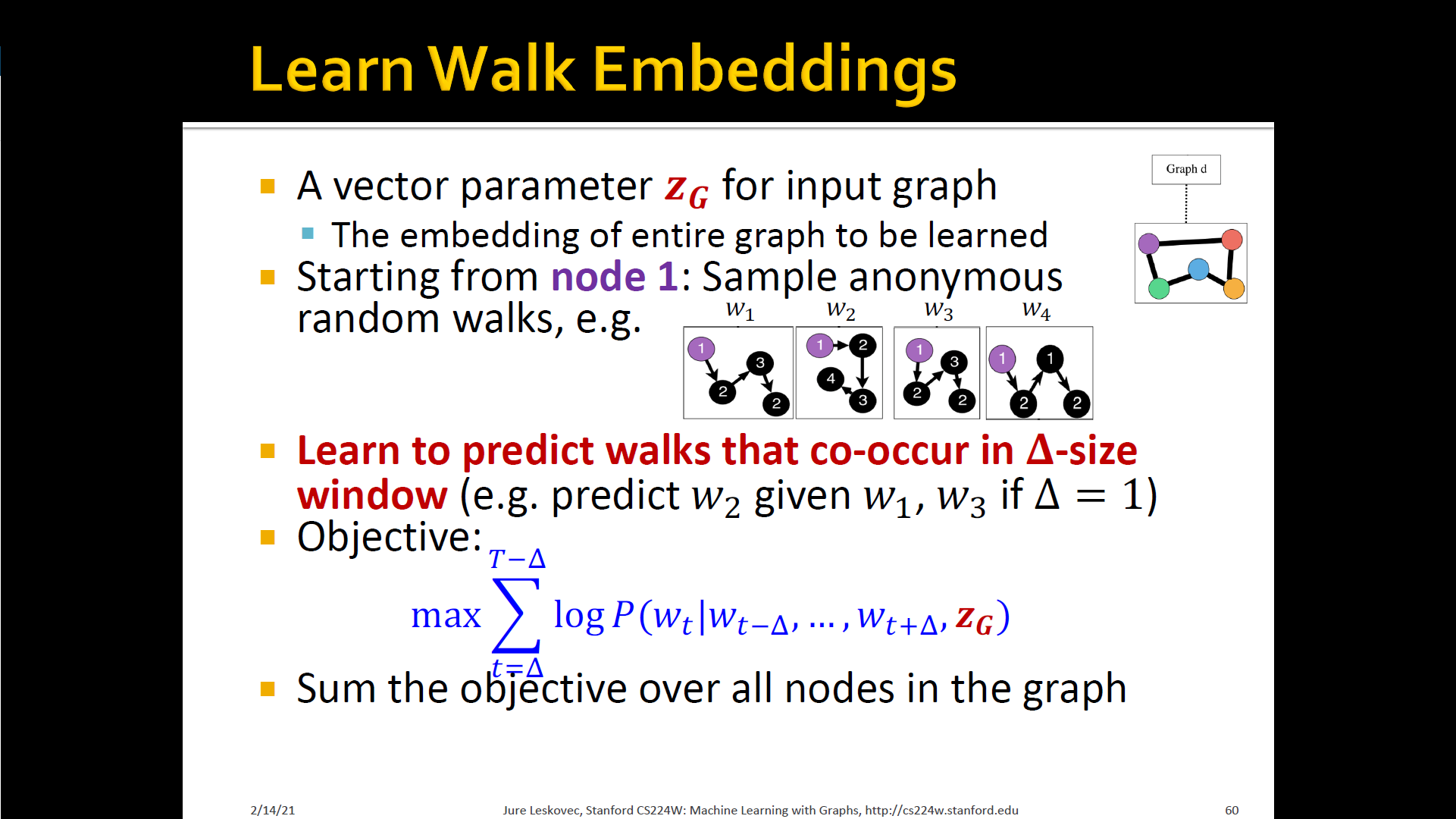
New idea: Learn walk embeddings
- Rather than simply represent each walk by the fraction of times it occurs, we learn embedding of anonymous walk
- Learn a graph embedding together with all the anonymous walk embeddings . , where is the number of sampled anonymous walks
- How to embed walks? Embed walks s.t. the next walk can be predicted

Summary
- How to use embeddings
- Clustering/community detection: cluster points
- Node classification: Predict label of node based on
- Link prediction: Predict edge based on
- Where we can: concatenate, avg, product, or take a difference b/t the embeddings
- Graph classification: graph embedding via aggregating node embeddings or anonymous random walks → Predict label based on graph embdding
Summary