Traditional Methods for ML in Graphs

Sirius·2023년 9월 10일

[GNN] CS224W : ML with Graphs

목록 보기

2/3

Traditional methods for machine learning in graphs

The goal of lecture: Creating additional features that will describe how this particular node is positioned in the rest of the network and what is its local network structure
- These additional features that describe the topology of the network of the graph will allow us to make more accurate predictions
- Using effective features over graphs is the key to achieving good test performance
ML in Graphs
- Given
  $G = (V, E)$
- Learn a function
  $f: V -> \R$
- The way we can think of this is that we are given a graph as a set of verticies, as a set of edges and we wanna learn a function

2.1 Node-level tasks and features

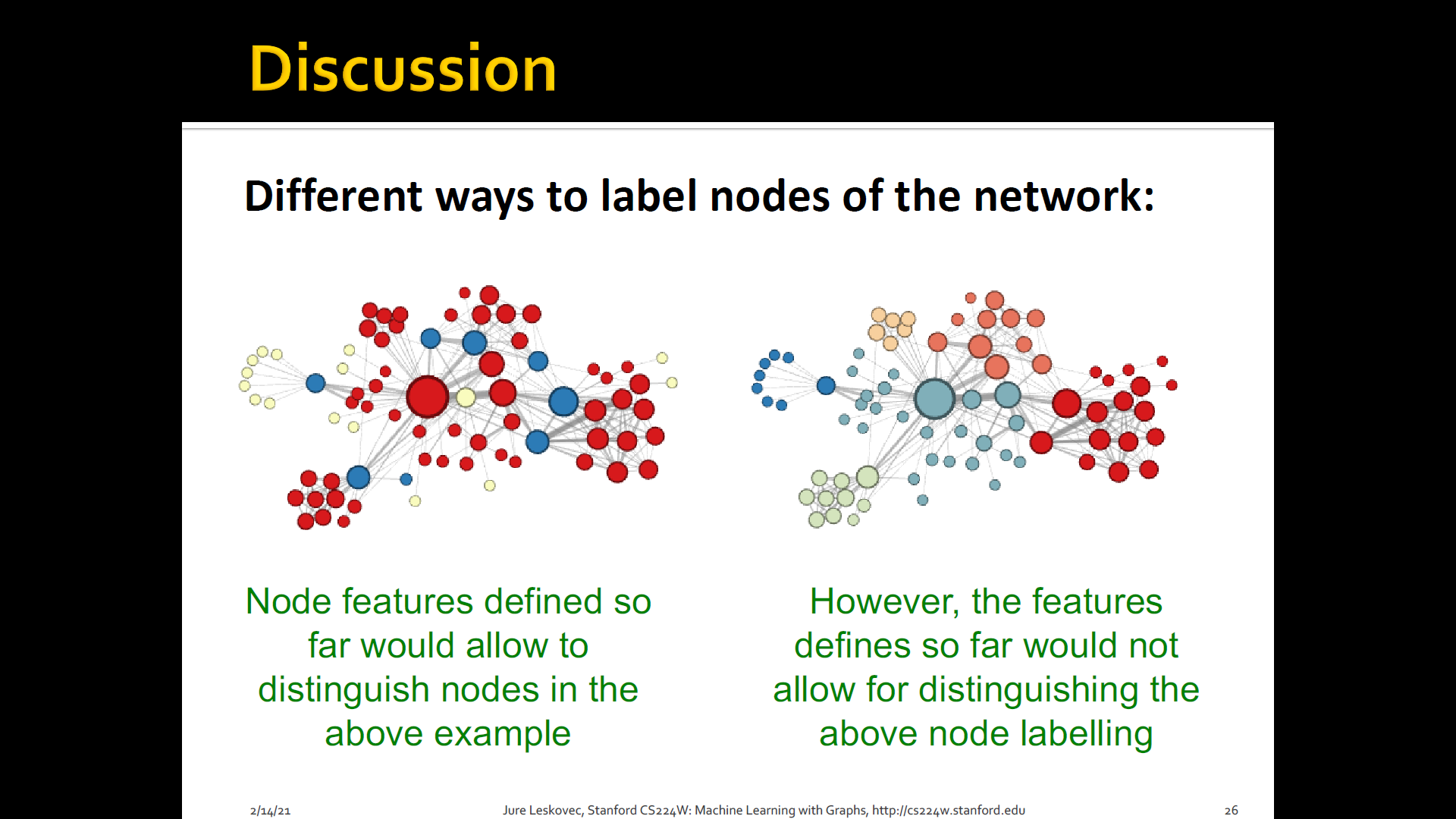
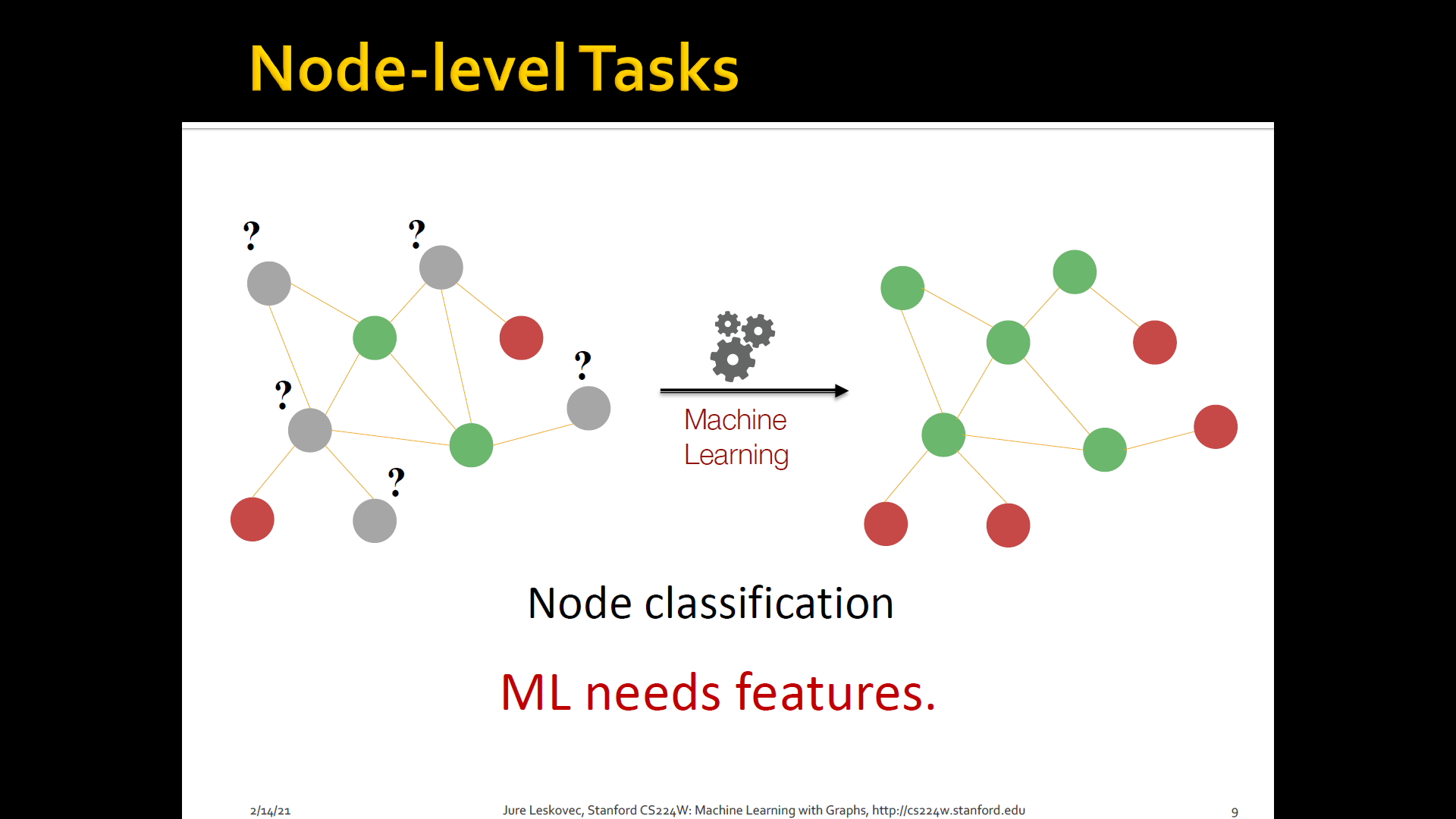
Node classification: Where we are given a network, we are given a couple of nodes that are labeld with different colors, and the goal is to predict the colors of uncolored nodes
Goal: Characterize the structure and position of a node in the network
- Node degree
- Node centrality
- Clustering coefficient
- Graphlets

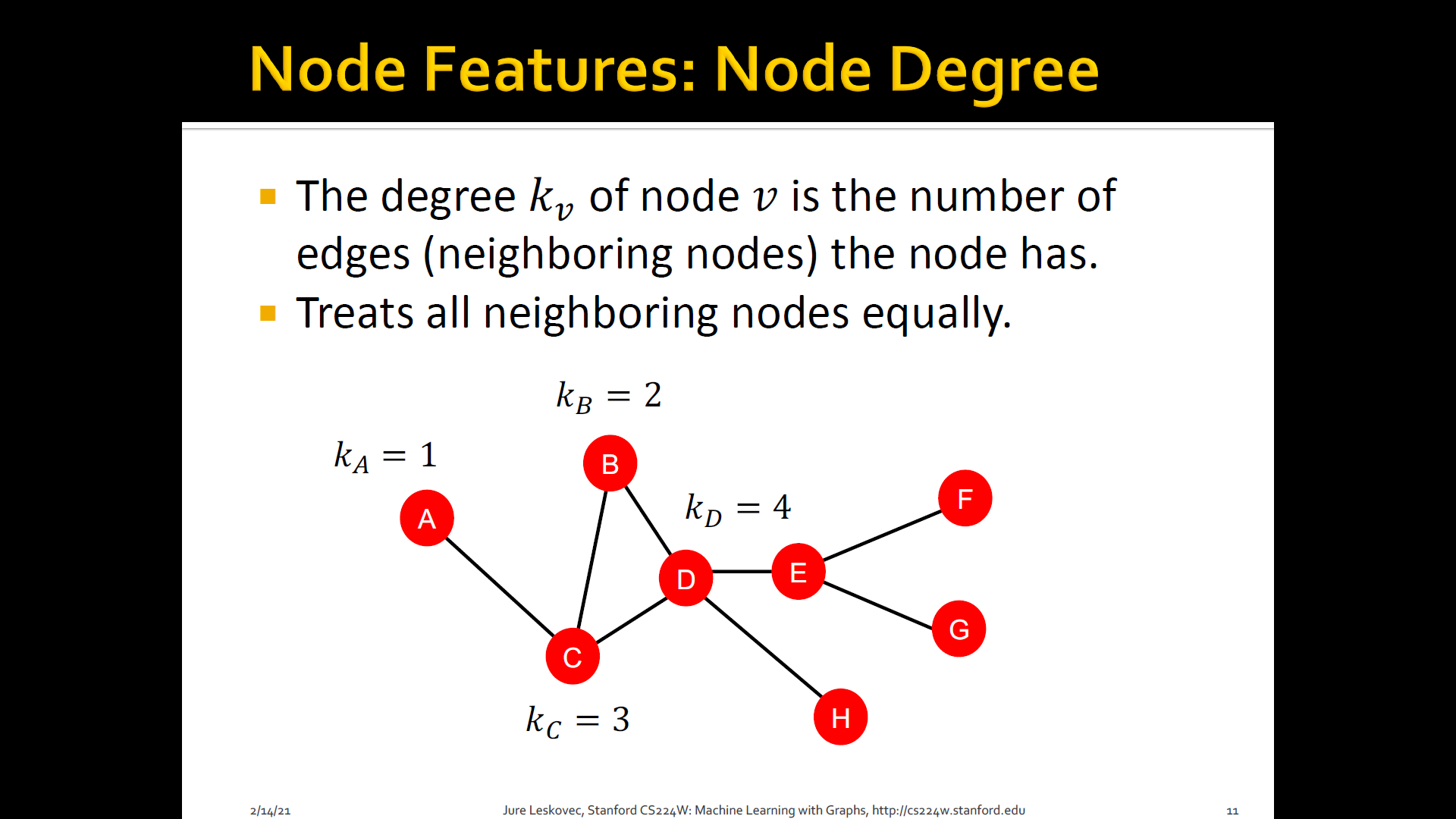
1. Node degree

The degree of $k_v$ of $node \, v$ is the number of edges (neighboring nodes) the node has
Treats all neighboring nodes equally

2. Node centrality

Node degree counts the neighboring nodes without capturing their importance
Node centrality $c_v$ takes the node importance in a graph into account
Different ways to model importance
- Eigen-vector centrality
- Betweenness centrality
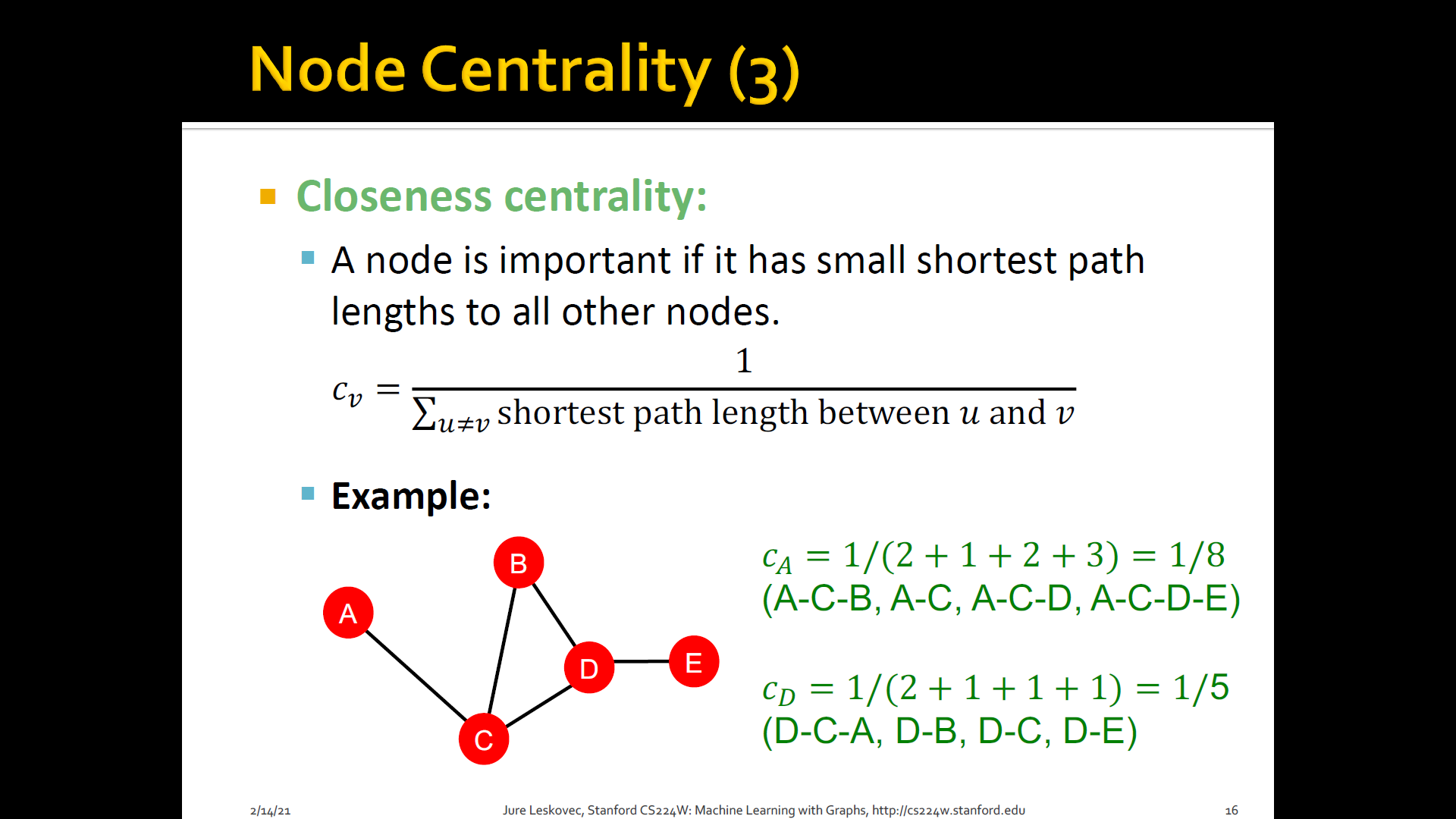
- Closeness centrality
- and many others
Eigen-vector centrality: A node $v$ is important if surrounded by important neighboring nodes $u \in N(v)$
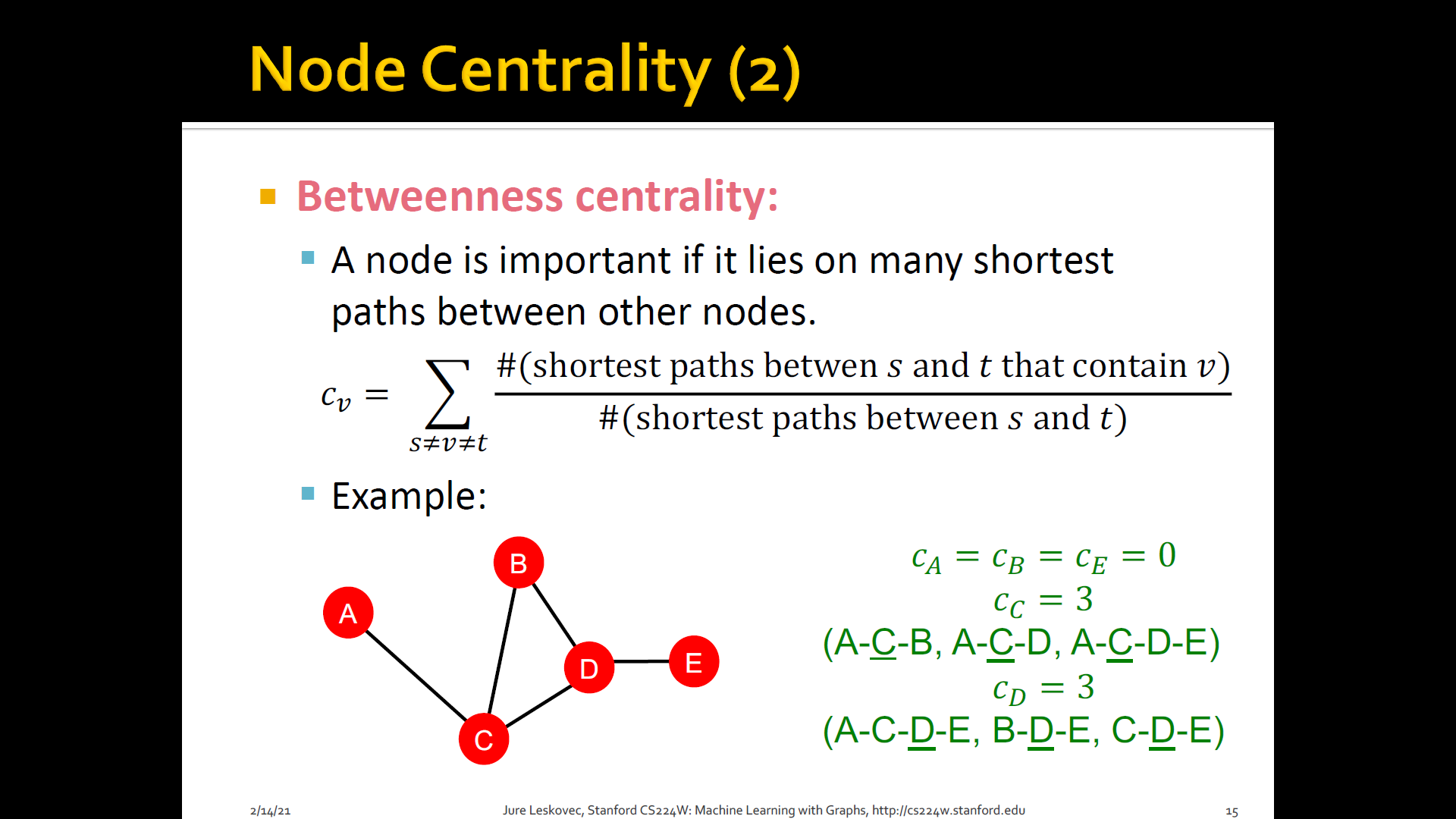
Betweenness centrality: A node $v$ is important if it lies on many shortest paths b/t other nodes
Closeness centrality: A node $v$ is important if it has small shortest path lengths to all other nodes

3. Clustering coefficient

4. Graphlets

Observation: Clustering coeffieicnt counts the #(triangles) in the ego-network
We can generalize the by #(pre-specified subgraphs, i.e. graphlets)
Graphlets: Rooted connected non-isomorphic subgraphs
GDV(Graphlet Degree Vector): Graphlet-base features for nodes
- Degree counts #(edges) that a node touches
- Clustering coefficient counts #(triangles) that a node touches
- GDV counts #(graphlets) that a node touches
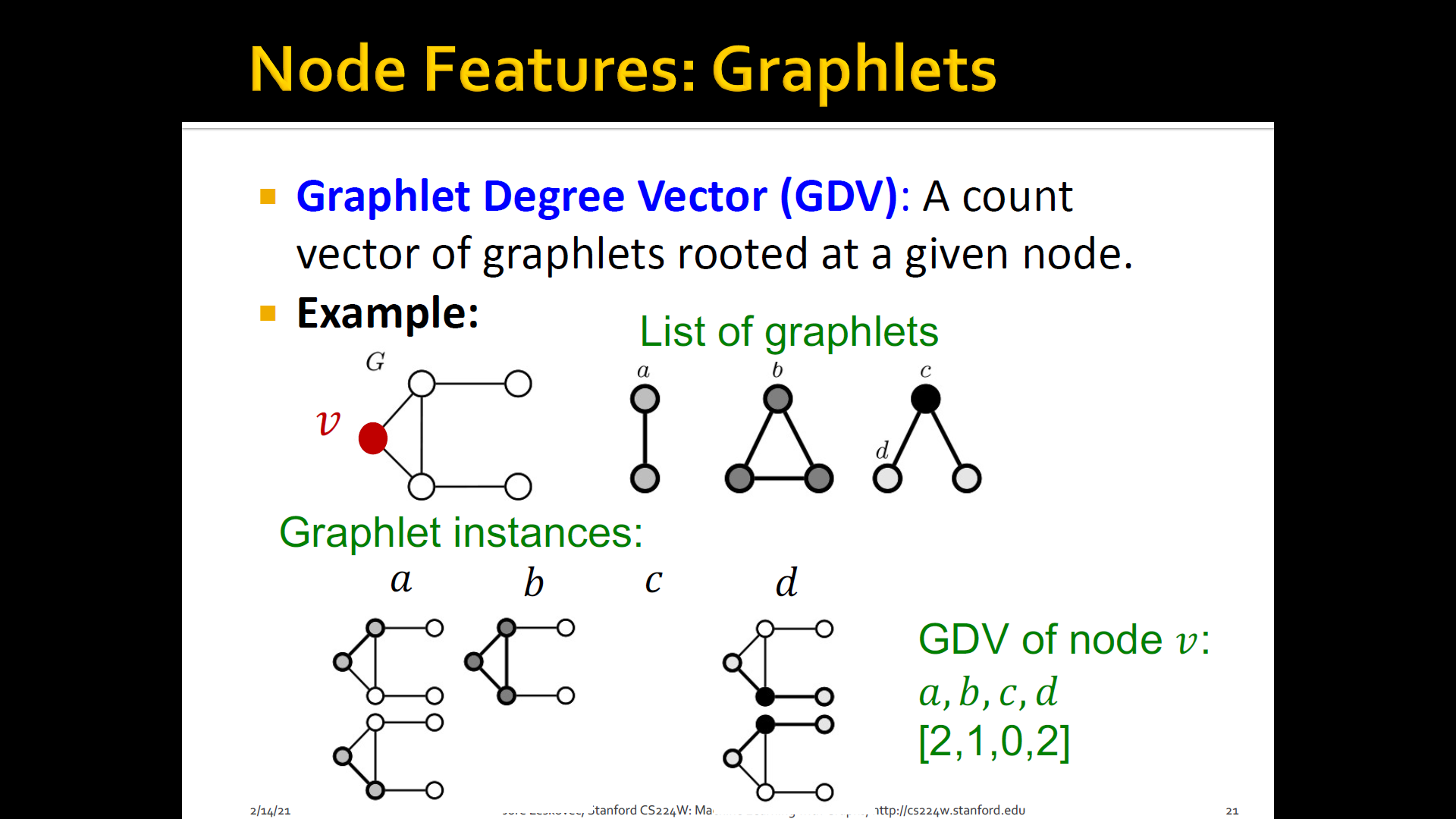
GDV(Graphlet Degree Vector): A count vector of graphlets rooted at a given node
Considering graphlets on 2 to 5 nodes we get:
- Vector of 73 coordinates is a signature of a node that describes the topology of node's neighborhood
- Captures its inter-connectivities out to a distance of 4 hops
Graphlet degree vector provides a measure of a node's local network topology:
- Comparing vectors of two nodes provides a more detailed measure of local topological similarity than node degrees or clustering coefficient

Summary

2.2 Link prediction task and features

The link prediction task is to predict new links based on existing links
At test time, all node pairs(no existing links) are ranked, and top $k$ node pairs are predicted
The key is to design features for a pair of nodes
Two formulations of the link prediction task
- Links missing at random
  - Remove a random set of links and then aim to predict them
  - More useful for static networks like protein-protein interaction networks
- Links over time
- Given $G[t_0, t'_0]$ a graph on edges up to time $t'_0$ , output a ranked list $L$ of links (not in $G[t_0, t'_0]$ ) that are predicted to appear in $G[t_1, t'_1]$
- Evaluation
  - $n=|E_{NEW}|$ : # new edges that appear during the test period $[t_1, t'_1]$
  - Take top $n$ elements of $L$ and count correct edges
  - Useful or natural for networks that evolve over time like transaction networks, social networks
Methodology
- For each pair of nodes $(x, y)$ compute score $c(x, y)$
- For example, $c(x, y)$ could be the # of common neighbors of $x$ and $y$
- Sort pairs $(x, y)$ by the decreasing score $c(x, y)$
- Predict top $n$ pairs as new links
- See which of these links actually appear in $G[t_1, t'_1]$
Link-level features:
- How to featurize or create a descriptor of the relationship b/t two nodes in the network
- Distance-based feature
- Local neighborhood overlap
- Global neighborhood overlap

1. Distance-based features

Shortest path distance b/t two nodes
However, this does not capture the degree of neighborhood overlap(=strength of connection)

2. Local neighborhood overlap

Try to capture the strength of connection b/t two nodes would be to ask how many neighbors do you have in common
What is the number of common friends b/t a pair of nodes
Captures # neighboring nodes shared b/t two nodes $v_1$ and $v_2$
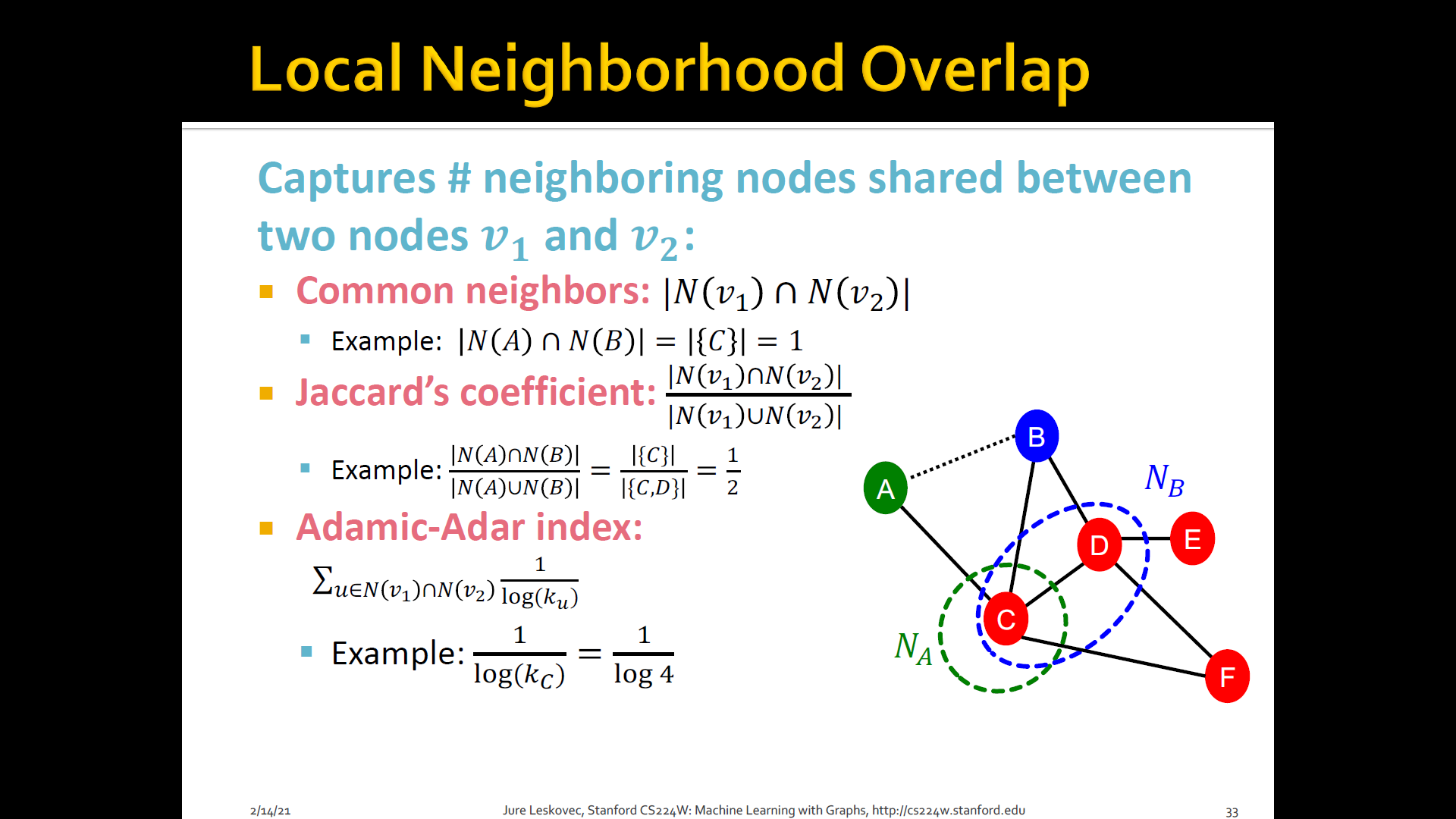
Limitation: Is always zero if the two nodes do not have any neighbors in common (However, the two nodes may still potentially be connected in the future)

3. Global neighborhood overlap

Resolve the limitation of local neighborhood overlap by considering the entire graph
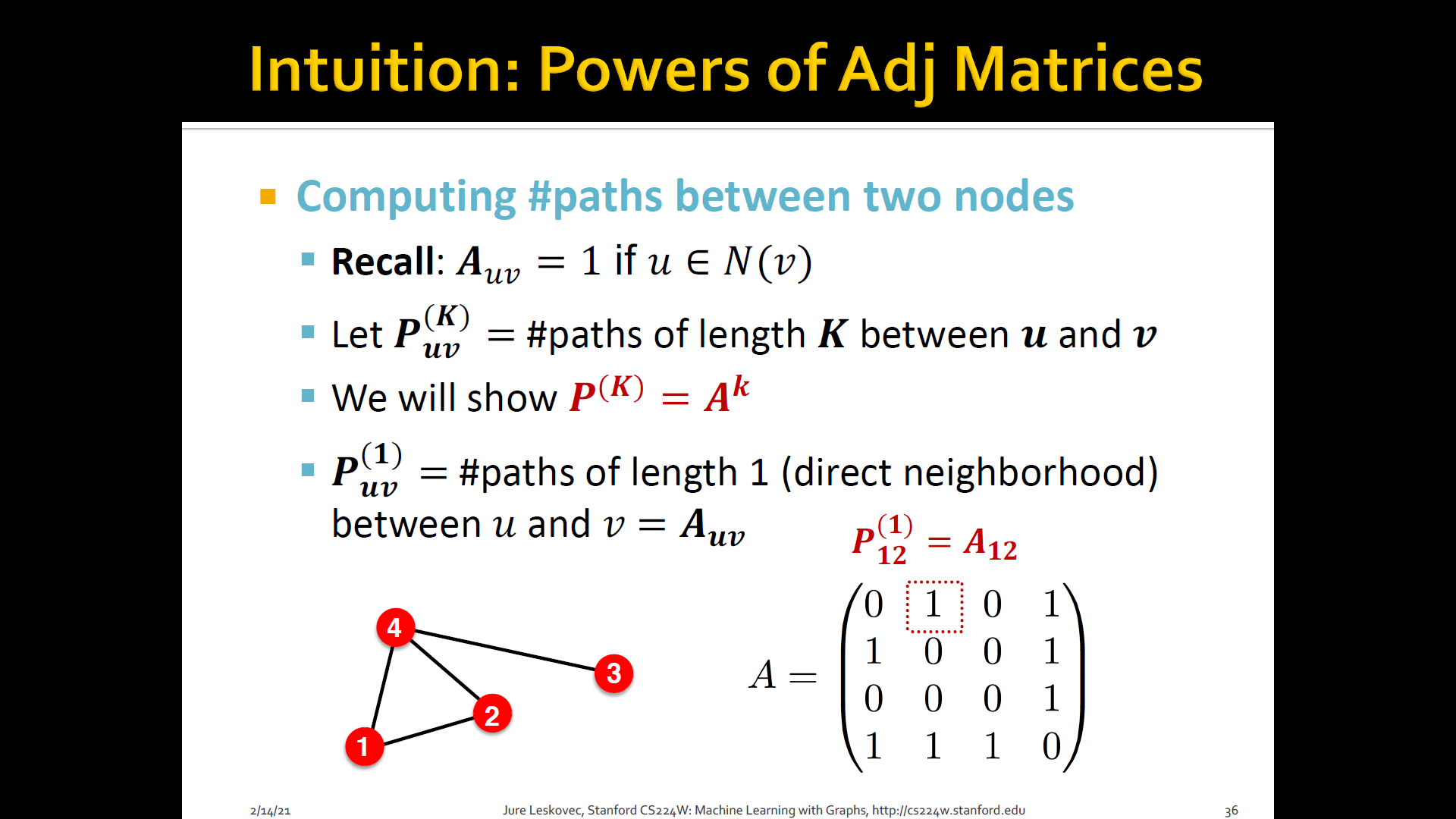
Katz index: count the number of paths of all lengths b/t a given pair of nodes
- How to compute # paths b/t two nodes?
- Use adjacency matrix

Summary

2.3 Graph-level features and Graph kernels

Features that characterize the structure of an entire graph
Kernel methods are widely-used for traditional ML for graph-level prediction
- IDEA: Design kernels instead of feature vectors
- A quick introduction to Kernels
  - Kernel $K(G, G') \in \R$ measures similarity b/t data
  - Kernel matrix $K=(K(G, G'))_{G, G'}$ must always be positive semi-definite (i.e., has positive eigenvalues)
  - There exists a feature representation $\phi(\cdot)$ such that $K=(G, G')=\phi(G)^T\phi(G')$
    - And the value of the kernel is simply a dot product of this vector representation of the two graphs
    - Once the kernel is defined, off-the-shelf ML model, such as kernel SVM can be used to make predictions
Graph Kernels: Measure similarity b/t two graphs
- Goal: Design graph feature vector $\phi(G)$
- Key IDEA: BoW(Bag-of-Words) for a graph
  - BoW simply uses the word counts as features for documents (no ordering considered)
[1] Graphlet kernel
[2] WL(Weisfeiler-Lehman) kernel
[3] Other kernels are also proposed in the literature
- Random-walk kernel
- Shortest-path graph kernel
- And many more
Both Graphlet kernel and WL kernel use Bag-of-* representation of graph, where * is more sophisticated than node degress

1. Graphlet features

Count the number of different graphlets in a graph
Definition of graphlets here is slightly different from node-level features
Two two differences are
- Nodes in graphlets here do not need to be connected (allows for isolated nodes)
- The graphlets here are not rooted
Limitations: Counting graphlet is expensive
Counting size- $k$ graphlets for a graph with size $n$ by enumeration takes $n^k$
This is unavoidable in the worst-case since subgraph isomorphism test (judding whether a graph is a subgraph of another graph) is NP-hard
If a graph's node degree is bounded by $d$ , an $O(nd^{k-1})$ algorithm exists to count all the graphlets of size $k$

2. WL(Weisfeiler-Lehman) Kernel

Goal: Design an efficient graph feature descriptor of $\phi(G)$
IDEA: Use neighborhood structure to iteratively enrich node vocabulary
- Generalized version of Bag-of-node degrees since node degrees are one-hop neighborhood information
- Algorithm to achieve this: WL graph isomorphsim test(=Color refinement)
Color refienment
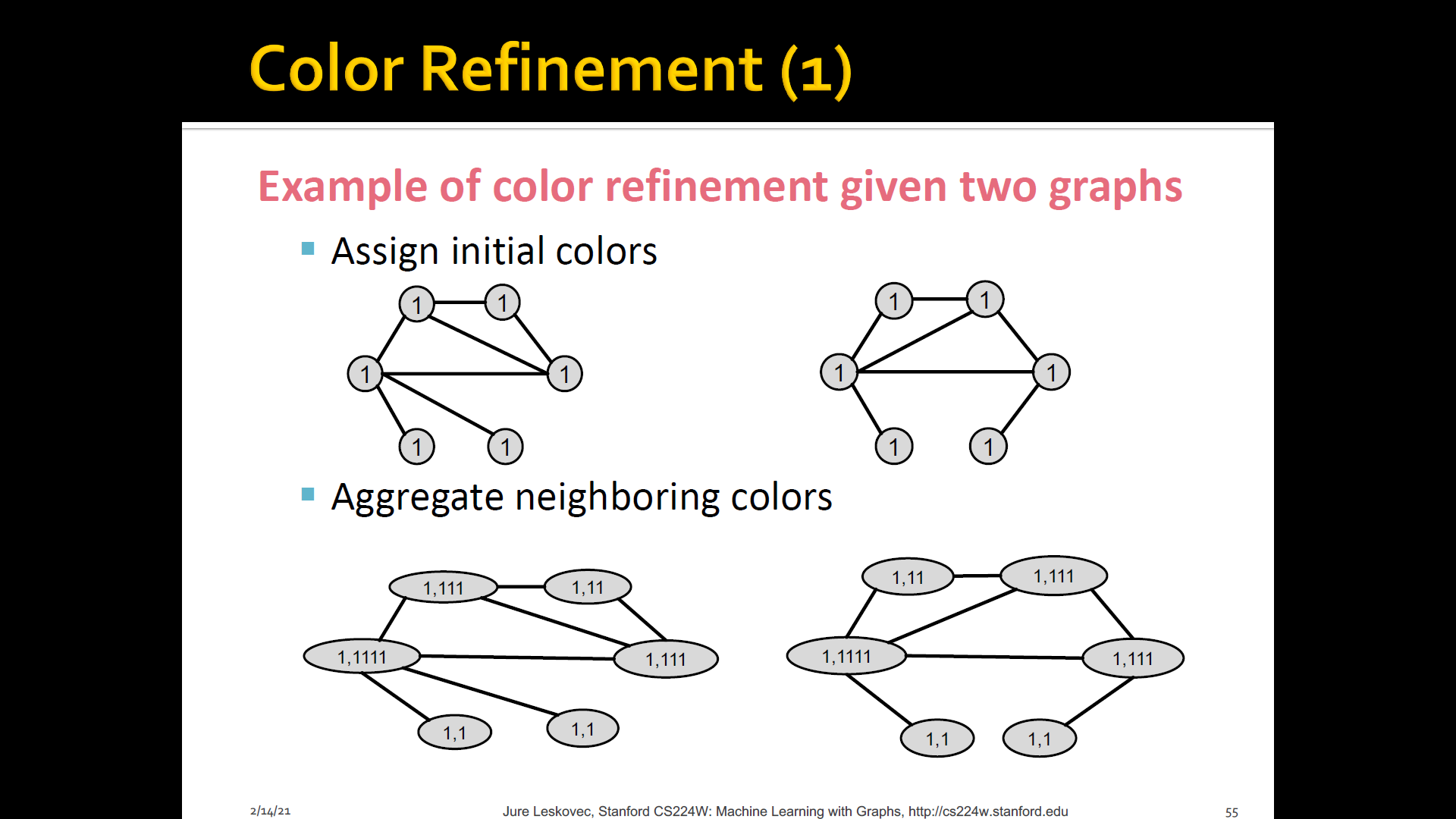
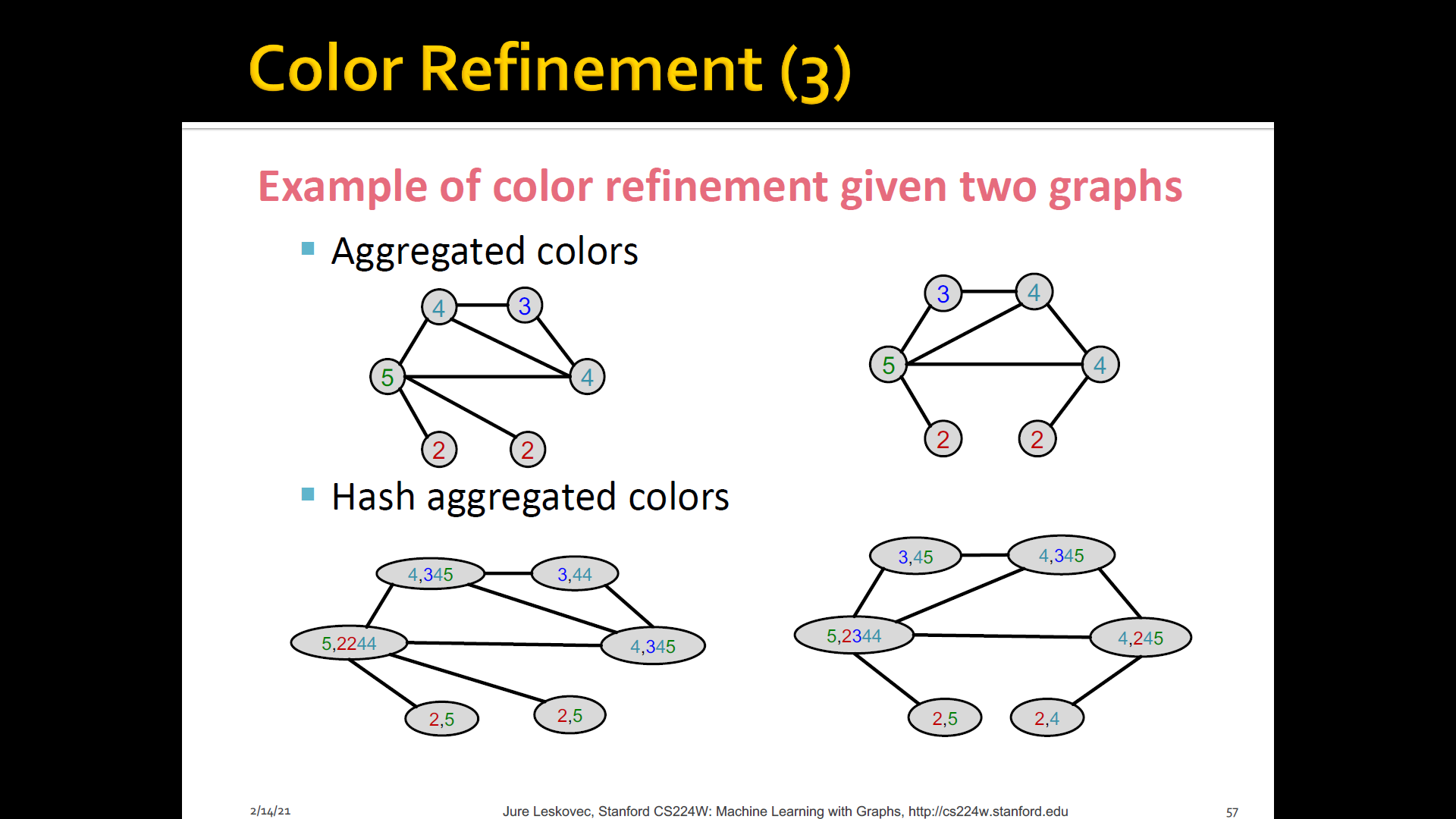
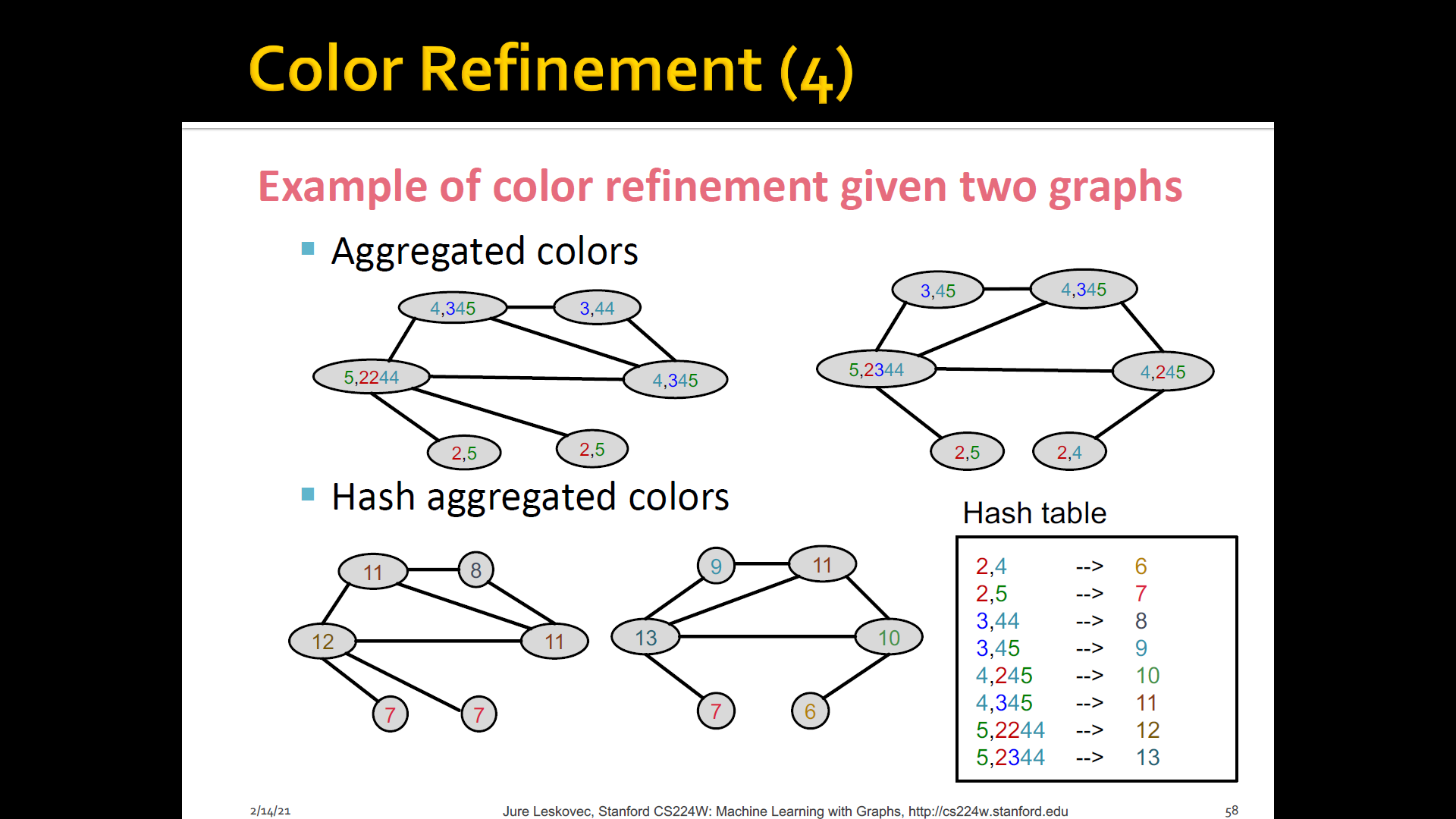
WL kernel is very popular/strong graph feature descriptor to gives strong performance and computationally efficient
- The time complexity for color refinement at each step is linear in #(edges), since it involves aggregating neighboring colors
- When computing a kernel value, only colors appeared in the two graphs need to be tracked
  - Thus, #(colors) is at most the total number of nodes
  - Counting colors takes linear-time w.r.t #(nodes)
  - In total, time complexity is linear in #(edges)