회귀 (Regression)
✅단순 선형 회귀
- 하나의 특징을 가지고 라벨값을 예측하기 위한 회귀모델
- 가장 단순한 모델로 변수들의 관계를 일차식의 형태로 만들어 최적의 a,b 값을 찾아 선을 만듦
- 최적의 a,b 값을 찾기 위해 경사 하강법 이용
1. 데이터 준비를 위해 사이킷런 함수/라이브러리 불러오기
# 데이터 분리 모듈
from sklearn.model_selection import train_test_split
# 사이킷런에 구현되어 있는 회귀 모델 불러오기
from sklearn.linear_model import LinearRegression
2. 데이터 생성 - (load_data())
np.random.seed() 에서 난수 생성 패턴을 동일하게 관리할 수 있음train_test_split(X, y, test_size=0.3, random_state=0): 데이터의 70%를 학습에 사용하고, 나머지 30%의 데이터를 테스트용 데이터로 나눈 결과 데이터를 반환
def load_data():
np.random.seed(0) # random data seed 설정
X = 5*np.random.rand(100,1)
y = 3*X + 5*np.random.rand(100,1)
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.3, random_state=0)
return train_X, test_X, train_y, test_y
3. 단순 선형회귀 - regression_model(train_X, train_y)
from sklearn.linear_model import LinearRegression: 단순 선형 회귀 모델을 불러옴LinearRegression() : 모델을 정의[Model].fit(X, y) : X, y 데이터셋에 대해서 모델을 학습시킴
def regression_model(train_X, train_y):
simplelinear = LinearRegression()
simplelinear.fit(train_X,train_y)
return simplelinear
4. main 함수
- 데이터를 불러와 테스트 데이터에 대한 예측 수행
[Model].predict(X): X 데이터에 대한 예측값을 반환[Model].score(X, y) : 테스트 데이터를 인자로 받아 학습이 완료된 모델의 평가 점수를 출력[Model].intercept_ : 학습이 완료된 모델의 β0 반환[Model].coef_ : 학습이 완료된 모델의 β1 반환
def main():
train_X, test_X, train_y, test_y = load_data()
simplelinear = regression_model(train_X, train_y)
predicted = simplelinear.predict(test_X)
model_score = simplelinear.score(test_X, test_y)
beta_0 = simplelinear.intercept_
beta_1 = simplelinear.coef_
print("> beta_0 : ",beta_0)
print("> beta_1 : ",beta_1)
print("> 모델 평가 점수 :", model_score)
# 시각화 함수 호출하기
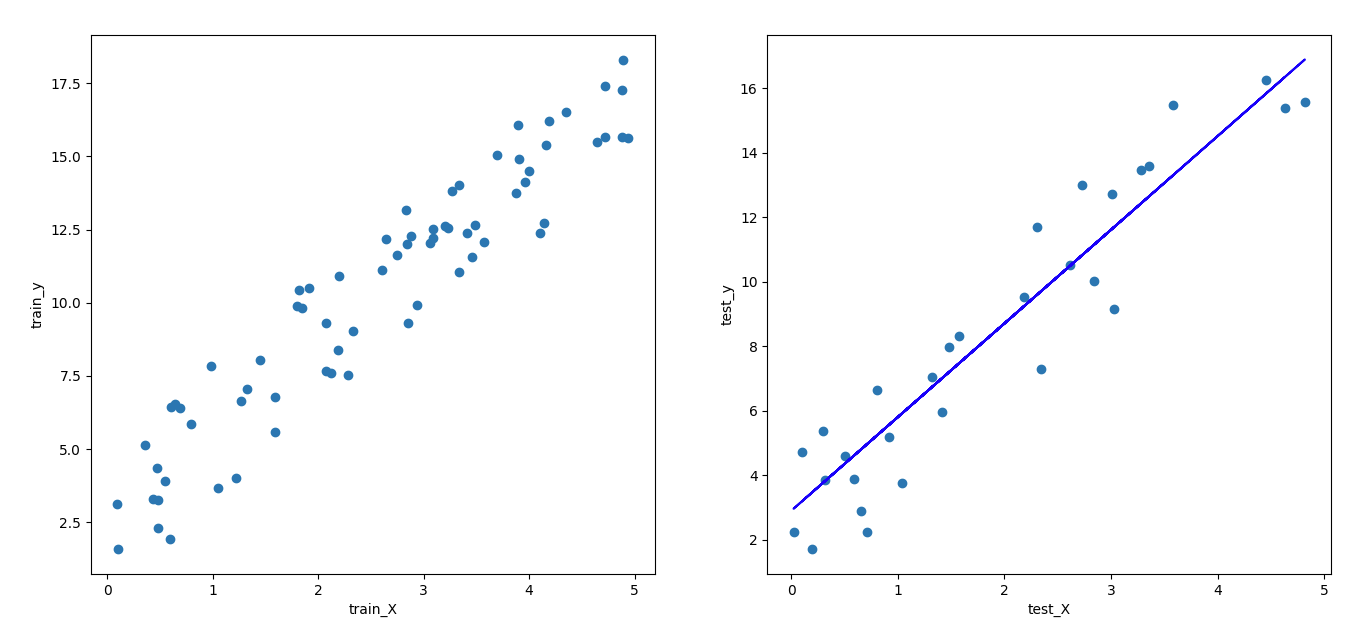
plotting_graph(train_X, test_X, train_y, test_y, predicted)
return predicted, beta_0, beta_1, model_score
✅다중 선형 회귀
- 여러 개의 입력값으로 결과값을 예측하고자 하는 경우
- 어떤 입력값이 결과값에 어떠한 영향을 미치는지 알 수 있음
- 여러 개의 입력값 사이 간 상관관계가 높을 경우 결과에 대한 신뢰성을 잃을 수 있음
1. 데이터 준비를 위한 사이킷런 함수/라이브러리
# 사이킷런의 boston 데이터를 불러옴
from sklearn.datasets import load_boston
# (X, y)형태의 boston 데이터를 반환
load_boston(return_X_y = True)
2. 데이터 생성 - load_data()
- 사이킷런에 존재하는 boston 데이터를 (X,y) 형태로 불러오기
def load_data():
X, y = load_boston(return_X_y=True)
print("데이터의 입력값(X)의 개수 :", X.shape[1])
# 학습용 데이터와 테스트용 데이터로 분리
# 테스트용 데이터로 20% 사용하고 동일 결과 위해 random_state=100 설정
train_X, test_X, train_y, test_y = train_test_split(X,y,test_size=0.2, random_state=100)
return train_X, test_X, train_y, test_y
3. 다중 선형 회귀 - Multi_Regression(train_X, train_y)
LinearRegression() : 다중 선형 회귀 모델을 정의[Model].fit(X, y) : X, y 데이터셋에 대해서 모델을 학습시킴
def Multi_Regression(train_X,train_y):
multilinear = LinearRegression()
multilinear.fit(train_X, train_y)
return multilinear
4. main 함수
- 데이터를 불러와 테스트 데이터에 대한 예측 수행
[Model].predict(X): X 데이터에 대한 예측값을 반환[Model].score(X, y) : 테스트 데이터를 인자로 받아 학습이 완료된 모델의 평가 점수를 출력[Model].intercept_ : 학습이 완료된 모델의 β0 반환[Model].coef_ : 학습이 완료된 모델의 β1 반환 (리스트로 저장됨)
def main():
train_X, test_X, train_y, test_y = load_data()
multilinear = Multi_Regression(train_X,train_y)
predicted = multilinear.predict(test_X)
model_score = multilinear.score(test_X, test_y)
print("\n> 모델 평가 점수 :", model_score)
beta_0 = multilinear.intercept_
beta_i_list = multilinear.coef_
print("\n> beta_0 : ",beta_0)
print("> beta_i_list : ",beta_i_list)
return predicted, beta_0, beta_i_list, model_score
✅다항 회귀
- 다중 선형회귀 적용 시 예측 결과값이 좋지 않고, 데이터들간의 관계가 선형적이지 않은 경우
- 일차 함수 식으로 표현할 수 없는 복잡한 데이터 분포에도 적용 가능
- 극단적으로 높은 차수의 모델을 구현할 경우 과도하게 학습 데이터에 맞춰지는 과적합 현상 발생
- 다중 선형 회귀와 동일한 원리
1. 데이터 준비를 위한 사이킷런 함수/라이브러리
PolynomialFeatures(degree, include_bias) : Polynomial 객체를 생성
degree : 만들어줄 다항식의 차수include_bias : 편향 변수의 추가 여부 설정 (True/False), True로 설정하게 되면 해당 다항식의 모든 거듭제곱이 0일 경우 편향 변수를 추가. 이는 회귀식에서 β0과 같은 역할
2. 데이터 생성 -load_data()
def load_data():
np.random.seed(0)
X = 3*np.random.rand(50, 1) + 1
y = X**2 + X + 2 +5*np.random.rand(50,1)
return X, y
Polynomial 객체 생성[PolynomialFeatures].fit_transform(X) : 변수 값을 제곱하고 이를 X에 추가시킨 후 poly_X에 저장 fix(X)와 transform(X)를 각각 분리해서 진행하는 것도 가능
def Polynomial_transform(X):
poly_feat = PolynomialFeatures(degree=2, include_bias=True)
poly_X = poly_feat.fit_transform(X)
print("변환 이후 X 데이터\n",poly_X[:3])
return poly_X
4. 다중 선형 회귀 - Multi_Regression(poly_x, y)
LinearRegression() : 다중 선형 회귀 모델을 정의[Model].fit(X, y) : X, y 데이터셋에 대해서 모델을 학습시킴
def Multi_Regression(train_X,train_y):
multilinear = LinearRegression()
multilinear.fit(poly_x, y)
return multilinear
5. main 함수
def main():
X,y = load_data()
poly_x = Polynomial_transform(X)
linear_model = Multi_Regression(poly_x,y)
predicted = linear_model.predict(poly_x)
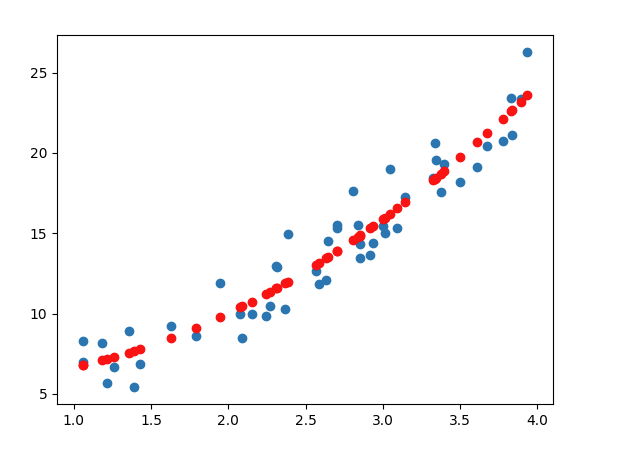
plotting_graph(X,y,predicted)
return predicted
Reference


