[논문 정리] An Efficient Explanation of Individual Classification using Game Theory

thingsu·2022년 9월 4일

XAI shapely value

XAI_papers

목록 보기

1/1

이번에 소개할 논문은 “An Efficient Explanation of Individual Classification using Game Theory”입니다.

많이 알려진 SHAP은 Feature Importance를 계산하기 위해서 shapely value의 개념을 사용합니다.

본 논문은 그 이전에 shapely value를 활용한 explanation method를 제안하는 논문입니다.

논문 링크 : https://dl.acm.org/doi/abs/10.5555/1756006.1756007

Introduction

본 논문은 shapely value를 활용한 explanation을 설명하기 위해서 4 단계로 진행됩니다.

Coaltional Game Theory의 개념을 도입했을 때 기존 Explanation의 한계를 개선할 수 있다.
위의 세팅에서 Feature Importance는 Shapely value로 계산될 수 있다.
Alternative form과 sampling 기법을 통해 적당한 시간 복잡도로 shapely value를 계산할 수 있다.
Feature Contribution을 통해 Instance level에서 모델을 이해하고 신뢰성을 비교할 수 있다.

Explaination & Coal Gameme Theory.

1. Explanation?

Explanation은 모델의 예측을 이해하기 쉽게하고, 신뢰할 수 있게 하기 위해서 필요합니다.
본 논문에서는 모델의 종류와 무관하게 적용될 수 있는 General Explanation
그리고 각 데이터의 prediction에 대해서 instance level의 Explanation을 따릅니다.
따라서 Explanation은 Prediction에 대한 각 Feature의 Contribution을 제시하는 방식으로 이뤄집니다.

2. Coalitional Game Theory?

Game Theory는 player가 협력적인 경우와 비협력적인 경우로 나눌 수 있습니다.
그 중 Coalitional Game은 각 player가 연합(Coalition)해 value를 payoff로 배분하는 형태의 게임입니다.
Shapely Value는 Coalitional Game에서 value를 각 Player에게 동등한(symmetric) contribution을 가정하고 분배하는 payoff를 계산하는 식입니다.

\displaystyle Sh_i(v) = \sum_{S\subseteq{N}\setminus{\{i\}}, s=\left|{S}\right|}\frac{(n-s-1)!}{n!}(v(S\cup{\{i\}})-v(S))

사진 (개념 대응되는)

3. Coalitional Game to Explanation

Coaltional Game의 setting을 아래와 같이 설정한다면 Feature Importance를 계산하는 문제에 적용할 수 있습니다.

player : Feature
value function: set of player → prediction difference
payoff : 각 변수의 contribution

기존의 general explanation 기법은 변수 1개 단위로 다루어 feature간의
conditional dependent한 경우 즉 Interaction을 설명하지 못하는 한계가 있었습니다.

Coaltional Game Theory의 value function은 player의 subset에 대해 값을 부여합니다.
따라서 player에서 player의 set으로 value 계산의 단위를 변경해 변수들의 Interaction을 다룰 수 있을 것입니다.

Define Explanation method

Definitions

(Prediction\,Difference)\, \Delta (S) = \frac{1}{\left|{\mathcal{A}_{{N}\setminus{S}}}\right|} \sum_{{y\in\mathcal{A}_{{N}\setminus{S}}}} f_C(\tau(x,y,S))- \frac{1}{\left|{\mathcal{A}_{N}}\right|} \sum_{{y\in\mathcal{A}_{N}}}f_C(y) \cdots (1)

Prediction Difference은 S에 속한 feature값을 알 때 Prediction 기댓값과 모를 때의 Prediction 기댓값의 차이로 정의했다. 변수들이 Prediction에 평균적으로 미친 영향력을 의미한다.

(Interaction)\, \Delta(S) = \sum_{W \subseteq S}I(W) \:\leftrightarrows\: I(S) = \sum_{W \subseteq S}((-1)^{\left|S\right| - \left|W\right|}\Delta(Q)) \cdots (2)

Prediction Difference는 변수들의 집합 S에서 발생할 수 있는 모든 Interaction의 합으로 정의된다. 왼쪽 식을 귀납적으로 정리하면 오른쪽 식으로 변환할 수 있다.

(i^{th}\,feature's \,Contribution)\, \varphi_i(\Delta) = \sum_{W \subseteq N \setminus\{i\}}\frac{I(W\cup\{i\})}{\left| W\cup \{i\}\right|} \cdots (3)

따라서 i번째 변수의 Contribution은 변수가 포함된 모든 Interaction에서 동등한 contribution을 했음을 가정해 변수 개수로 나눠준 값의 합으로 정의된다. Interaction은 변수 집합의 power set에 대한 값이 아니기 때문에 모든 변수에 동등하게 분배된다는 (symmetric) 가정은 타당하다.

위 식은 다 전체 데이터에 대한(기대값인데) 왜 instance level로 계산이 가능한거지...?

contribution = shapely value

본 논문은 1 페이지 정도의 과정을 통해서 $\varphi_i(\Delta)$ 의 값이 shapely value의 꼴과 같음을 증명합니다.

\varphi_i(\Delta) = \sum_{W \subseteq N \setminus\{i\}}\frac{\sum_{Q \subseteq W \cup\{i\}}((-1)^{\left|W\cup \{i\}\right| - \left|Q\right|}\Delta(Q))}{\left| W\cup \{i\}\right|}

첫째로 (2)식과 (3)식을 연립해 $\Delta(Q)$ 에 관한 식으로 정리합니다.
위 식을 관찰하면 각 subset의 계수는 $\frac{k \choose t}{|S|+1+t}$ 교대급수 꼴임을 알 수 있습니다.

M_{\Delta(S)} \vcentcolon= the\,coefficient\,of\,all\,such\, appearance\,of\,set\,S,\,k = n-|S|-1 \\ M_{\Delta(S\cup\{i\})} = \sum_{t=0}^{k}\frac{-1^{t}}{n-k+t}{k \choose t}=B(n-k,k+1)=V(n,k)\\ M_{\Delta(S)} = \sum_{t=0}^{k}\frac{-1^{t-1}}{n-k+t}{k \choose t}=-B(n-k,k+1)=-V(n,k) \\ \varphi_i(\Delta) = \sum_{S \subseteq N \setminus\{i\}}V(n,k)*(\Delta(S\cup\{i\}) - \Delta(S))

앞선 발견을 수식으로 정리하면 위와 같습니다. 관찰하고자 하는 변수 {i}의 포함 여부에 따라 $\Delta(S\cup\{i\})$ 와 $\Delta(S)$ 두 가지의 계수를 계산했습니다. 따라서 i번째 Feature의 contribution은

\varphi_i(\Delta) = \sum_{S \subseteq N \setminus\{i\}} \frac{(n-s-1)!s!}{n!}(\Delta(S\cup\{i\}) - \Delta(S))

으로 앞서 서술한 shapely value의 꼴과 같습니다.

Example : $1\vee1$

$N=\{1,2\}, \mathcal{A}=\{0,1\}\times\{0,1\}, x=(1,1)$ 인 상황에서
기존의 방법론에서는 $x\vee1$ 은 $1\vee1=0\vee1=1$ 임으로 contribution이 없다.
현재 방법론에서는 아래와 같이 계산됩니다.

$S=\{1\}$
$\Delta(\{1\})=\Delta(\{2\})=\Delta(\{1,2\})=1-\frac{3}{4} = \frac{1}{4}, \Delta(\emptyset)=0$
$\frac{1}{\left|{\mathcal{A}_{{N}\setminus{S}}}\right|} \sum_{{y\in\mathcal{A}_{{N}\setminus{S}}}} f_C(\tau(x,y,S))=\frac{1}{2}*(1+1)$
$\frac{1}{\left|{\mathcal{A}_{N}}\right|} \sum_{{y\in\mathcal{A}_{N}}} f_C(y)=\frac{1}{4}*(1+1+1+0)$
$I(\{1\})=\Delta(\{1\})=\frac{1}{4},\, I(\{2\})=\Delta(\{2\})=\frac{1}{4}$
$I(\{1,2\})=\Delta(\{1,2\})-I(\{1\})-I(\{2\})=-\frac{1}{4}$
$\varphi_1 = I(\{1\})+ \frac{I(\{1,2\})}{2}=\frac{1}{8}, \varphi_2 = I(\{2\})+ \frac{I(\{1,2\})}{2}=\frac{1}{8}$

위 전개를 해보기 전에는 왜 instance별로 다른 결과가 나올 수 있는지 이해하지 못했었는데, instance별로 $f_C$ 에서 다른 값을 가지게 되어 다른 결과가 나오는 것을 확인할 수 있었습니다.

Approximation to calculate features’ contributions

exponential time complexity

\varphi_i(\Delta) = \frac{1}{n!}\sum_{O\in\pi(N)}(\Delta(Pre^{i}(O)\cup\{i\})-\Delta(Pre^{i}(O)))

Shapely Value는 위의 alternative 한 form으로 계산이 가능합니다. Feature contribution을 계산하기 위해선 모든 subset S에 대한 $\Delta$ 계산이 필요합니다. $f_C(\tau(x,y,S))$ 항에서 각 S마다 새로운 모델 학습이 필요하기 때문에 exponential time complexity 문제가 발생합니다.

extend sampling method

미완

min sample to keep error rate and speed

미완

Examples of Explanation

Feature's Contribution

magitude와 sign 두 가지 관점에서 contribution을 해석할 수 있다. magnitude는 prediction에 영향을 미치는 정도 차이이고, sign의 부호에 따라 output을 증가시키거나 감소시키는 영향을 미친다.

Example

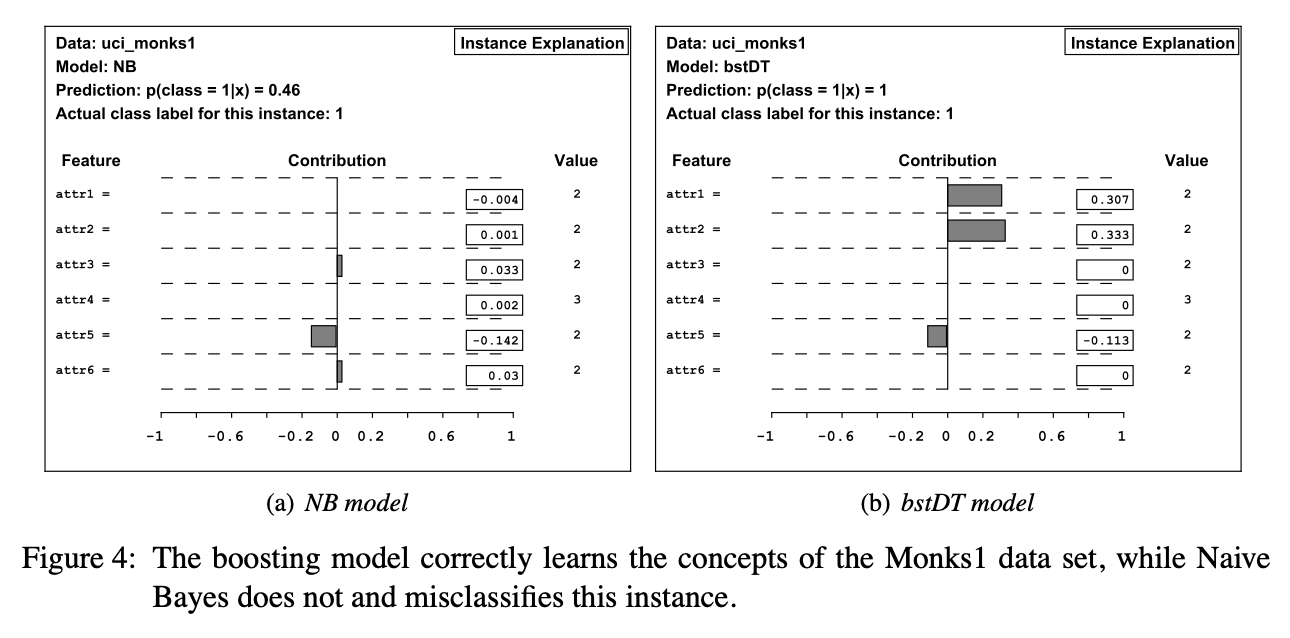
ucl_monks1 dataset의 class 1은 attr1과 attr2가 같거나, attr5=1인 특징이 있습니다. NB model은 bstDT model에 비해 첫번째 특징을 잘 학습하지 못한 것을 확인할 수 있습니다.

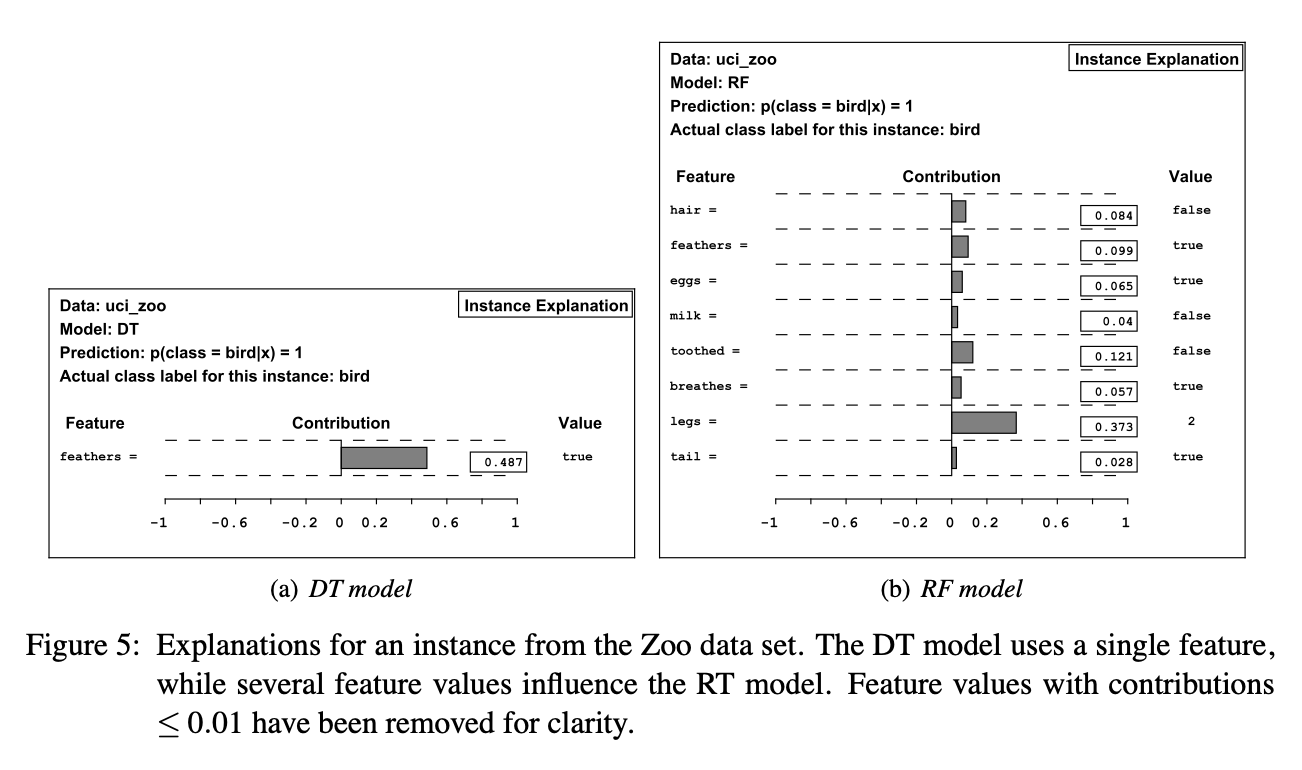
두 모델은 Prediction 항을 보면 같은 예측을 했지만, 판단 근거가 달랐음을 알 수 있습니다. 더 새와 연관된 다양한 feature를 기반으로 예측한 RF 모델이 보다 신뢰성이 높은 모델입니다.