※ Notification
본 포스팅은 작성자가 이해한 내용을 바탕으로 작성된 글이기 때문에 틀린 부분이 있을 수 있습니다.
잘못된 부분이 있다면 댓글로 알려주시면 수정하도록 하겠습니다 :)

Intro

오늘은 ML/DL 아키텍처, 손실함수(loss function), 미분(derivative), 편미분(partial derivative), ML/DL의 개발 프로세스, Linear/Logistic Regression의 리뷰를 진행했다.
이번 강의에서는 여러 페이지를 번갈아가면서 수업을 진행하여 포스팅 내용의 순서가 매끄럽지 못할 수도 있다.

ML/DL 기본 아키텍처

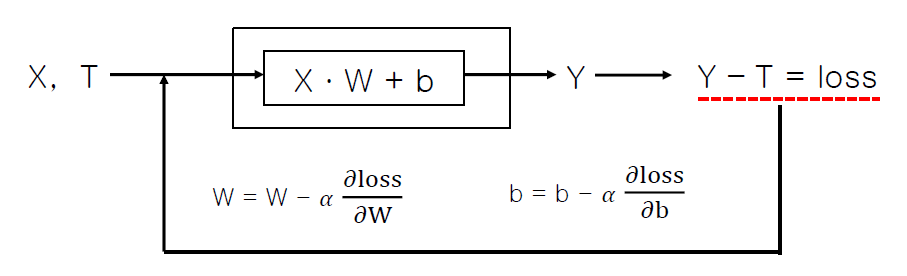모든 ML/DL은 위와 같은 아키텍처를 가진다.
$X, T$는 데이터과 정답, $W, b$는 가중치와 bias, $Y, T$는 기댓값과 정답값, $loss$는 둘의 차이이다.
$X$와 $W$를 대문자로 적은 것은 행렬임을 직관적으로 나타내주는 것이며,
$W=W-\alpha{\partial loss \over \partial W}, b=b-\alpha {\partial loss \over \partial b}$는 $W, b$를 업데이트 시켜주는 과정이라고 보면 된다.

학습(learning) : 계산 값 $Y$와 정답 $T$와의 차이를 나타내는 손실 값(또는 손실함수), $loss$가 최소가 될 때까지 가중치 $W$와 바이어스 $b$를 최적화 시키는 과정.

🔥ML/DL의 궁극적인 목적
주어진 학습 데이터에 대해 손실 함수가 최소가 되는 가중치와 바이어스를 찾는 것

손실함수(loss function)

모든 손실 함수에는 공통점이 2가지 있다.

• 모든 수식에는 $\sum$가 있다.
• 모든 수식에는 $-$가 있다.

GAN의 손실함수에는 $\sum$가 없지 않느냐고 물을 수 있겠지만, $min,max$ 자체가 $\sum$라고 하셨다.

손실 함수는 왜 많을까?
→ Data가 다르므로 동일한 System에서도 결과가 다르다. 따라서 가장 적합한 손실함수를 찾기 위해 다양한 손실 함수가 존재한다.

일반적인 손실함수는 양수이며, 평균을 나타낸다.

미분

$f'(x) = lim_{\Delta x \to 0}{{f(x+\Delta x)- f(x)}\over{}\Delta x}$

미분이 무엇일까?
접선의 기우기? 순간 변화율?

강사님께서 우리는 미분을 데이터 관점으로 들여다볼 필요가 있다고 하셨다.
미분은 입력값이 아주 조금 변하면 출력값이 얼마나 변하는지를 알아내는 과정이라고 하셨다.

여러가지 머신러닝 강의와 책을 보면서 미분에 대하여 자주 들었지만, 한번도 이런 식으로 생각해본 적이 없었다. 그나마 Andrew Ng 교수님의 강의에서 비슷한 내용을 들었던 것 같다.

ML/DL에서 자주 사용되는 함수의 미분

• $f(x)$가 상수일 때 $f'(x) = 0$
• $f(x) = e^x$ → $f'(x) = e^x$

미분 값이 0이라는 것은 $W$를 아무리 변경해도 출력값이 변하지 않는다는 것이고, $e$는 미분해도 자기 자신이라는 것을 알 수 있다.

편미분

편미분은 입력 변수가 하나 이상인 다변수 함수에서 미분하고자 하는 변수 하나를 제외한 나머지 변수들은 상수로 취급하고, 해당 변수를 미분하는 것이다.

Ex) 체중 함수가 '체중(야식, 운동)'처럼 야식/운동의 영향을 받는 2변수 함수라고 가정할 경우, 편미분을 이용하면 각 변수 변화에 따른 체중 변화량을 구할 수 있다.
$\partial 체중 \over \partial 야식$으로 야식이 변하면 체중이 얼마나 변하는지를 알 수 있고, $\partial 체중 \over \partial 운동$으로 운동이 변하면 체중이 얼마나 변하는지 알 수 있다는 것이다.

ML/DL 일반적인 개발 프로세스

0번을 제외하고 1~5번이 딥러닝 과정이다.
여기서 가장 중요한 부분이 바로 1번 부분인데, 실제로 ML/DL 과정에 있어서 가장 시간이 많이 소요되고 어려운 부분이 Data를 처리하는 부분이기 때문이다.
사실 모델 구현하고 하는 부분은 이미 많은 코드들이 있기 때문에 Data를 처리하는 것에 비하면 아무것도 아니다.

여담으로 이전 시간에 설명했듯이 Data⊃AI이기 때문에 Data를 다루는 능력을 기르면 굶어 죽을 일은 없다고 하셨다.

Linear Regression

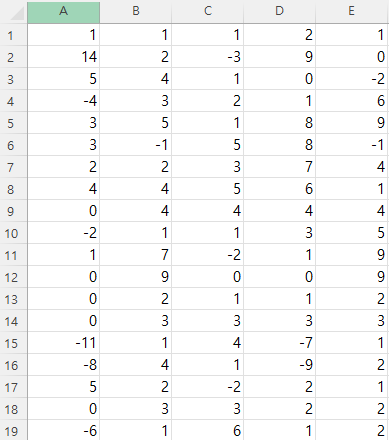다음은 A열이 Label, B~E열이 Data인 scv파일이다.
정답이 continuous value이기 때문에 Linear Regression을 진행해보았다.

위 데이터는 $f(x) = x_1 w_1 + x_2 w_2 + x_3 w_3 + x_4 w_4 +b$로 표현할 수 있다.
여기서 $w$는 정답을 만들어내는 입력데이터의 개수이다.
무슨 이야기냐 하면 1행에서 [1, 1, 2, 1]의 4가지 데이터로 1이라는 정답을 만들어내기 때문에 $w$의 개수 또한 4개가 되는 것이다.

Linear Regression을 통해 $[w_1, w_2, w_3, w_4]$를 구해보면 $[1, -1, 1, -1]$이고, bias는 0인 것을 알 수 있다.

코드를 추가하고 싶지만 글 작성 요령이 없어 글 쓰는 시간이 너무 오래 걸려 어떻게 해야할지 고민이다. 추후에 수정하거나 해야겠다.

Logistic Regression

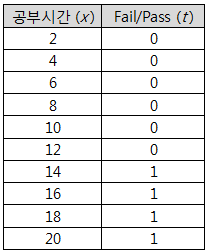위 데이터는 정답이 Discrete value이고 Logistic Regression을 진행해보았다.

Classification은 정답이 연속된 숫자값이 아니기 때문에 activation function을 적용해줘야 하며, 기존 프로세스에서 $Y$와 $loss$가 바뀌게 된다.

activation function을 적용하지 않은 값을 나타내줘도 안될건 없지만 사용자가 '공부시간이 13시간일 때 Pass일 확률이 70%이다.'와 같은 결과를 원할까?
아니면 단순히 '공부시간이 13시간이면 Pass이다.'와 같은 결과를 원할까?

이전 시간에도 설명했지만 사람들은 확실한 것을 좋아한다.
따라서 이러한 수치에 activation function을 적용하는 것이다.

activation function에는 재미있는 점이 한가지 있는데 sigmoid, relu와 같은 activation function은 0에서 1사이의 값을 출력한다.
0~1 사이의 값은 확률값으로 볼 수도 있는데 이러한 이유 덕분에 위에서 설명한 것처럼 'Pass일 확률이 70%이다' 와 같이 쉽게 표현할 수도 있다.

Outro

역시나 글 쓰는 시간이 너무 오래 걸린다...
2시간 가까이 걸렸는데 수업 필기할 때부터 나름 정리한다고 정리해서 작성해놓은 것인데도 글로 다시 옮기려니 시간이 많이 걸린다.
심지어 코드 관련된 내용은 하나도 담지 못했는데 욕심으로는 코드 관련해서도 글에 적고 싶은데 엄두가 안난다.
애초에 필기를 깔끔하게 해서 올리는 것도 고려해봐야겠다.

numpy, 머신러닝 관련 기초를 다시 한번 다지면 좋을 것 같아 이번 주를 이용해서 관련 강의를 들어볼까 한다.
이전에 듣다가 잠깐 Stop 시켜놓은 Andrew Ng 교수님의 Machine learning 수업을 들을까도 고민했는데 일단은 이번 주말까지 정리하는 것이 목표기 때문에 보다 듣기 수월한 강사님의 유튜브 강의를 들을까 한다.