점진적으로 새로운 데이터, 새로운 타겟등이 들어올 예정이다.
이렇게 새로운 데이터를 점진적으로 학습하기 위한 방법을 점진적 학습이라고 한다
점진적 학습의 대표적인 알고리즘으로는 확률적 경사 하강법이 있다
확률적 경사 하강법
우리가 산에서의 어떤 지점에서 내려가기 위해서는, 주변의 내리막길을 찾아, 그곳으로 일정 거리만큼 걸어가면 된다
이때 얼마나 경사를 내려가야할까?
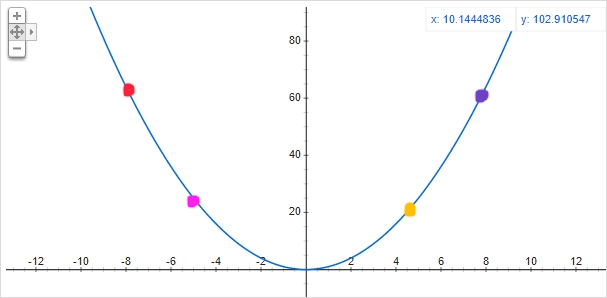
위 그림에서 빨간점을 보자.
미분값을 대략적으로 계산하면 4개의 점중 가장 큰 음수가 나올것이다. 그렇기에 x가 양의 방향으로 크게 움직여야한다.
분홍점은 기울기가 더 작은 음수기에, x가 양의 방향으로 적게 움직인다.
이런식으로 미분 가능한 곡선에서, 미분값을 통하여 x가 움직일 방향과 값을 예측하여 내려간다
그런데!
만약 목적지로 도착하지 못하였다면 어떻게 할까?
이때는 처음부터 다시 내려가기 시작하면 된다. 이 일순을 epoch라고 한다.
미니배치 경사 하강법
그렇게 epoch를 돌려서 어느세월에 다 내려갈까? 그래서 동시에 여러개의 epoch를 수행하는 방법이다
배치 경사 하강법
그것마저 번거로운 작업이라 생각하여, 모든 샘플을 동시에 일순 시키는 방법이다. 하지만 컴퓨터의 자원등을 고려 할 필요가 있다
SGDClassfier
이번에도 데이터를 받아와 특성과 타겟을 분류하여보자
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv_data')
# 특성
fish_input = fish[['Weight','Length','Diagonal','Height','Width']].to_numpy()
# 샘플
fish_target = fish['Species'].to_numpy()
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = \
train_test_split(fish_input, fish_target, random_state=42)
# 스케일 작업
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)이제 epoch를 10번으로 설정하여 모델을 학습시켜보자
from sklearn.linear_model import SGDClassifier
sc = SGDClassifier(loss='log_loss',max_iter=10,tol=None,random_state=42)
sc.fit(train_scaled,train_target)
print_score("iter=10") # score를 찍는 임의의 함수입니다
# 0.78...
# 0.810번으로는 확실히 학습이 부족함을 알 수 있다. 1번만 더 epoch를 돌려보자
sc.partial_fit(train_scaled, train_target)
print_score("iter more")
# 0.831...
# 0.825반복을 많이 하니 점수가 올라갔다. 그럼 얼마나 더 반복이 필요할까?
조기종료
너무 많은 epoch를 순회하면 과대적합의 위험이 있다. 그렇기에 조기종료가 필요하다
import numpy as np
sc = SGDClassifier(loss='log_loss', random_state=42)
train_score = []
test_score = []
classes = np.unique(train_target)
for _ in range(0,300):
sc.partial_fit(train_scaled, train_target, classes=classes)
train_score.append(sc.score(train_scaled, train_target))
test_score.append(sc.score(test_scaled, test_target))
import matplotlib.pyplot as plt
plt.plot(train_score)
plt.plot(test_score)
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()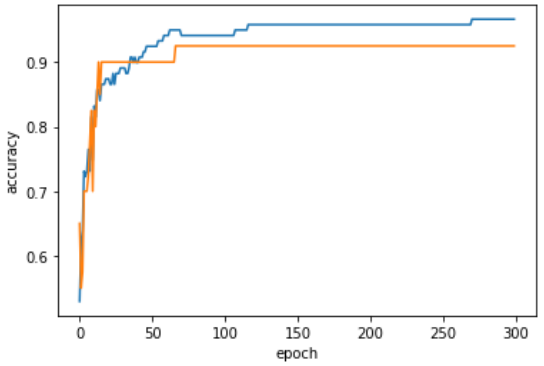
위 그래프를 통해 0~300번까지의 epoch에 따른 점수를 비교해보았다.
확인결과 100번의 epoch 이후 점점 값이 벌어짐을 알 수있고, 적절한 epoch를 100으로 유추 할 수 있다.

