그리디 알고리즘
개념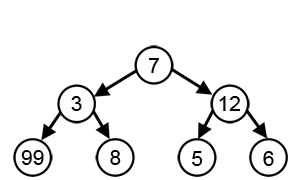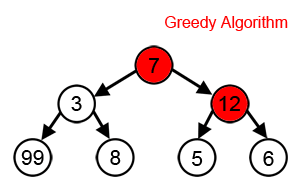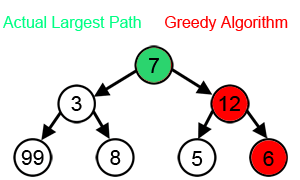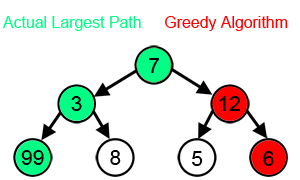
여러 경우 중 하나를 결정해야 할 때 현재 가능한 최선의 옵션을 선택하여 문제를 해결하는 접근 방식. 매 순간 최적의 옵션을 선택하지만, 그 선택의 결과가 항상 최적이라는 보장은 없다.
아래와 같은 특성을 갖고 있는 문제들을 해결할 때 그리디 알고리즘이 사용될 수 있다.
- Greedy Choice Property(탐욕 선택 속성)
한 번 선택하면 이전 단계를 고려하지 않고 각 단계에서 최선의 선택을 함으로써 문제에 대한 최적의 해결책을 찾을 수 있다면, 그리디한 접근 방식을 사용하여 문제를 해결할 수 있다. - Optimal Substructure(최적 부분 구조)
문제 전체에서의 최적해와 하위 문제의 최적해가 일치하는 경우, 매 순간의 최적해를 고르는 것이 곧 문제 전체의 최적해를 고르는 것이기 때문에 그리디 알고리즘이 유용하다.
장점
- 문제 해결 방식이 매우 단순하다.
매 순간 최적의 옵션만을 선택하므로 다른 로직이 필요하지 않다. - 성능이 좋다.
그리디 알고리즘은 최적해를 보장하지 않지만, 어느 정도 유사한 답을 낸다. 정확한 답을 찾는 문제가 아닌 일정 수준의 괜찮은 답을 찾는데 있어서 그리디 알고리즘은 매우 효율적이다. 정확한 답을 내는 타 알고리즘에 비해 빠른 속도로 정답 근사치를 찾을 수 있다.
단점
- 도출한 해가 최적해라는 보장이 없다.
위에서 많이 언급했던 것처럼, 그리디 접근 방식으로 최적해를 정확하게 찾아내기 위해서는 특정 조건이 만족되어야 한다. 그 이야기는 그러한 조건이 만족되지 않는다면 그리디 접근 방식은 최적해를 찾는데 적합하지 않을 가능성이 많다는 의미이다.
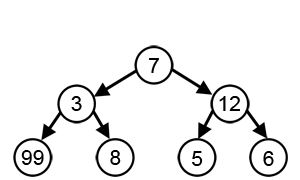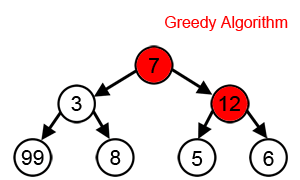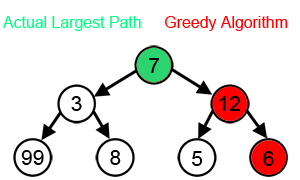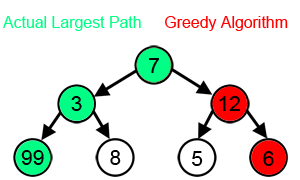그리디 알고리즘이 트리에서 최대 합을 찾는 과정
활용
- Dijkstra 알고리즘
- MST(Minimum Spanning Tree, 최소 신장 트리)
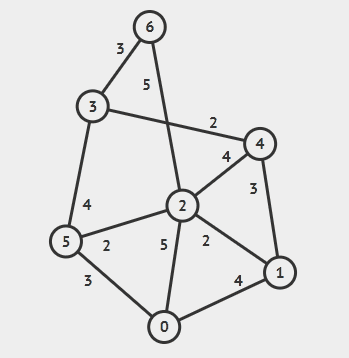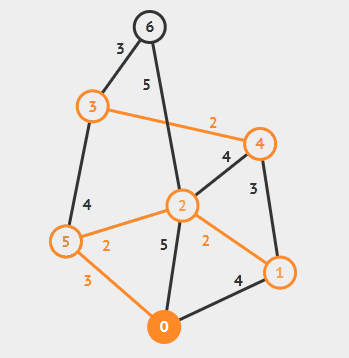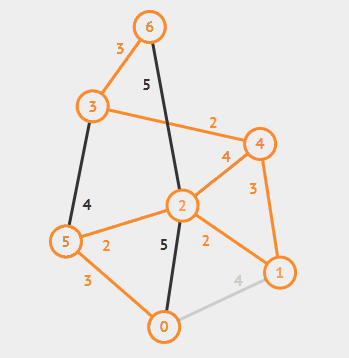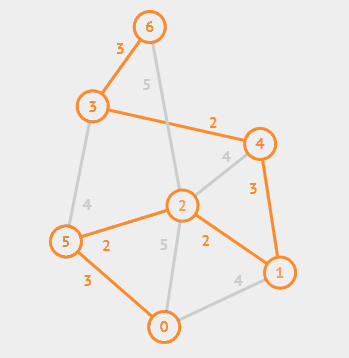
- 거스름돈 문제
- 분할 가능한 배낭 문제
- 선택 정렬
동적 계획법 (Dynamic Programming, DP)
개념
큰 문제를 작은 문제로 나누어 푸는 문제 해결 기법. 복잡한 알고리즘 문제를 하위 문제로 세분화하여 풀고 저장하여, 후에 같은 하위 문제가 나왔을 경우 또 계산하는 대신 저장한 결과를 사용하는 기법이다.
아래와 같은 특성을 갖고 있는 문제들을 해결할 때 DP 알고리즘이 사용될 수 있다.
- Overlaping SubProblems(부분 문제 반복)
동일한 하위 문제가 반복하여 나타나는 경우에 사용 가능하다. DP는 메모이제이션을 통해 한 번 구한 부분 문제의 정답을 저장하고, 같은 부분 문제를 이용할 때에는 저장해 둔 정답을 바로 이용한다. - Optimal Substructure(최적 부분 구조)
그리디 알고리즘과 마찬가지로 작은 문제를 해결함으로써 전체 문제가 해결되어야 한다. 즉, 부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 도출할 수 있는 경우에 DP가 적합하다.
접근 방법
- Top-Down
해결하고자 하는 큰 문제에서 부분 문제로 나누며 기저 상태까지 나뉜 후, 기저 상태의 값을 채우면서 재귀적으로 큰 문제의 최적해를 찾는 방법이다. 재귀적으로 동작하며 내가 원하는 부분 문제만을 호출하므로 불필요한 연산이 적지만, 재귀적 방식이다보니 함수 호출 과정에서 메모리를 많이 사용할 수 있다.
Bottom-Up 방식에 비해 이해하거나 구현하기 쉽다. - Bottom-Up
기저 상태에서부터 그 값을 계산하고, 계산된 결과를 바탕으로 점차 큰 문제에 대한 해답을 구하는 방식이다. 모든 부분 문제의 기저상태부터 출발하며 부분 문제에서 가능한 결과를 모두 계산하고 채우면서 가장 큰 문제까지 도달하기 때문에, 불필요한 연산이 발생할 수 있다. Top-Down 방식에 비해 안정적이다.
다른 알고리즘과 비교
- Divide & Conquer (분할 정복)
- 비슷한 점
- 거대하고 복잡한 문제를 그 문제를 이루는 부분 문제로 나누어, 해결할 수 있는 부분 문제를 해결하면서 전체 문제를 해결한다.
- 분할된 문제는 기존 문제와 성격이 동일하다.
- 다른 점
- 분할 정복 알고리즘은 분할된 문제들이 서로 독립적이다. 분할 정복의 대표적인 활용 사례인 병합 정렬을 생각해보면, 분할된 요소들끼리 어떠한 관계도 갖지 않는다.
- 분할 정복은 단순히 해결하기 어려운 문제를 내가 해결할 수 있는 범위까지 쪼개는 것이 목적이지만, DP는 주어진 문제를 나눌 때 부분 문제를 최대한 많이 활용할 수 있도록 나눈 다음, 부분 문제의 정답을 한 번만 계산하고 그것을 재사용하여 효율성을 높인다.
- 비슷한 점
- Greedy (탐욕)
- 비슷한 점
- 최적 부분 구조의 특성을 가진 문제를 해결하는 데 강점을 가지고 있다.
- 다른 점
- 문제의 정답을 도출하기 위해 그리디 알고리즘은 부분 문제에서 가장 최선의 선택만을 하면서 전체 문제에 대한 정답을 찾아가고, DP는 전체 문제에서 같은 부분 문제가 여러번 사용될 때 부분 문제를 딱 한 번만 계산하고 그 결과를 계속 재사용하며 정답을 찾아간다는 차이점이 있다.
- DP는 정확한 답을 도출하지만 그 과정에서 많은 부분 문제를 계산해야 한다. 그리디는 각 과정에서 최선의 선택을 하면서 문제를 해결하기 때문에 수행 시간이 빠르지만 구한 답이 최적해가 아닐 수 있다.
- 비슷한 점
장점
- 반복되는 과정(재귀)이 많으면 많을 수록 효율성이 상승한다.
피보나치 5번째 값을 구하는 재귀 과정
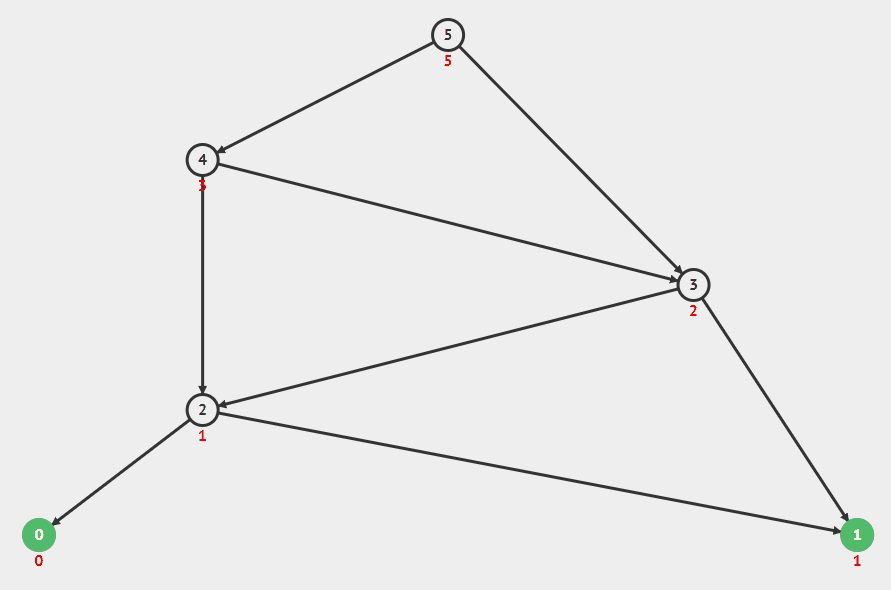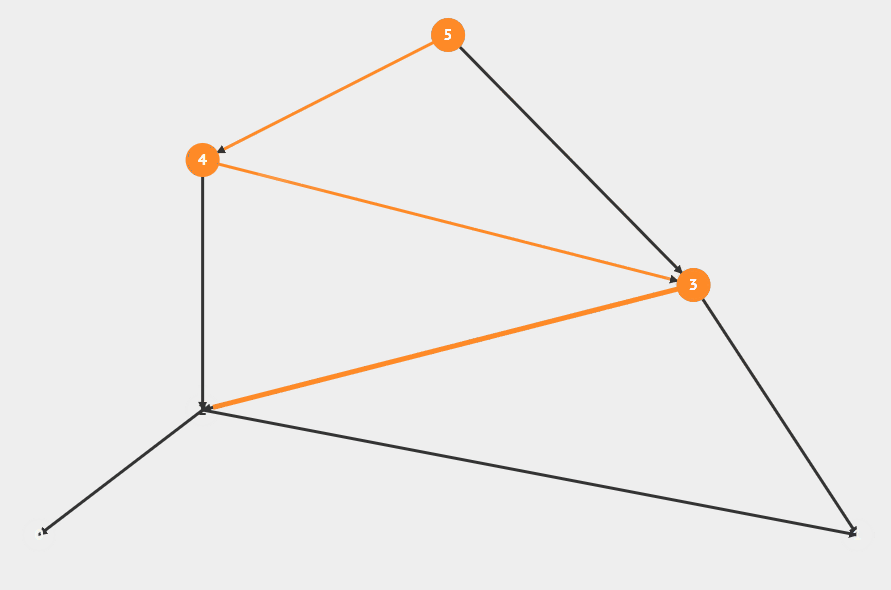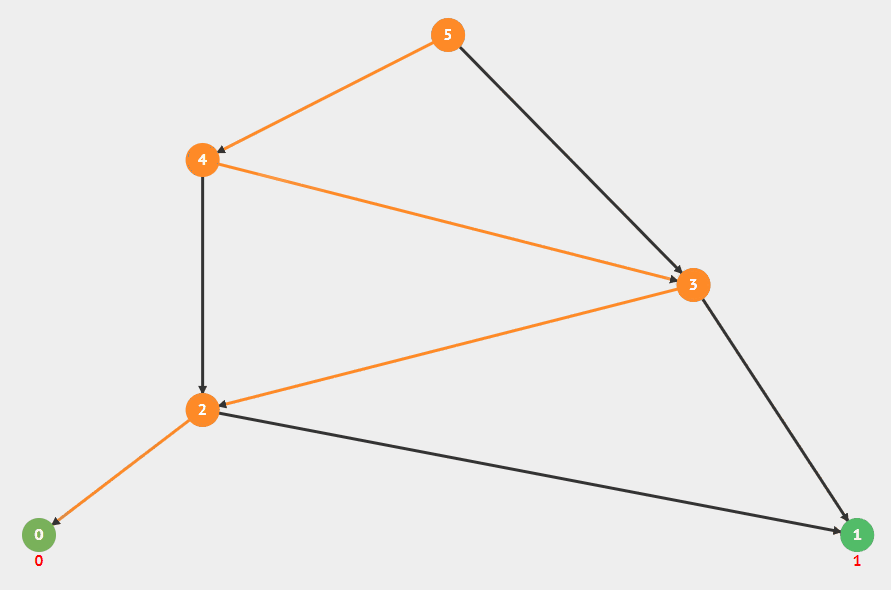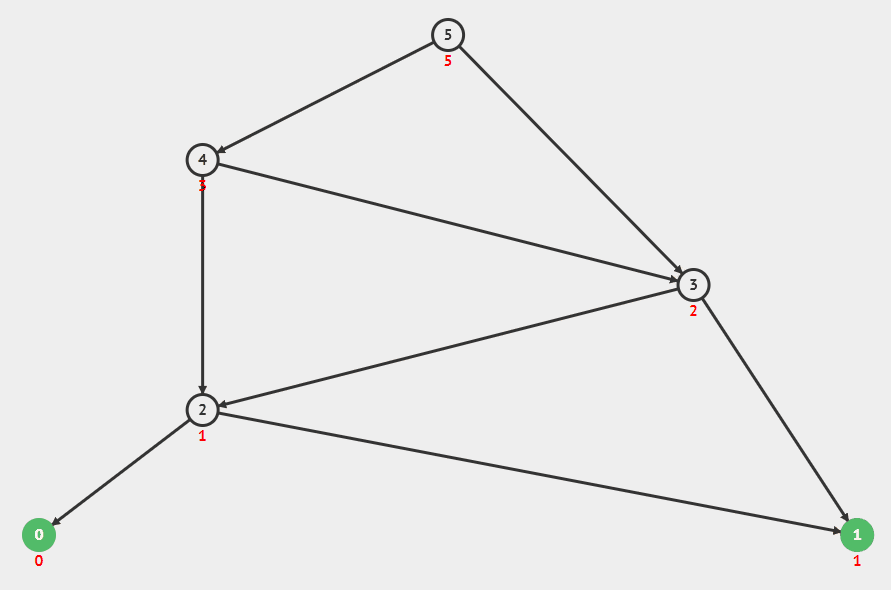
피보나치 5번째 값을 구하는 DP 과정
- 구체적인 알고리즘이라기 보다는 문제해결 패러다임에 가깝기 때문에 다른 알고리즘과 결합하여 효율적인 문제 해결을 위해 사용할 수 있다.
단점
- 특정한 조건(부분 문제 반복, 최적 부분 구조)을 만족하지 않는 문제인 경우 사용하기 힘들다.
- 다른 알고리즘과 결합하여 사용할 수 있는 만큼, DP에 대한 이해가 부족하면 활용하기 어렵다.
- 부분 문제의 결과를 저장할 공간이 필요하기 때문에 메모리의 사용량이 많다.
활용
- LIS
- 피보나치 수열
- 0-1 배낭 문제
- 외판원 순회
- Bellman-Ford, Floyd-Warshall 알고리즘
- 많은 재귀적 문제
기억은 유한, 기록은 무한